K-means聚类算法

 

一、K-means聚类算法简介

K-means算法是典型的基于距离的聚类算法，即对各个样本集采用距离作为相似性的评价指标，若两个样本集的距离越近，其相似度就越大。按照样本之间的距离大小，将样本集划分为K个簇。让簇内的点尽量紧密的连在一起，且让簇间的距离尽量的大。最后把得到紧凑且独立的簇作为最终的目标。

 

二、相关知识点

1、距离度量：不同的距离量度会对距离的结果产生影响，常见的距离量度公式有很多。在该算法中一般采用欧几里得公式：

 

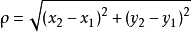
其中， 为点与点之间的距离；

但是欧几里得距离度量会受指标不同单位刻度的影响，所以一般需要先进行标准化。距离越大，个体间差异越大；

2、聚类分析：聚类分析是在数据中发现数据对象之间的关系，将数据进行分组，组内的相似性越大，组间的差别越大，则聚类效果越好。

3、簇类型：用不同的簇类型划分数据的结果是不同的，簇的类型有很多种。如：

   3.1 基于中心的簇。就是每个点到其簇的距离比到任何其他簇的距离都近，这是最常见也是K-means聚类算法优先选择的簇类型。

   3.2 分离明显的簇。即每个点到其簇中任意一个点的距离都小于到不同簇中的其他点的距离。

   3.3 基于密度的簇。簇是被低密度区域分开的高密度区域。

   3.4 概念簇。簇中的点具有由整个点集导出的某种共同的性质。

 

三、K-means算法过程

  （1）随机选取K个初始质心

（2）分别计算所有样本到这K个质心的距离

（3）如果样本离某质心Ki最近，那么这个样本属于Ki点群；如果到多个质心的距离相等，则可划分到任意组中

（4）按距离对所有样本分完组之后，计算每个组的均值（最简单的方法就是求样本每个维度的平均值），作为新的质心

（5）重复（2）（3）（4）直到新的质心和原质心相等，算法结束

 

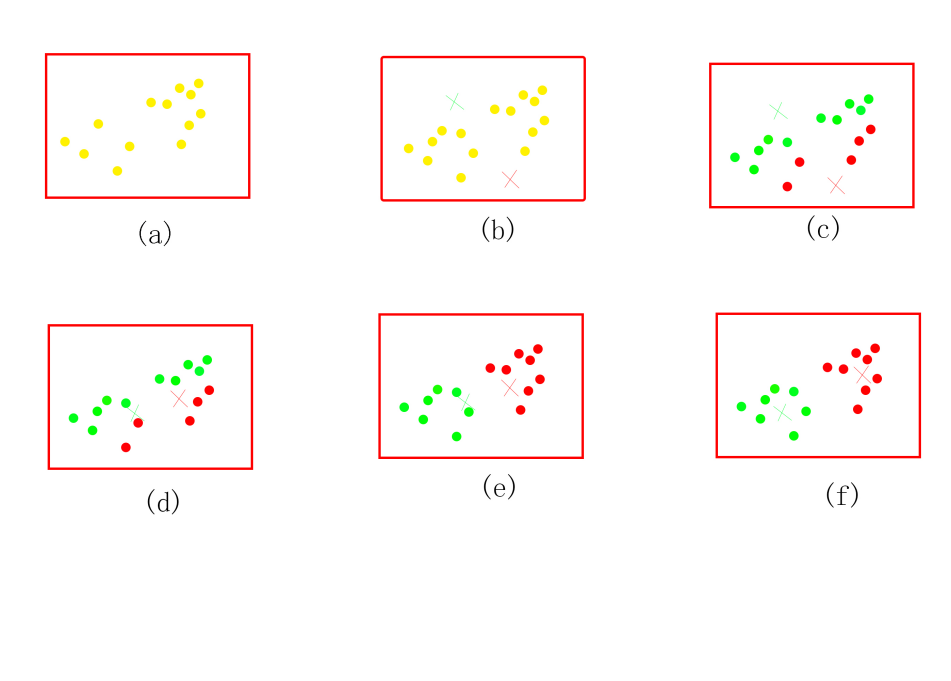
如上图所示，图a表达了初始的样本集，假设质心k=2。（上图中用红色×和绿色×表示两个不同的质心）在图b中随机选择两个k类所对应的类别质心，即图中的红色质心和绿色质心，然后分别求样本中所有点到这两个质心的距离，并标记每个样本的类别为和该样本距离最小的质心的类别，如图c所示，经过计算样本和红色质心和绿色质心的距离，我们得到了所有样本点的第一轮迭代后的类别。此时我们对我们当前标记为红色和绿色的点分别求其新的质心，如图d所示，新的红色质心和绿色质心的位置已经发生了变动。图e和图f重复了我们在图c和图d的过程，即将所有点的类别标记为距离最近的质心的类别并求新的质心。最终我们得到的两个类别如图f。

在实际K-Means算法中，多次运行图c和图d会达到最终的更优的类别。

 

四、代码实现

    实验中给定质心数量K值为2，样本数据为 { 3.0, 9.0 }, { 2.0, 6.0 }, { 8.0, 4.0 }, { 7.0, 9.0 }, {6.0,5.0}, { 8.0, 4.0 }, { 10.0, 2.0 }, { 4.0, 9.0 }, { 8.0, 3.0 }, { 2.0, 3.0 }, {3.0,9.0}

  运行结果：

 

 

 

 

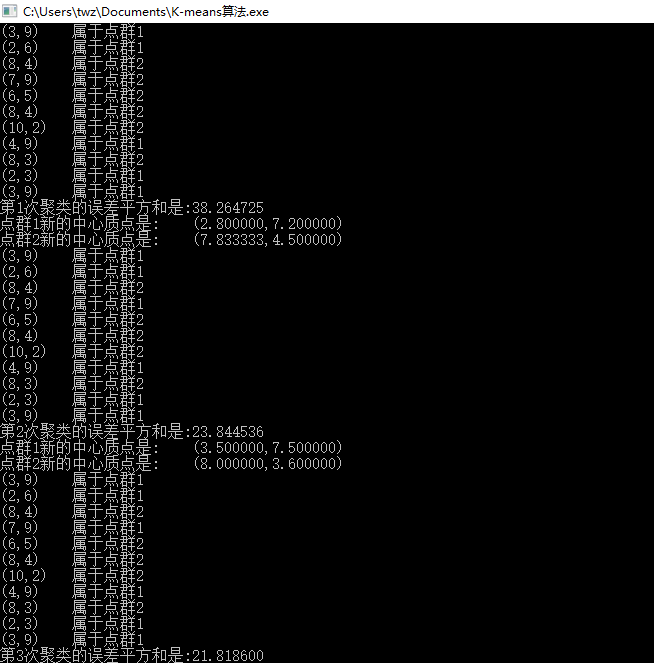
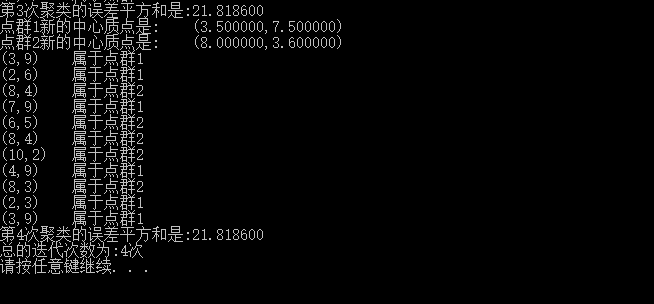
完整代码如下：

#include"stdio.h"
#include"stdlib.h"
#include"math.h"
#include<iostream>
using namespace std;

#define N 11
#define k 2

typedef struct{
    float x;
    float y;
}Point;

Point point[N] = {
        { 3.0, 9.0 }, { 2.0, 6.0 }, { 8.0, 4.0 }, { 7.0, 9.0 }, {6.0,5.0},
        { 8.0, 4.0 }, { 10.0, 2.0 }, { 4.0, 9.0 }, { 8.0, 3.0 }, { 2.0, 3.0 }, {3.0,9.0}
};

int center[N];
Point mean[k];

float getdistance(Point point1, Point point2);
void cluster();
float gete();
void getmean(int center[N]);

int main()
{
    //初始化k个中心点,这里选择给定中心点，而不是随机生成，需要更多的先验知识
    //若没有相关先验知识，可选择随机生成初始中心点
    mean[0].x = point[0].x;
    mean[0].y = point[0].y;

    mean[1].x = point[3].x;
    mean[1].y = point[3].y;

    mean[2].x = point[6].x;
    mean[2].y = point[6].y;
    int number=0;
    float temp1, temp2;
    //第一次聚类
    cluster();
    number++;//number统计进行了几次聚类
    //对第一次聚类的结果进行误差平方和的计算   
    temp1 = gete();
    printf("第1次聚类的误差平方和是:%f\n", temp1);
    //针对第一次聚类的结果，重新计算聚类中心
    getmean(center);
    //第二次聚类
    cluster();
    number++;
    temp2 = gete();
    printf("第2次聚类的误差平方和是:%f\n", temp2);

    //迭代循环，直到两次迭代误差的差值在一定阈值范围内，则迭代停止
    while (fabs(temp1 - temp2) > 0.5)
    {
        temp1 = temp2;
        getmean(center);
        cluster();
        temp2 = gete();
        number++;
        printf("第%d次聚类的误差平方和是:%f\n", number,temp2);
    }
    printf("总的迭代次数为:%d次\n", number);

    system("pause");
    return 0;

}

//计算距离函数，欧式距离
float getdistance(Point point1, Point point2)
{
    float d;
    d = sqrt((point1.x - point2.x)*(point1.x - point2.x) + (point1.y - point2.y)*(point1.y - point2.y));
    return d;
}
//聚类函数
void cluster()
{
    float distance[N][k];
    for (int i = 0; i < N; i++)
    {
        for (int j = 0; j < k; j++)
        {
            distance[i][j] = getdistance(point[i], mean[j]);
        }
        float min = 9999.0;
        for (int j = 0; j < k; j++)
        {
            if (distance[i][j] < min)
            {
                min = distance[i][j];
                center[i] = j;
            }
        }
        printf("(%.0f,%.0f)\t 属于点群%d\n", point[i].x, point[i].y, center[i] + 1);
    }
}
//聚类后误差计算函数
float gete()
{
    float cnt=0, sum=0;
    for (int i = 0; i < N; i++)
    {
        for (int j = 0; j < k; j++)
        {
            if (center[i] == j)
            {
                cnt = getdistance(point[i], mean[j]);
            }
        }
        sum += cnt;     
    }
    return sum;
}

//重新计算聚类中心
void getmean(int center[N])
{
    Point sum;
    int count;
    for (int i = 0; i < k; i++)
    {
        sum.x = 0.0;
        sum.y = 0.0;
        count = 0;
        for (int j = 0; j < N; j++)
        {
            if (center[j] == i)
            {
                sum.x += point[j].x;
                sum.y += point[j].y;
                count++;
            }
        }
        mean[i].x = sum.x / count;
        mean[i].y = sum.y / count;
    }
    for (int i = 0; i < k; i++)
    {
        printf("点群%d新的中心质点是:\t(%f,%f)\n", i + 1, mean[i].x, mean[i].y);
    }
}

 

五、总结

1、对于K-Means算法，首先要注意的是k值的选择，即簇数的选择。上个例子中我对k值选择是随机选择的，对如何选择一个合适的k值还不清楚！后面会继续学习，也希望有知道的同学给予建议

2、当确定了k值后，我们需要选择k个初始化的质心，就像上图b中的红色质心和绿色质心。质心的确定也是随机选择的。值得注意的是k个初始化的质心的位置的选择对最后的聚类结果和运行时间都有很大的影响，所有选择合适的质心很重要，我个人总结的结论是这些质心最好不能隔太近，另外根据实际情况选择合适的迭代次数也很重要。

3、算法实现比较容易，原理也比较简单，调度参数主要是簇数k值和迭代次数。、

 

六、算法优化方案

      通过实验可知，质心位置的选择对最后的聚类结果和运行时间都有很大的影响，因此需要选择合适的k个质心。如果完全随机的选择，就很有可能导致算法低效。通过上网查阅相关资料得知，K-Means++算法是对K-Means随机初始化质心的方法的优化。

K-Means++算法如下：

　　　　（1)从输入的数据点集合中随机选择一个点作为第一个聚类中心μ1
　　　　 (2)对于数据集中的每一个点xi，计算它与已选择的聚类中心中最近聚类中心的距离D（xi）

　　　　 (3)选择一个新的数据点作为新的聚类中心，选择的原则是：D(x）较大的点，被选取作为聚类中心的概率较大
　　　　 (4)重复(2)和(3直到选择出k个聚类质心
　　　　 (5)利用这k个质心来作为初始化质心去运行标准的K-Means算法

 

 

参考网站：https://baike.so.com/doc/6953641-7176056.html

         https://blog.csdn.net/code_caq/article/details/68486668