机器学习实战-AdaBoost

1.概念

从若学习算法出发，反复学恶习得到一系列弱分类器(又称基本分类器)，然后组合这些弱分类器构成一个强分类器。简单说就是假如有一堆数据data，不管是采用逻辑回归还是SVM算法对当前数据集通过分类器data进行分类，假如一些数据经过第一个分类器之后发现是对的，而另一堆数据经过第一个分类器之后发现数据分类错了，在进行下一轮之前就可以对这些数据进行修改权值的操作，就是对上一轮分类对的数据的权值减小，上一轮分类错的数据的权值增大。最后经过n个分类器分类之后就可以得到一个结果集

注意：adaboost算法主要用于二分类问题，对于多分类问题，adaboost算法效率在大多数情况下就不如随机森林和决策树

要解决的问题：如何将弱分类器(如上描述每次分类经过的每个分类器都是一个弱分类器)组合成一个强分类器：加大分类误差小的瑞分类权值减小分类误差大的弱分类器权值

1.1举例分析

2.决策树，随机森林,adaboost算法比较

以乳腺癌为例来比较三种算法

2.1 加载数据

#使用train_test_split将数据集拆分
from sklearn.model_selection import train_test_split
#将乳腺癌的数据导入，return这个参数是指导入的只有乳腺癌的数据
#如果没有参数，那么导入的就是一个字典，且里面有每个参数的含义
X,y=datasets.load_breast_cancer(return_X_y=True)
#测试数据保留整个数据集的20%
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size= 0.2)

2.2使用决策树

score=0
for i in range(100):  
    model=DecisionTreeClassifier()
    #将训练集数据及类别放入模型中
    model.fit(X_train,y_train)
    y_ =model.predict(X_test)#预测测试集里的数据类型
    score+=accuracy_score(y_test,y_)/100
print("多次执行，决策树准确率是：",score)

运行结果

2.3随机森林

score=0
for i in range(100):
    #随机森林的两种随机性：一种是随机抽样，另一种是属性的随机获取。而决策树只有随机抽样一种随机性
    model=RandomForestClassifier()
    #将训练集数据及类别放入模型中
    model.fit(X_train,y_train)
    y_ =model.predict(X_test)#预测测试集里的数据类型
    score+=accuracy_score(y_test,y_)/100
print("多次执行，随机森林的准确率为是：",score)

2.4adaboost自适应提升算法

score=0
for i in range(100):
    model=AdaBoostClassifier()
    #将训练集数据及类别放入模型中
    model.fit(X_train,y_train)
    y_ =model.predict(X_test)#预测测试集里的数据类型
    score += accuracy_score(y_test,y_)/100
print("多次执行，adaboost准确率是：",score)

3.手撕算法

adaboost三轮计算结果

在代码中的体现就是X[i]的值

import numpy as np
from sklearn.ensemble import AdaBoostClassifier

from sklearn import tree
import graphviz
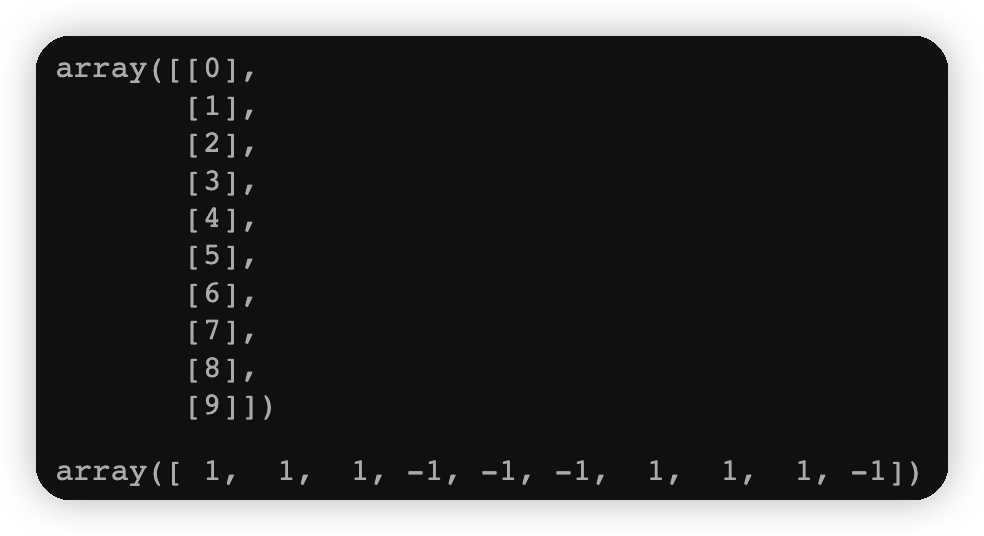
X=np.arange(10).reshape(-1,1)#二维，机器学习要求数据必须是二维的

y=np.array([1,1,1,-1,-1,-1,1,1,1,-1])
display(X,y)

display(X,y)运行结果如下图

# SAMME表示构建树的时候，采用相同的裂分方式
#n_estimators表示分裂为三颗树
model = AdaBoostClassifier(n_estimators=3,algorithm='SAMME')
model.fit(X,y)
y_=model.predict(X)

第一颗树的可视化

dot_data=tree.export_graphviz(model[0],filled=True,rounded=True)
graphviz.Source(dot_data)

运行结果

第二棵树的可视化

dot_data=tree.export_graphviz(model[1],filled=True,rounded=True)
graphviz.Source(dot_data)

第三课树的可视化

dot_data=tree.export_graphviz(model[2],filled=True,rounded=True)
graphviz.Source(dot_data)

3.1第一轮

3.1.2gini系数的计算

此处计算的X[i]的值也就是v的值

w1=np.full(shape=10,fill_value=0.1)#初始的样本权重

cond=y ==1 #类别1条件

p1 = w1[cond].sum()
p2= 1-p1
display(p1,p2)

gini=p1*(1-p1)+p2*(1-p2)

上图可知第一棵树的X[0]=2.5的由来方式如下代码如实现

gini_result=[]
best_split={}#最佳分裂条件，X[0]<=2.5
lower_gini = 1#比较
for i in range(len(X)-1):#数组下标从0到9，10个数据一共要切九刀
    split=X[i:i+2].mean()#裂开条件，就是假如一开始要将0和1裂开并取出
    cond=(X<=split).ravel()#变成一维的，左边数据
    left=y[cond]
    right=y[~cond]#取反
    
    #左右两边的gini系数
    gini_left=0
    gini_right=0
    for j in np.unique(y):#y表示类别
        p_left=(left==j).sum()/left.size#计算左边某个类别的概率
        gini_left=p_left*(1-p_left)
        p_right=(right==j).sum()/right.size#计算右边某个类别的概率
        gini_right=p_right*(1-p_right)
        
    #左右两边的gini系数合并
    left_p=cond.sum()/cond.size
    right_p=1-left_pc
    
    gini=gini_left*left_p + gini_right*right_p
    gini_result.append(gini)
    if gini <lower_gini:
        lower_gini=gini
        best_split.clear()
        best_split['X[0]<=']=split
print(gini_result)
print(best_split)

3.1.3求误差

y1_=model[0].predict(X)#由v得到的预测结果小于v为1，大于v为-1

error1=(y!=y1_).mean()#求出预测值与实际值不相等元素的个数，并求平均

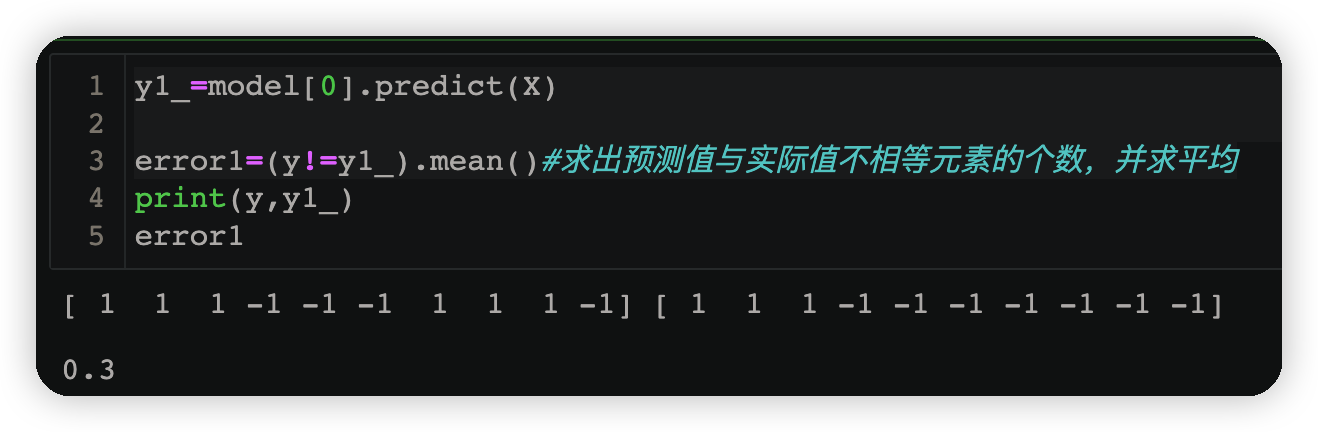
3.1.4计算第一个若学习器的权重

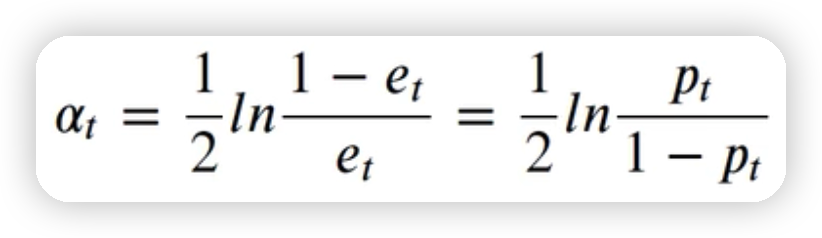
alpha_1=1/2*np.log((1-error1)/error1)

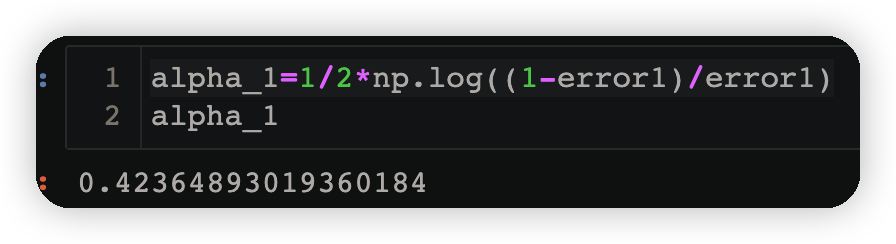
3.1.5 跟新样本权重

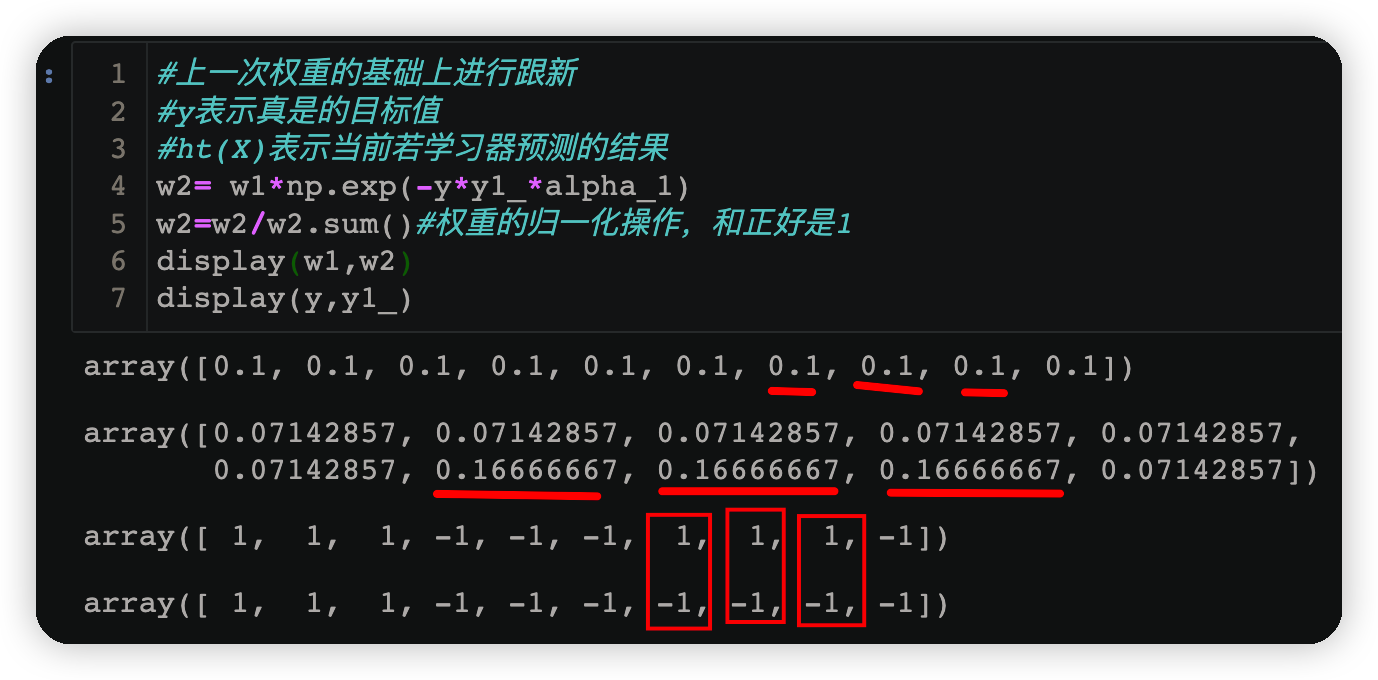
#上一次权重的基础上进行跟新
#y表示真是的目标值
#ht(X)表示当前若学习器预测的结果
w2= w1*np.exp(-y*y1_*alpha_1)
w2=w2/w2.sum()#权重的归一化操作，和正好是1
display(w1,w2)
display(y,y1_)

由下方运行结果可知当预测结果与原数据不相同时，该样本对应的权值也会随之增大；反之若预测正确则权值会减小

3.2第二轮的计算

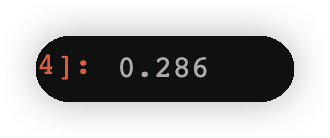
也即第二课数的计算

cond=y==-1
np.round(w2[cond].sum(),3)#找到类别为-1的所有权值的和，四舍五入保留3位小数

cond2=y==1
np.round(w2[cond2].sum(),3)

3.2.1 gini系数的计算

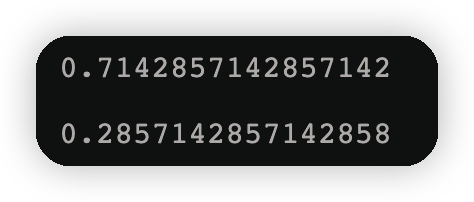
cond=y ==1 #类别1条件

p1 = w2[cond].sum()#使用新的样本权重分布
p2= 1-p1
display(p1,p2)

gini=p1*(1-p1)+p2*(1-p2)

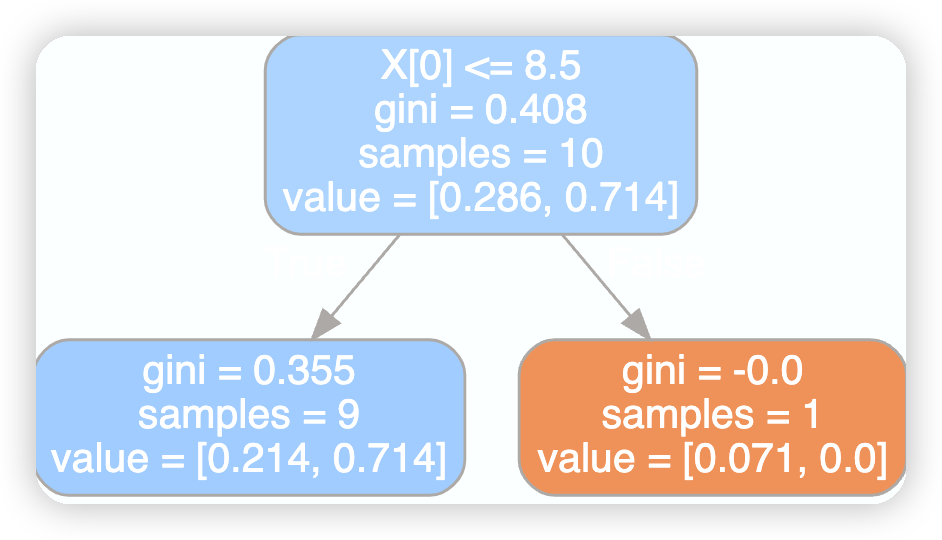
3.2.2拆分的条件

gini_result=[]
best_split={}#最佳分裂条件，X[0]<=8.5
lower_gini = 1#比较
for i in range(len(X)-1):#数组下标从0到9，10个数据一共要切九刀
    split=X[i:i+2].mean()#裂开条件，就是假如一开始要将0和1裂开并取出
    cond=(X<=split).ravel()#变成一维的，左边数据
    left=y[cond]
    right=y[~cond]#取反
    
     #left_p=cond.sum()/cond.size#这种方式计算概率适用于每个样本的权重一样
    left_p = w2[cond]/w2[cond].sum()#归一化，左侧每个样本在自己组内的概率
    right_p=w2[~cond]/w2[~cond].sum()#归一化，右侧每个样本在自己组内概率
    
    #左右两边的gini系数
    gini_left=0
    gini_right=0
    for j in np.unique(y):#y表示类别
        cond_left=left==j#左侧某个类别
        p_left=left_p[cond_left].sum()#计算左边某个类别的概率
        gini_left += p_left*(1-p_left)
        
        cond_right=right==j#右侧某个类别
        p_right=right_p[cond_right].sum()#计算右边某个类别的概率
        gini_right += p_right*(1-p_right)
        
    #左右两边的gini系数合并
    p1=cond.sum()/cond.size#左侧划分数据所占的比例
    p2=1-p1#右侧划分数据所占的比例
    
    gini=gini_left*p1 +gini_right*p2
    gini_result.append(gini)
    if gini <lower_gini:
        lower_gini=gini
        best_split.clear()
        best_split['X[0]<=']=split
print(gini_result)
print(best_split)

3.2.3计算误差

y2_ = model[1].predict(X)#根据求出来的v得到预测的结果

error2=((y != y2_)*w2).sum()
error2

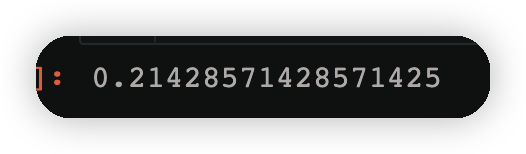
3.2.4计算第二个弱学习器权重

alpha_2=1/2*np.log((1-error2)/error2)
alpha_2

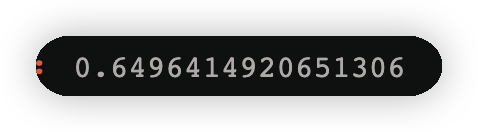
3.2.5跟新样本权重

#上一次权重的基础上进行更新
#y表示真是的目标值
#ht(X)表示当前若学习器预测的结果
w3= w2*np.exp(-y*y2_*alpha_2)
w3=w3/w3.sum()#权重的归一化操作，和正好是1
display(w2,w3)
display(y,y2_)

3.3第三轮计算

3.3.1 gini系数

cond=y ==1 #类别1条件

p1 = w3[cond].sum()#使用新的样本权重分布
p2= 1-p1
display(p1,p2)

gini=p1*(1-p1)+p2*(1-p2)
gini

3.3.2拆分条件

gini_result=[]
best_split={}#最佳分裂条件，X[0]<=2.5
lower_gini = 1#比较
for i in range(len(X)-1):#数组下标从0到9，10个数据一共要切九刀
    split=X[i:i+2].mean()#裂开条件，就是假如一开始要将0和1裂开并取出
    cond=(X<=split).ravel()#变成一维的，左边数据
    left=y[cond]
    right=y[~cond]#取反
    
     #left_p=cond.sum()/cond.size#这种方式计算概率适用于每个样本的权重一样
    left_p = w3[cond]/w3[cond].sum()#归一化，左侧每个样本在自己组内的概率
    right_p=w3[~cond]/w3[~cond].sum()#归一化，右侧每个样本在自己组内概率
    
    #左右两边的gini系数
    gini_left=0
    gini_right=0
    for j in np.unique(y):#y表示类别
        cond_left=left==j#左侧某个类别
        p_left=left_p[cond_left].sum()#计算左边某个类别的概率
        gini_left += p_left*(1-p_left)
        
        cond_right=right==j#右侧某个类别
        p_right=right_p[cond_right].sum()#计算右边某个类别的概率
        gini_right += p_right*(1-p_right)
        
    #左右两边的gini系数合并
    p1=cond.sum()/cond.size#左侧划分数据所占的比例
    p2=1-p1#右侧划分数据所占的比例
    
    gini=gini_left*p1 +gini_right*p2
    gini_result.append(gini)
    if gini <lower_gini:
        lower_gini=gini
        best_split.clear()
        best_split['X[0]<=']=split
print(gini_result)
print(best_split)

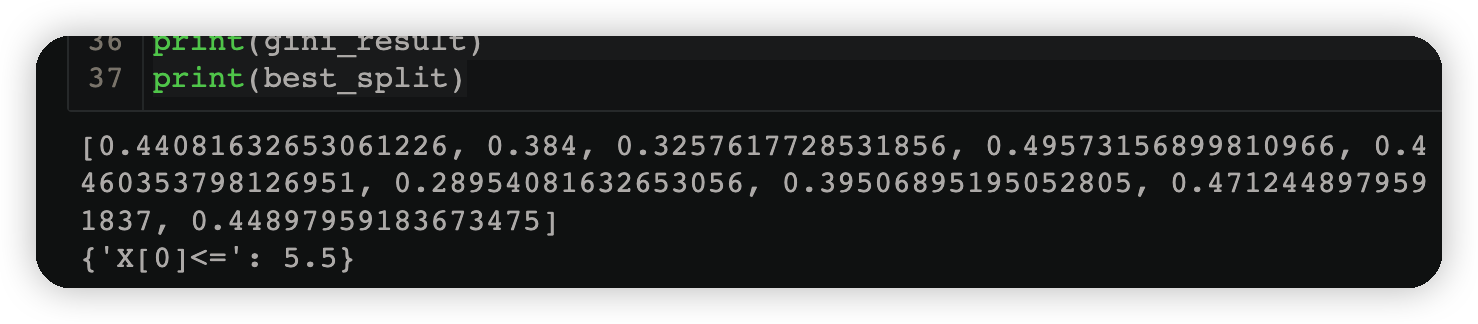
3.3.3计算误差

y3_ = model[2].predict(X)#根据求出来的v得到预测的结果

error3=((y != y3_)*w3).sum()
error3

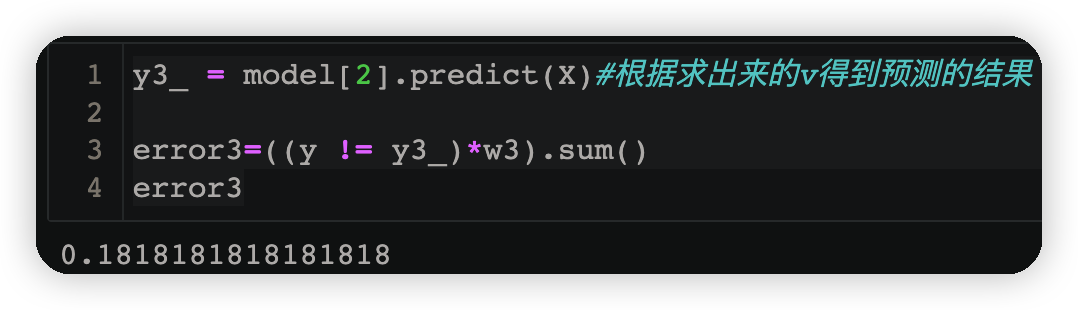
3.3.4计算第三个弱学习器权重

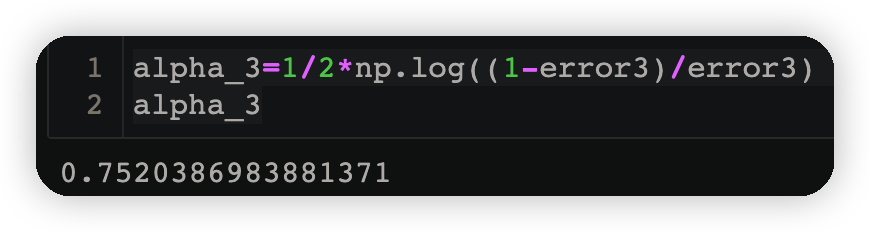
alpha_3=1/2*np.log((1-error3)/error3)
alpha_3

3.3.5跟新权重

#上一次权重的基础上进行更新
#y表示真是的目标值
#ht(X)表示当前若学习器预测的结果
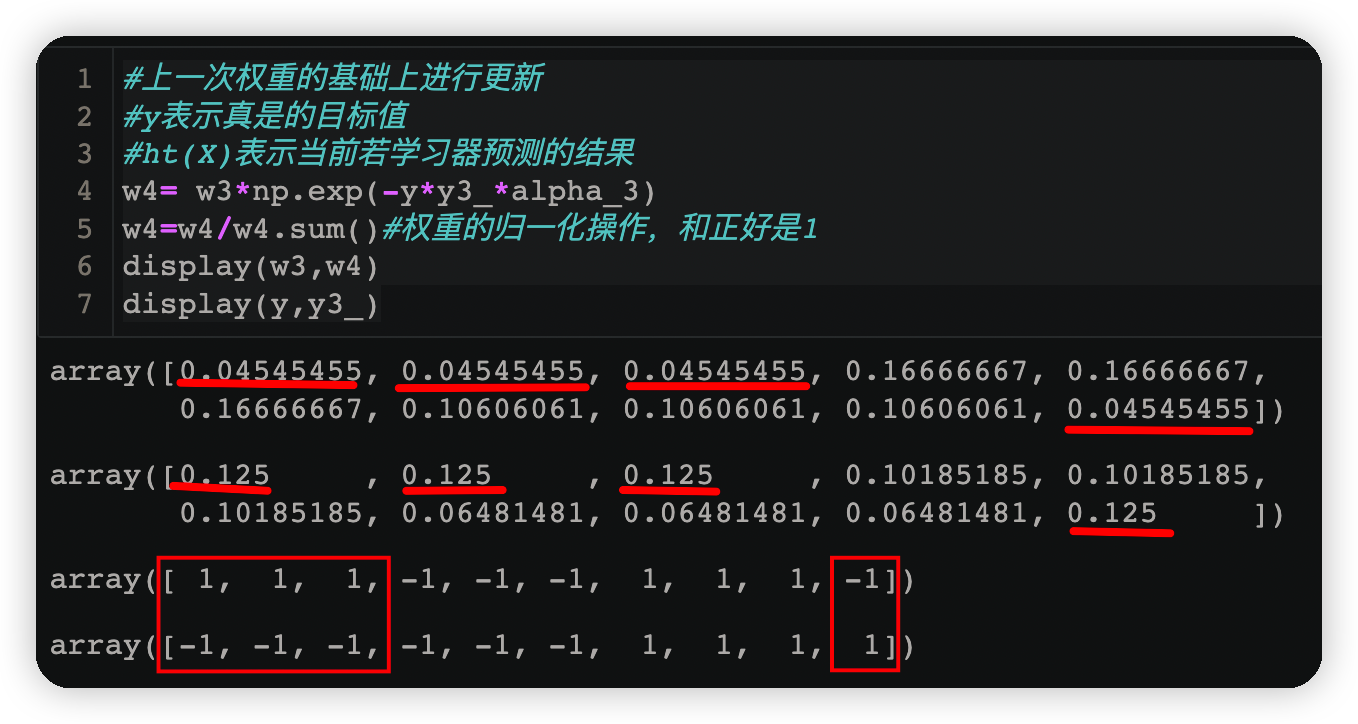
w4= w3*np.exp(-y*y3_*alpha_3)
w4=w4/w4.sum()#权重的归一化操作，和正好是1
display(w3,w4)
display(y,y3_)

3.4弱学习器的聚合

print("每一个弱分类器的预测结果：")
display(y1_,y2_,y3_)
#F 表示聚合各个弱学习器的评分
F=alpha_1*y1_ + alpha_2*y2_ + alpha_3*y3_
#将多个弱分类器，整合，变成了强分类器F(X)
print("强分类器合并结果：\n",F)
#根据得到的最终的F,如果i大于0就是1，否则就是-1，就像把最终的结果放进符号函数中
print("强分类器最终结果如下：\n",np.array([1 if i > 0 else -1 for i in F]))

print("算法预测结果为：\n",model.predict(X))