andrew ng machine learning week5 神经网络

吴恩达机器学习全套笔记博客地址

week 1 

week 2 

week 3 

week 4

week 5

week 6 

week 7

week 8

week 9

 

GitHub 地址

cost function

L ： 网络层数

Sl : 某一层的单元个数

二分类: 仅有一个输出单元，0/1

多分类：K维输出向量，其中为1的维度即为预测分类的类别

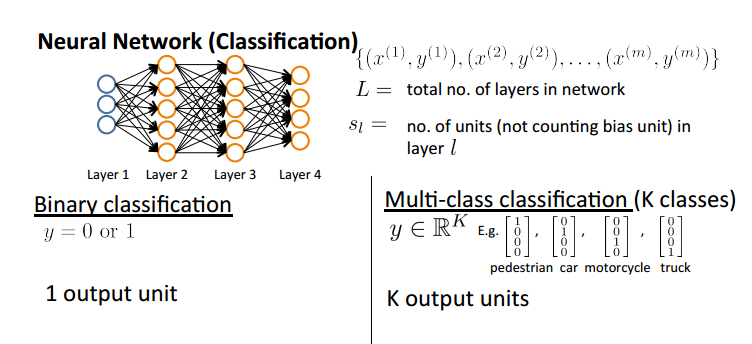
 神经网络为K个输出的求和，并且正则化项依旧不含bias项 

 

反向传播算法 

要使用梯度下降法使代价函数最小，我们要编写代价函数和偏导项的代码，接下来的问题探讨如何利用反向传播算法计算偏导项：

 

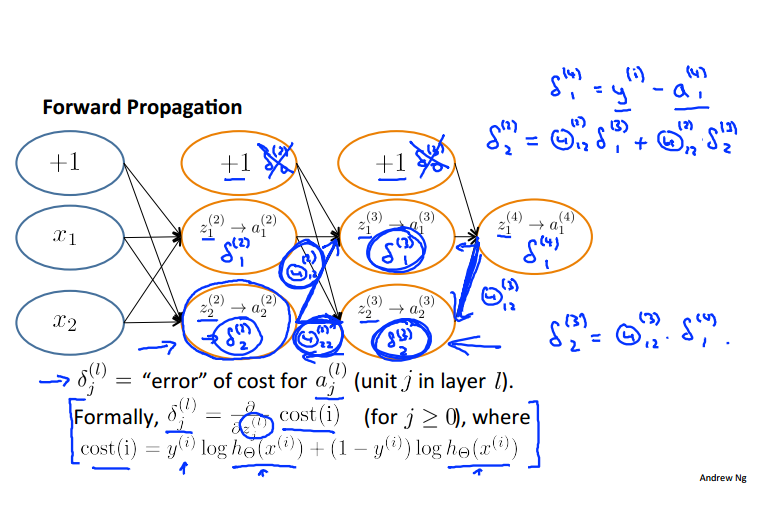
 给定一个训练样本，我们计算前向传播的激励值的方法是：

反向传播计算激励值对应的误差项的方法：

最终的反向传播计算偏导：

1. 初始化△

2. 进行m次循环，每次循环中，首先输入样本x,通过前向算法计算每层的激励值（一个向量），再使用反向传播算法倒着计算每层的δ误差（和α同维度的向量）

3. △是个矩阵（这一块有些不太理解）

4. 根据是否是bia term计算偏导数D

完全版：

反向传播的深入理解

 

实际的应用方法 unroll parameters 

 

 

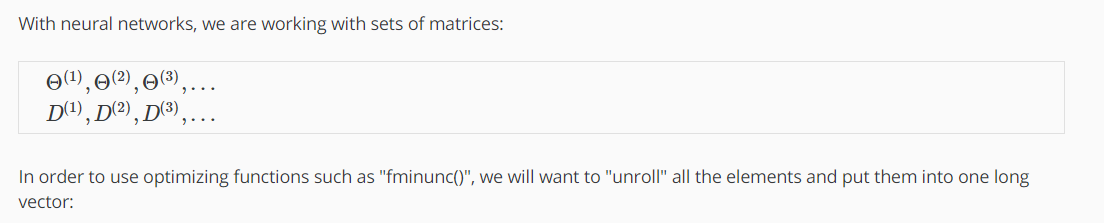
thetaVector = [ Theta1(:); Theta2(:); Theta3(:); ]
deltaVector = [ D1(:); D2(:); D3(:) ]

 

If the dimensions of Theta1 is 10x11, Theta2 is 10x11 and Theta3 is 1x11, then we can get back our original matrices from the "unrolled" versions as follows:

Theta1 = reshape(thetaVector(1:110),10,11)
Theta2 = reshape(thetaVector(111:220),10,11)
Theta3 = reshape(thetaVector(221:231),1,11)

算法过程：

1. 初始化的三个参数，进行展开成为initialdata 

2. 在costfunction函数中reshape得到参数θ计算D，最后展开成为长向量gradientvec

gradientchecking 梯度检验

数值化的梯度计算方法：

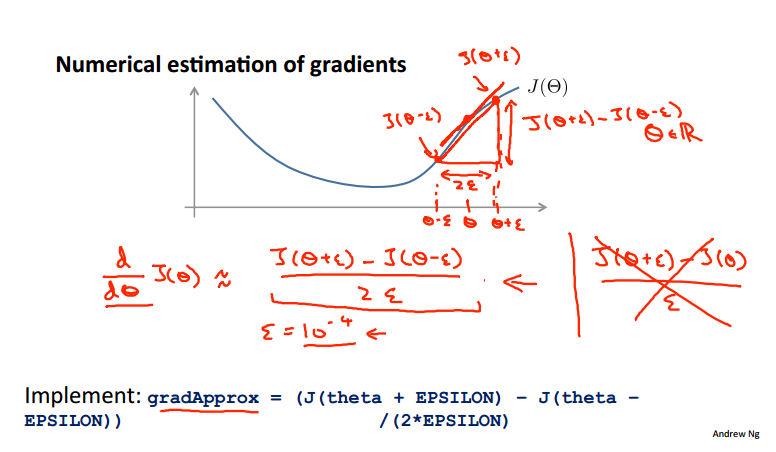
多个θ：

octave代码：

epsilon = 1e-4;
for i = 1:n,
  thetaPlus = theta;
  thetaPlus(i) += epsilon;
  thetaMinus = theta;
  thetaMinus(i) -= epsilon;
  gradApprox(i) = (J(thetaPlus) - J(thetaMinus))/(2*epsilon)
end;

 

步骤：

1. 使用反向传播计算D梯度值

2. 使用数值化方法计算gradApprX近似值

3. 确保他们的值很相似

4. 在接下来的过程中一定要把数值化计算法关闭

 

 

 

 

random initialization 随机初始化

我们在使用先进优化算法fminunc时，需要设置初始化的θ，如果我们全部设置为0则会有什么样的弊端呢？

 

 

激励值和误差首先会相等，梯度的计算以及更新后的参数都是相同的：

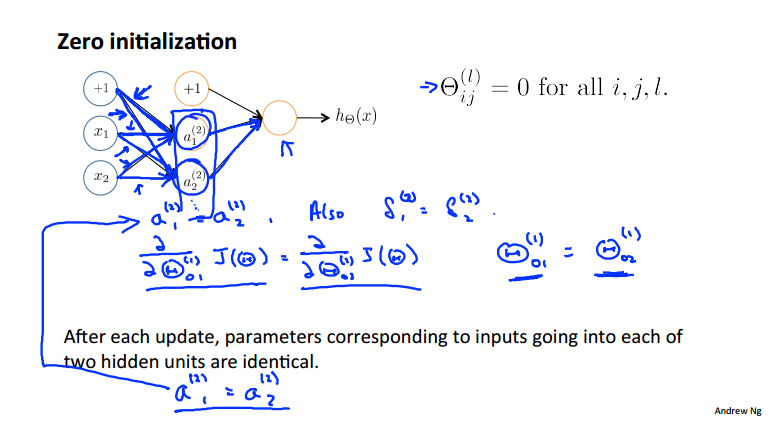
 所以我们引入了随机初始化的方法，用以打破对称结构，把每个参数θ映射到[-epsilon , epsilon]之间（为什么？）

If the dimensions of Theta1 is 10x11, Theta2 is 10x11 and Theta3 is 1x11.

Theta1 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta2 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta3 = rand(1,11) * (2 * INIT_EPSILON) - INIT_EPSILON;

 

总结 神经网络的有机结合

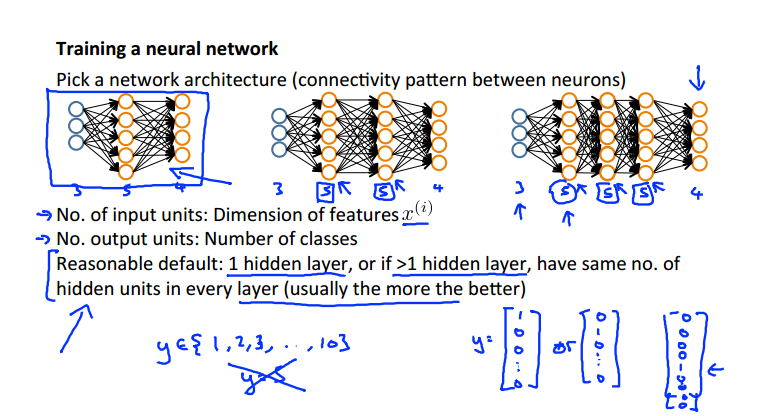
第一步：选择一个合适的网络结构

输入层单元个数：特征变量的维度

输出层单元个数：多分类的类别数目，注意要写成one hot representation的形式而不能是个具体的数值

隐藏层的规则：

1. 一般仅有一个隐藏层，如图一

2. 多个隐藏层的情况下，隐藏层的单元个数每层均相同，并且隐藏层单元越多越好

 

 第二步：训练神经网络六步

1. 随机初始化theta权重

2. 实现前向传播算法，得到每个输入样本对应的h预测输出值

3. 写cost function的代码

4. 实现反向传播算法计算cost function关于每个参数的偏导数

for i = 1:m,
   Perform forward propagation and backpropagation using example (x(i),y(i))
   (Get activations a(l) and delta terms d(l) for l = 2,...,L

 

5. 使用梯度检验比较反向传播得到的偏导和数值估算出的cost function的梯度值

6. 使用梯度下降或者高级算法来最小化cost function得到最终的θ值，便可以进行其他的预测

 

 h越接近y值的点，cost越低

 

 神经网络的应用 自动驾驶