knapsack背包问题python实现

1，问题描述
不同重量的物品对应的价值不同，对一个容量固定的背包来说，如何用背包装这些物品使得背包所装物品的总价值最高。

2，参数定义
背包的容量为：C（capacity）；
物品编号i对应的重量是：weight[i]；
物品编号i对应的价值是：value[i]。

3，解题思路
3.1,
我们最终要求的是背包所装物品的最高价值，则设最高价值为F；其总价值F是由包的容量（C）和所装的i个物品共同决定的，因此我们设价值F与背包容量C、i个物品的大小共同决定的，则设其函数对应关系为F(i,C)，其意义为使用i个物件充分填充空间C得到
的最大价值。

3.2,
若我们现在已知前i-1个物品填充容量为C的背包得到的最大价值是F(i-1,C)，现在考虑再放一个物品i到背包中，会出现以下2种情况：
1)，剩余容量太小，放不下物品i；
    如果放不下物品i，则表示前i个物品填充背包与前i-1个物品填充背包所得到的最高价值是一样的，即：
    F(i,C) = F(i-1,C)
2)，剩余容量足够，可以放下物品i。
    如果能放下物品i，则表示前i个物品填充背包与前i-1个物品填充背包所得到的最高值是不一样的，一定有个剩余容量能装下物品i的重量weight[i]，即前i-1个物品填充容量C-weight[i]，第i个物品填充剩余容量weight[i]，即前i个物品填充背
    包容量为C得到的总价值为前i-1个物品填充容量为C-weight[i]的背包，加上第i个物品填充剩余容量weight[i]，
    F(i,C) = F(i-1,C-weight[i]) + value[i]
对于上述两种情况而言，不论放第i个物品还是不放，只用取其总价值的最大值即可，即：
    F(i,C) = max(F(i-1,C), F(i-1,C-weight[i]) + value[i]) --式1

3.3,
得到上述函数表达式后，接下来需要确定边界值，背包容量C或前i个物品这2个变量中有一个为0则其总价值均为0，即：
    F(0,C) = 0;
    F(i,0) = 0;
    F(0,0) = 0.
    即：
    F(i,C) = 0  if i == 0 or C == 0 --式2

3.4,最后根据式1和式2得到：
F(i,C) = {
1），0    (while i == 0）
2），0    (while C == 0)
3），max(F(i-1,C), F(i-1,C-weight[i]) + value[i]) (while 当前的容量C >= 第i个物品的重量weight[i])
}

4，注意点：
1，弄清函数概念。
2，边界值确定。

---

5，示例代码

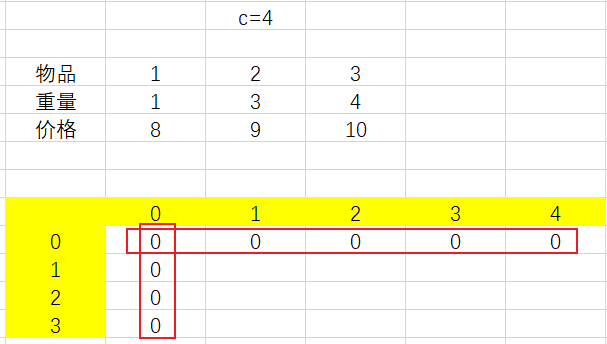
写代码的过程中可以在Excel写个例子，对照着写

def knapsack(weight, value, capacity):
    if len(weight) == 0 or len(value) == 0 or capacity == 0:
        return -1
    else:
        totalValue = [[0 for i in range(capacity + 1)] for j in range(len(value) + 1)]
        for ithGood in range(1, len(value) + 1):  # 1--4
            for currentCapacity in range(1, capacity + 1):  # 1--5
                if currentCapacity >= weight[ithGood-1]:
                    totalValue[ithGood][currentCapacity] = max(totalValue[ithGood - 1][currentCapacity],
                                                     totalValue[ithGood - 1][currentCapacity - weight[ithGood-1]]
                                                     + value[ithGood-1])
                else:
                    totalValue[ithGood][currentCapacity] = totalValue[ithGood - 1][currentCapacity]
        return totalValue[-1][-1]


if __name__ == '__main__':
    weightTest = [4, 5, 2, 1, 6]  # [2, 2, 6, 5, 4]
    valueTest = [4500, 5700, 2250, 1100, 6700]  # [6, 3, 5, 4, 6]
    capacityTest = 8  # 10
    print(knapsack(weightTest, valueTest, capacityTest))

6，参考文献

https://www.cnblogs.com/coded-ream/p/7208019.html

https://www.cnblogs.com/bugxch/p/13830904.html