deep learning with python前五章笔记

0. 基础

0. 基础

  • val_acc : Validation acc
  • acc : Training acc
  • batch
    • 深度学习的优化算法, 说白了就是梯度下降. 每次的参数更新有两种方式.
      • 第一种, 遍历全部数据集算一次损失函数, 然后算函数对各个参数的梯度, 更新梯度. 这种方法每更新一次参数都要把数据集里的所有样本都看一遍, 计算量开销大, 计算速度慢, 不支持在线学习, 这称为Batch gradient descent, 批梯度下降.
      • 另一种, 每看一个数据就算一下损失函数, 然后求梯度更新参数, 这个称为随机梯度下降, stochastic gradient descent. 这个方法速度比较快, 但是收敛性能不太好, 可能在最优点附近晃来晃去, hit不到最优点. 两次参数的更新也有可能互相抵消掉, 造成目标函数震荡的比较剧烈.
    • 为了克服两种方法的缺点, 现在一般采用的是一种折中手段, mini-batch gradient decent, 小批的梯度下降, 这种方法把数据分为若干个批, 按批来更新参数, 这样, 一个批中的一组数据共同决定了本次梯度的方向, 下降起来就不容易跑偏, 减少了随机性. 另一方面因为批的样本数与整个数据集相比小了很多, 计算量也不是很大.
    • 基本上现在的梯度下降都是基于mini-batch的, 所以Keras的模块中经常会出现batch_size, 就是指这个.
    • Keras中用的优化器SGD是stochastic gradient descent的缩写, 但不代表是一个样本就更新一回, 还是基于mini-batch的.
  • epochs
    • 指的就是训练过程中一批数据将被“轮”多少次
  • 影响精度的是损失值的分布，而不是平均值，因为精度是模型预测的类别概率的二进制阈值。即使从平均损失中无法看出，但模型也仍然可能在改进
    • 损失值的分布
      • 看他分布在阈值的哪一边
    • 二进制阈值
      • \(dst(z) = \begin{cases} maxVal\quad src(z) \gt threshold(阈值) \\ 0 \qquad\qquad otherwise\end{cases}\)
  • 验证集的目的就是验证不同的算法
1. 笔记

1. 笔记

  • 核函数是一个在计算上能够实现的操作, 将原始空间中的任意两点映射为这两点在目标表示空间中的距离, 完全避免了对新表示进行直接计算.
2. 笔记

2. 笔记

  • 小结
    • 学习是指找到一组模型参数, 使得在给定的训练数据样本和对应目标值上的损失函数最
      小化.
    • 学习的过程是指随机选取包含数据样本及其目标值的批量, 并计算批量损失相对于网络参数的梯度. 随后将网络参数沿着梯度的反方向稍稍移动(移动距离由学习率指定).
    • 整个学习过程之所以能够实现, 是因为神经网络是一系列可微分的张量运算, 因此可以
      利用求导的链式法则来得到梯度函数, 这个函数将当前参数和当前数据批量映射为一个梯度值.
    • 后续几章你会经常遇到两个关键的概念: 损失和优化器. 将数据输入网络之前, 你需要
      先定义这二者.
    • 损失是在训练过程中需要最小化的量, 因此, 它应该能够衡量当前任务是否已成功解决.
    • 优化器是使用损失梯度更新参数的具体方式, 比如RMSProp 优化器, 带动量的随机梯度下降(SGD)等.
  • 标量, 0D张量
    • 仅包含一个数字的张量
    • 标量张量有0 个轴
  • 向量(vector), 一维张量(1D 张量)
    • 数字组成的数组
    • 一维张量只有一个轴
  • 矩阵, 2D张量
    • 向量组成的数组
    • 矩阵有2个轴
  • 3D张量与更高维张量
    • 将多个矩阵组合成一个新的数组, 可以得到一个3D张量
  • 轴的个数, 阶(rank)
  • 形状
    • 标量的形状为空, 即()
    • 向量的形状只包含一个元素, 即(x, )
    • 矩阵的形状为(x, y)
    • 3D张量的形状为(x, y, z)
  • 通常来说, 深度学习中所有数据张量的第一个轴(0轴, 因为索引从0 开始)都是样本轴(samples axis, 有时也叫样本维度)
  • 深度学习模型会将数据拆分成小批量进行处理
    • 下面是是MNIST 数据集的一个批量, 批量大小为128.
    • 第一个批量
      • batch = train_images[:128]
    • 然后是下一个批量
      • batch = train_images[128:256]
    • 然后是第n 个批量
      • batch = train_images[128 * n:128 * (n + 1)]
    • 对于这种批量张量, 第一个轴(0 轴)叫作批量轴(batch axis)或批量维度(batch dimension)
  • 现实世界中的数据张量
    • 向量数据: 2D 张量, 形状为(samples, features).
    • 时间序列数据或序列数据: 3D 张量, 形状为(samples, timesteps, features).
    • 图像: 4D 张量, 形状为(samples, height, width, channels) 或(samples, channels, height, width).
    • 视频: 5D 张量, 形状为(samples, frames, height, width, channels) 或(samples, frames, channels, height, width).
  • 机器学习过程
    • 一开始, 这些权重矩阵取较小的随机值, 这一步叫作随机初始化(random initialization). 当然, W 和b 都是随机的, relu(dot(W, input) + b) 肯定不会得到任何有用的表示. 虽然得到的表示是没有意义的, 但这是一个起点. 下一步则是根据反馈信号逐渐调节这些权重. 这个逐渐调节的过程叫作训练, 也就是机器学习中的学习.
  • 反向传播
    • 利用网络中所有运算都是可微(differentiable)的这一事实, 计算损失相对于网络系数的梯度(gradient), 然后向梯度的反方向改变系数, 从而使损失降低.
  • 小批量随机梯度下降(mini-batch stochastic gradient descent, 又称为小批量SGD)
    • 沿着梯度的反方向更新权重, 损失每次都会变小一点.
    1. 抽取训练样本x 和对应目标y 组成的数据批量.
    2. 在x 上运行网络, 得到预测值y_pred.
    3. 计算网络在这批数据上的损失, 用于衡量y_pred 和y 之间的距离.
    4. 计算损失相对于网络参数的梯度［一次反向传播(backward pass)］.
    5. 将参数沿着梯度的反方向移动一点, 比如W -= step * gradient, 从而使这批数据上的损失减小一点.
  • 优化方法(optimization method)或优化器(optimizer)
    • SGD 的多种变体, 其区别在于计算下一次权重更新时还要考虑上一次权重更新, 而不是仅仅考虑当前梯度值, 比如带动量的SGD, Adagrad, RMSProp 等变体
  • 使用动量方法可以避免无法找到全局最小点
    • 就是将优化过程想象成一个小球从损失函数曲线上滚下来. 如果小球的动量足够大, 那么它不会卡在峡谷里, 最终会到达全局最小点
    • 动量方法的实现过程是每一步都移动小球, 不仅要考虑当前的斜率值(当前的加速度), 还要考虑当前的速度(来自于之前的加速度).
    • 这在实践中的是指, 更新参数w 不仅要考虑当前的梯度值, 还要考虑上一次的参数更新
    • 其简单实现如下所示
      past_velocity = 0.
momentum = 0.1      #不变的动量因子
while loss > 0.01:  #优化循环
    w, loss, gradient = get_current_parameters()
    velocity = past_velocity * momentum - learning_rate * gradient
    w = w + momentum * velocity - learning_rate * gradient
    past_velocity = velocity
    update_parameter(w)
  • 网络的编译
    network.compile(
    optimizer='rmsprop',
    loss='categorical_crossentropy',
    metrics=['accuracy']
    )
    • categorical_crossentropy 是损失函数, 是用于学习权重张量的反馈信号, 在训练阶段应使它最小化.
    • 减小损失是通过小批量随机梯度下降来实现的. 梯度下降的具体方法由第一个参数给定, 即rmsprop 优化器
  • 训练循环
    network.fit(
    train_images, 
    train_labels, 
    epochs=5, 
    batch_size=128
    )
    • 网络开始在训练数据上进行迭代(每个小批量包含128 个样本), 共迭代5 次［在所有训练数据上迭代一次叫作一个轮次(epoch)］
    • 在每次迭代过程中, 网络会计算批量损失相对于权重的梯度, 并相应地更新权重.
    • 5 轮之后, 网络进行了2345 次梯度更新(60000个样本, 60000/128 = 468.75. 也就是每轮469 次), 网络损失值将变得足够小, 使得网络能够以很高的精度对手写数字进行分类.
3. 笔记

3. 笔记

  • 小结
    • 通常需要对原始数据进行大量预处理, 以便将其转换为张量输入到神经网络中. 单词序列可以编码为二进制向量, 但也有其他编码方式.
    • 带有relu激活的Dense层堆叠, 可以解决很多种问题(包括情感分类), 你可能会经常用到这种模型.
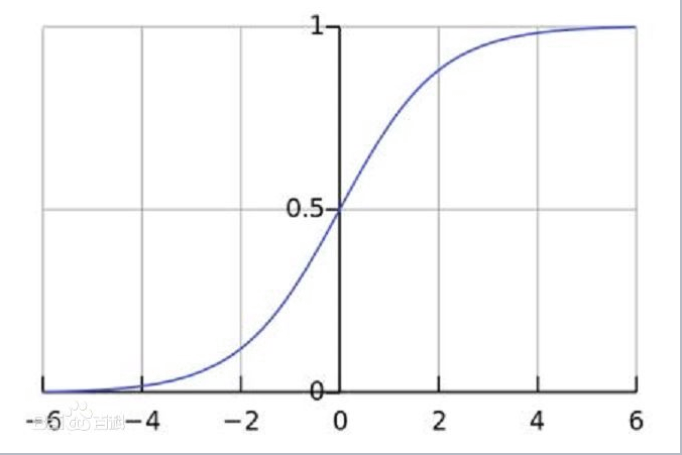
    • 对于二分类问题(两个输出类别), 网络的最后一层应该是只有一个单元并使用sigmoid激活的Dense层, 网络输出应该是0~1范围内的标量, 表示概率值.
    • 对于二分类问题的sigmoid标量输出, 你应该使用binary_crossentropy损失函数.
    • 无论你的问题是什么, rmsprop优化器通常都是足够好的选择. 这一点你无须担心.
    • 随着神经网络在训练数据上的表现越来越好, 模型最终会过拟合, 并在前所未见的数据上得到越来越差的结果. 一定要一直监控模型在训练集之外的数据上的性能.
    • 如果要对N个类别的数据点进行分类, 网络的最后一层应该是大小为N的Dense层.
    • 对于单标签, 多分类问题, 网络的最后一层应该使用softmax激活, 这样可以输出在N个输出类别上的概率分布.
    • 这种问题的损失函数几乎总是应该使用分类交叉熵. 它将网络输出的概率分布与目标的真实分布之间的距离最小化.
    • 处理多分类问题的标签有两种方法.
      • 通过分类编码(也叫one-hot编码)对标签进行编码, 然后使用categorical_crossentropy作为损失函数.
      • 将标签编码为整数, 然后使用sparse_categorical_crossentropy损失函数.
    • 如果你需要将数据划分到许多类别中, 应该避免使用太小的中间层, 以免在网络中造成信息瓶颈.
    • 回归问题使用的损失函数与分类问题不同. 回归常用的损失函数是均方误差(MSE).
    • 同样, 回归问题使用的评估指标也与分类问题不同. 显而易见, 精度的概念不适用于回归问题. 常见的回归指标是平均绝对误差(MAE).
    • 如果输入数据的特征具有不同的取值范围, 应该先进行预处理, 对每个特征单独进行缩放.
    • 如果可用的数据很少, 使用K 折验证可以可靠地评估模型.
    • 如果可用的训练数据很少, 最好使用隐藏层较少(通常只有一到两个)的小型网络, 以避免严重的过拟合.
  • 训练神经网络主要围绕以下四个方面
    • 层, 多个层组合成网络(或模型).
    • 输入数据和相应的目标.
    • 损失函数, 即用于学习的反馈信号.
    • 优化器, 决定学习过程如何进行.
  • 不同的张量格式与不同的数据处理类型需要用到不同的层
    • 简单的向量数据保存在形状为(samples, features) 的2D 张量中, 通常用密集连接层［densely connected layer, 也叫全连接层(fully connected layer)或密集层(dense layer), 对应于Keras 的Dense 类］来处理.
    • 序列数据保存在形状为(samples, timesteps, features) 的3D 张量中, 通常用循环层(recurrent layer, 比如Keras 的LSTM 层)来处理.
    • 图像数据保存在4D 张量中, 通常用二维卷积层(Keras 的Conv2D)来处理.
  • 损失函数(目标函数)
    • 在训练过程中需要将其最小化. 它能够衡量当前任务是否已成功完成.
  • 优化器
    • 决定如何基于损失函数对网络进行更新. 它执行的是随机梯度下降(SGD)的某个变体.
  • 将整数序列编码为二进制矩阵, one-host编码
    import numpy as np
#转换为10 000 维向量当索引(是向量不是张量), 对应10 000个最常见的单词
def vectorize_sequences(sequences, dimension=10000):
    #创建一个形状为(len(sequences),dimension) 的零矩阵
    results = np.zeros((len(sequences), dimension))
    for i, sequence in enumerate(sequences):
        results[i, sequence] = 1.           #将results[i] 的指定索引设为1
    return results
x_train = vectorize_sequences(train_data)   #将训练数据向量化
x_test = vectorize_sequences(test_data)     #将测试数据向量化
  • 如果面对一个二分类问题, 网络输出是一个概率值(网络最后一层使用sigmoid 激活函数, 仅包含一个单元), 那么最好使用binary_crossentropy(二元交叉熵)损失. 这并不是唯一可行的选择, 比如你还可以使用mean_squared_error(均方误差). 但对于输出概率值的模型, 交叉熵(crossentropy)往往是最好的选择.
    • 交叉熵是来自于信息论领域的概念, 用于衡量概率分布之间的距离, 在这个例子中就是真实分布与预测值之间的距离.
  • history = model.fit()
    • history.history, 它是一个字典, 包含训练过程中的所有数据.
  • 单标签, 多分类(single-label, multiclass classification)问题
    • 每个数据点只能划分到一个类别(主题)
  • 多标签, 多分类(multilabel,multiclass classification)问题
    • 每个数据点可以划分到多个类别(主题)
  • keras.utils.to_categorical函数是把类别标签转换为onehot编码
  • logistic 回归不是回归算法, 而是分类算法.
  • 取值范围差异很大的数据普遍采用的最佳实践是对每个特征做标准化, 即对于输入数据的每个特征(输入数据矩阵中的列), 减去特征平均值, 再除以标准差, 这样得到的特征平均值为0, 标准差为1
    • x = (x - mean)/std
  • mse 损失函数 均方误差(MSE, mean squared error),
    • 预测值与目标值之差的平方
    • 回归问题常用的损失函数
  • 平均绝对误差(MAE, mean absolute error). 它是预测值与目标值之差的绝对值.
    • 在训练过程中监控的一个指标
  • EMA 指数移动平均值
    • EMA = aNow + (1-a)Pre_EMA
    • 更能反映近期价格的变化趋势. 可以减少极端值的影响, 可平滑数据序列, 这使变动数据更易于分析.
4. 笔记

4. 笔记

  • 小结

    • 定义问题与要训练的数据. 收集这些数据, 有需要的话用标签来标注数据.
    • 选择衡量问题成功的指标. 你要在验证数据上监控哪些指标？
    • 确定评估方法：留出验证？K 折验证？你应该将哪一部分数据用于验证？
    • 开发第一个比基准更好的模型, 即一个具有统计功效的模型.
    • 开发过拟合的模型.
    • 基于模型在验证数据上的性能来进行模型正则化与调节超参数. 许多机器学习研究往往只关注这一步, 但你一定要牢记整个工作流程.

  • 深度学习的概念框架

    1. 模型评估
    2. 数据预处理
    3. 特征工程
    4. 解决过拟合

  • 无监督学习

    • 在没有目标的情况下寻找输入数据的有趣变换
    • 目的: 数据可视化, 数据压缩, 数据去噪或更好地理解数据中的相关性

  • 自监督学习

    • 可以将它看作没有人类参与的监督学习
    • 标签仍然存在(因为总要有什么东西来监督学习过程), 但它们是从输入数据中生成的, 通常是使用启发式算法生成的

  • 分类和回归术语表

    • 样本(sample)或输入(input)
      • 进入模型的数据点.
    • 预测(prediction)或输出(output)
      • 从模型出来的结果.
    • 目标(target)
      • 真实值. 对于外部数据源, 理想情况下, 模型应该能够预测出目标.
    • 预测误差(prediction error)或损失值(loss value)
      • 模型预测与目标之间的距离.
    • 类别(class)
      • 分类问题中供选择的一组标签. 例如, 对猫狗图像进行分类时, "狗"和"猫"就是两个类别.
    • 标签(label)
      • 分类问题中类别标注的具体例子. 比如, 如果1234 号图像被标注为包含类别"狗", 那么"狗"就是1234 号图像的标签.
    • 真值(ground-truth)或标注(annotation)
      • 数据集的所有目标, 通常由人工收集.
    • 二分类(binary classification)
      • 一种分类任务, 每个输入样本都应被划分到两个互斥的类别中.
    • 多分类(multiclass classification)
      • 一种分类任务, 每个输入样本都应被划分到两个以上的类别中, 比如手写数字分类.
    • 多标签分类(multilabel classification)
      • 一种分类任务, 每个输入样本都可以分配多个标签. 举个例子, 如果一幅图像里可能既有猫又有狗, 那么应该同时标注"猫"标签和"狗"标签. 每幅图像的标签个数通常是可变的.
    • 标量回归(scalar regression)
      • 目标是连续标量值的任务. 预测房价就是一个很好的例子, 不同的目标价格形成一个连续的空间.
    • 向量回归(vector regression)
      • 目标是一组连续值(比如一个连续向量)的任务. 如果对多个值(比如图像边界框的坐标)进行回归, 那就是向量回归.
    • 小批量(mini-batch)或批量(batch)
      • 模型同时处理的一小部分样本(样本数通常为8~128). 样本数通常取2 的幂, 这样便于GPU 上的内存分配. 训练时, 小批量用来为模型权重计算一次梯度下降更新.

  • 留出验证

    num_validation_samples = 10000
np.random.shuffle(data) #通常需要打乱数据
validation_data = data[:num_validation_samples]
data = data[num_validation_samples:]
training_data = data[:]
model = get_model()
model.train(training_data)
validation_score = model.evaluate(validation_data)
# 现在你可以调节模型, 重新训练, 评估, 然后再次调节……
#一旦调节好超参数, 通常就在所有非测试数据上从头开始训练最终模型
model = get_model()
model.train(np.concatenate([training_data,validation_data]))
test_score = model.evaluate(test_data)

  • 带有打乱数据的重复K 折验证

    • 具体做法是多次使用K 折验证, 在每次将数据划分为K 个分区之前都先将数据打乱. 最终分数是每次K 折验证分数的平均值. 注意, 这种方法一共要训练和评估P×K 个模型(P是重复次数), 计算代价很大

  • 数据代表性(data representativeness)

    • 在将数据划分为训练集和测试集之前, 通常应该随机打乱数据

  • 时间箭头(the arrow of time)

    • 如果想要根据过去预测未来(比如明天的天气, 股票走势等), 那么在划分数据前你不应该随机打乱数据, 因为这么做会造成时间泄露(temporalleak)：你的模型将在未来数据上得到有效训练.
    • 在这种情况下, 你应该始终确保测试集中所有数据的时间都晚于训练集数据

  • 数据冗余(redundancy in your data)

    • 一定要确保训练集和验证集之间没有交集

  • 神经网络的数据预处理

    1. 数据向量化(data vectorization)
      • 神经网络的所有输入和目标都必须是浮点数张量(在特定情况下可以是整数张量,无论处理什么数据(声音、图像还是文本))
    2. 值标准化
      • 输入数据应该具有以下特征
        • 取值较小：大部分值都应该在0~1 范围内.
        • 同质性(homogenous)：所有特征的取值都应该在大致相同的范围内.
      • 更严格的标准化方法
        • 将每个特征分别标准化, 使其平均值为0.
        • 将每个特征分别标准化, 使其标准差为1.
          • 标准差\(\sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N}{(x_i-\mu)^2}}\)
        #假设x 是一个形状为(samples,features) 的二维矩阵
x -= x.mean(axis=0)
x /= x.std(axis=0)
    3. 处理缺失值
      • 一般来说, 对于神经网络网络能够从数据中学到0 意味着缺失数据, 并且会忽略这个值.
      • 如果测试数据中可能有缺失值, 而网络是在没有缺失值的数据上训练的, 在这种情况下, 你应该人为生成一些有缺失项的训练样本：多次复制一些训练样本, 然后删除测试数据中可能缺失的某些特征.

  • 特征工程(feature engineering)

    • 将数据输入模型之前, 利用你自己关于数据和机器学习算法(这里指神经网络)的知识对数据进行硬编码的变换(不是模型学到的), 以改善模型的效果.
    • 特征工程的本质
      • 用更简单的方式表述问题, 从而使问题变得更容易. 它通常需要深入理解问题.
    • 良好的特征仍然可以让你用更少的资源更优雅地解决问题. 例如, 使用卷积神经网络来读取钟面上的时间是非常可笑的.
    • 良好的特征可以让你用更少的数据解决问题.

  • 过拟合与欠拟合

    • 机器学习的根本问题是优化和泛化之间的对立.
    • 优化(optimization)
      • 调节模型以在训练数据上得到最佳性能(即机器学习中的学习)
    • 泛化(generalization)
      • 训练好的模型在前所未见的数据上的性能好坏. 机器学习的目的当然是得到良好的泛化, 但你无法控制泛化, 只能基于训练数据调节模型.
    1. 训练开始时, 优化和泛化是相关的：
      • 训练数据上的损失越小, 测试数据上的损失也越小. 这时的模型是欠拟合(underfit)的, 即仍有改进的空间, 网络还没有对训练数据中所有相关模式建模.
    2. 在训练数据上迭代一定次数之后, 泛化不再提高, 验证指标先是不变, 然后开始变差, 即模型开始过拟合.
      • 正则化(regularization): 降低过拟合的方法
        • 最优解决方法是获取更多的训练数据.
          • 模型的训练数据越多, 泛化能力自然也越好.
        • 次优解决方法是调节模型允许存储的信息量, 或对模型允许存储的信息加以约束.
          • 如果一个网络只能记住几个模式, 那么优化过程会迫使模型集中学习最重要的模式, 这样更可能得到良好的泛化
        • 减小网络大小
          • 防止过拟合的最简单的方法,即减少模型中可学习参数的个数(这由层数和每层的单元个数决定)
        • 添加权重正则化(weight regularization)
          • 强制让模型权重只能取较小的值, 从而限制模型的复杂度, 使得权重值的分布更加规则(regular)
          • 实现方法是向网络损失函数中添加与较大权重值相关的成本(cost)
            • 范数:\(||x||_p = (\sum_{i=1}^n|x_i|^p)^{\frac{1}{p}}\)
              • p=1: L1范数
              • p=2: L2范数
            • 预测的函数: \(h_\theta(x)\)
            • 误差公式: \(J(\theta) = [h_\theta(x)-y_\theta]^2\)
            • L1正则化(L1 regularization)
              • 添加的成本与权重系数的绝对值［权重的L1 范数(norm)］成正比.
              • \(J(\theta) = \frac{1}{2m}[\sum_{i=1}^m(h_\theta(x_i)-y_i)^2+\lambda\sum_{j=1}^n|\theta_j|]\)
                • \(\lambda\) 是l1的参数
                • n 是隐藏单元数量
                • m 是训练样本的个数
                • 2m 是为了方便计算梯度下降
            • L2正则化(或权重衰减) (L2 regularization)(weight decay)
              • 添加的成本与权重系数的平方(权重的L2 范数)成正比
              • \(J(\theta) = \frac{1}{2m}[\sum_{i=1}^m(h_\theta(x_i)-y_i)^2+\lambda\sum_{j=1}^n\theta_j^2]\)
                • \(\lambda\) 是l2的参数
                • n 是隐藏单元数量
                • m 是训练样本的个数
                • 2m 是为了方便计算梯度下降
          • 在Keras 中, 添加权重正则化的方法是向层传递权重正则化项实例(weight regularizerinstance)作为关键字参数.
            from keras import regularizers
model = models.Sequential()
model.add(
    layers.Dense(
        16,
        #L1 正则化
        #kernel_regularizer=regularizers.l1(0.001),
        #L2 正则化
        kernel_regularizer=regularizers.l2(0.001),
        #同时L1 L2正则化
        #kernel_regularizer=regularizers.l1_l2(l1=0.001,l2=0.001),
    )
)
        • 添加dropout 正则化
          • dropout 是神经网络最有效也最常用的正则化方法之一
          • 对某一层使用dropout, 就是在训练过程中随机将该层的一些输出特征舍弃(设置为0)
          • dropout 比率(dropout rate)是被设为0 的特征所占的比例, 通常在0.2~0.5范围内
          • 例
            • 训练时, 随机将矩阵中一部分值设为0
              #dropout, 一个仅包含随机0或1的矩阵(0的概率是0.5, 1的概率是0.5),且与layer_out的形状相同
dropout = np.random.randint(0, high=2, size=layer_output.shape)
#舍弃50%的输出单元
layer_output *= dropout
            • 测试时, 我们将输出按dropout比率缩小. 这里我们乘以0.5(因为前面舍弃了一半的单元)
              • 因为测试时比训练时有更多的单元被激活, 需要加以平衡
              layer_output *= 0.5
            • 还可以让两个运算都在训练时进行, 而测试时输出保持不变. 这通常也是实践中的实现方式
              layer_output *= np.random.randint(0, high=2, size=layer_output.shape)#训练时
layer_output /= 0.5     #成比例放大
          • 其核心思想是在层的输出值中引入噪声, 打破不显著的偶然模式(Hinton 称之为阴谋). 如果没有噪声的话, 网络将会记住这些偶然模式.
        • 防止神经网络过拟合的常用方法包括
          • 获取更多的训练数据
          • 减小网络容量
          • 添加权重正则化
          • 添加dropout
    • 深度学习模型通常都很擅长拟合训练数据, 但真正的挑战在于泛化
    • 模型应在容量过大与容量不足之间要找到一个折中
      • 容量: 模型中可学习参数的个数
    • 一般的工作流程是开始时选择相对较少的层和参数, 然后逐渐增加层的大小或增加新层, 直到这种增加对验证损失的影响变得很小.

  • 非平稳问题(nonstationary problem)

    • 假设你想要构建一个服装推荐引擎, 并在一个月(八月)的数据上训练, 然后在冬天开始生成推荐结果. 一个大问题是, 人们购买服装的种类是随着季节变化的, 即服装购买在几个月的尺度上是一个非平稳现象.
    • 请记住, 机器学习只能用来记忆训练数据中存在的模式. 你只能识别出曾经见过的东西. 在过去的数据上训练机器学习来预测未来, 这里存在一个假设, 就是未来的规律与过去相同. 但事实往往并非如此.
    • 对于平衡分类问题(每个类别的可能性相同)
      • 精度和接收者操作特征曲线下面积(areaunder the receiver operating characteristic curve, ROC AUC)是常用的指标.
    • 对于类别不平衡的问题
      • 你可以使用准确率和召回率. 对于排序问题或多标签分类, 你可以使用平均准确率均值(mean average precision). 自定义衡量成功的指标也很常见.

  • 确定评估方法

    • 留出验证集. 数据量很大时可以采用这种方法.
    • K 折交叉验证. 如果留出验证的样本量太少, 无法保证可靠性, 那么应该选择这种方法.
    • 重复的K 折验证. 如果可用的数据很少, 同时模型评估又需要非常准确, 那么应该使用这种方法.
    • 只需选择三者之一. 大多数情况下, 第一种方法足以满足要求.

  • 准备数据

    • 应将数据格式化为张量.
    • 这些张量的取值通常应该缩放为较小的值, 比如在[-1, 1] 区间或[0, 1] 区间.
    • 如果不同的特征具有不同的取值范围(异质数据), 那么应该做数据标准化.
    • 你可能需要做特征工程, 尤其是对于小数据问题.

  • 开发比基准更好的模型

    • 目标是获得统计功效(statistical power), 即开发一个小型模型, 它能够打败纯随机的基准(dumb baseline).
    • 任何精度大于\(\frac{1}{标签个数}\)的模型都可以说具有统计功效
      • 精度: 预测值与真值的接近程度

  • 选择三个关键参数来构建第一个工作模型

    • 最后一层的激活. 它对网络输出进行有效的限制. 例如, IMDB 分类的例子在最后一层使用了sigmoid, 回归的例子在最后一层没有使用激活, 等等.
    • 损失函数. 它应该匹配你要解决的问题的类型. 例如, IMDB 的例子使用binary_crossentropy、回归的例子使用mse, 等等.
      • 需要注意, 直接优化衡量问题成功的指标不一定总是可行的. 有时难以将指标转化为损失函数, 要知道, 损失函数需要在只有小批量数据时即可计算(理想情况下, 只有一个数据点时, 损失函数应该也是可计算的), 而且还必须是可微的(否则无法用反向传播来训练网络).
    • 优化配置. 你要使用哪种优化器？学习率是多少？大多数情况下, 使用rmsprop 及其默认的学习率是稳妥的.

  • 为模型选择正确的最后一层激活和损失函数

    问题类型 最后一层激活 损失函数
    二分类问题 sigmoid binary_crossentropy
    多分类、单标签问题 softmax categorical_crossentropy
    多分类、多标签问题 sigmoid binary_crossentropy
    回归到任意值 无 mse
    回归到0~1 范围内的值 sigmoid mse 或binary_crossentropy
    • softmax

  • 开发过拟合的模型

    • 理想的模型是刚好在欠拟合和过拟合的界线上, 在容量不足和容量过大的界线上. 为了找到这条界线, 你必须穿过它. 要搞清楚你需要多大的模型, 就必须开发一个过拟合的模型
    1. 添加更多的层.
    2. 让每一层变得更大.
    3. 训练更多的轮次.
    • 要始终监控训练损失和验证损失, 以及你所关心的指标的训练值和验证值. 如果你发现模型在验证数据上的性能开始下降, 那么就出现了过拟合.
    • 下一阶段将开始正则化和调节模型, 以便尽可能地接近理想模型, 既不过拟合也不欠拟合.

  • 模型正则化与调节超参数

    1. 添加dropout.
    2. 尝试不同的架构：增加或减少层数.
    3. 添加L1 (和/或) L2 正则化.
    4. 尝试不同的超参数(比如每层的单元个数或优化器的学习率), 以找到最佳配置.
    5. (可选)反复做特征工程：添加新特征或删除没有信息量的特征.
    • 每次使用验证过程的反馈来调节模型, 都会将有关验证过程的信息泄露到模型中. 但如果系统性地迭代许多次, 最终会导致模型对验证过程过拟合(即使模型并没有直接在验证数据上训练). 这会降低验证过程的可靠性.
    • 一旦开发出令人满意的模型配置, 你就可以在所有可用数据(训练数据+ 验证数据)上训练最终的生产模型, 然后在测试集上最后评估一次. 如果测试集上的性能比验证集上差很多, 那么这可能意味着你的验证流程不可靠, 或者你在调节模型参数时在验证数据上出现了过拟合. 在这种情况下, 你可能需要换用更加可靠的评估方法, 比如重复的K 折验证
5. 笔记

5. 笔记

  • 小结
    • 卷积神经网络是用于计算机视觉任务的最佳机器学习模型。即使在非常小的数据集上也可以从头开始训练一个卷积神经网络，而且得到的结果还不错。
    • 在小型数据集上的主要问题是过拟合。在处理图像数据时，数据增强是一种降低过拟合的强大方法。
    • 利用特征提取，可以很容易将现有的卷积神经网络复用于新的数据集。对于小型图像数据集，这是一种很有价值的方法。
    • 作为特征提取的补充，你还可以使用微调，将现有模型之前学到的一些数据表示应用于新问题。这种方法可以进一步提高模型性能。
    • 卷积神经网络通过学习模块化模式和概念的层次结构来表示视觉世界。
    • 卷积神经网络学到的表示很容易可视化，卷积神经网络不是黑盒。
    • 可以将卷积神经网络学到的过滤器可视化，也可以将类激活热力图可视化。
  • 例
    #卷积神经网络
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)))
model.add(layers.MaxPooling2D((2, 2)))
  • layers.Conv2D(filters, kernl_size, activation, input_shape)
    • filters：卷积核的数目(即输出的维度)
    • kernel_size：卷积核的空域或时域窗长度
    • input_shape :整数元组, 不包括样本数的轴
  • layers.MaxPooling2D(pool_size)
    • pool_size：长为2的整数tuple, 代表在两个方向(竖直, 水平)上的下采样因子
  • 宽度和高度两个维度的尺寸通常会随着网络加深而变小. 通道数量由传入Conv2D 层的第一个参数所控制(32 或64).
  • 密集连接层和卷积层的根本区别
    • Dense 层从输入特征空间中学到的是全局模式(比如对于MNIST 数字, 全局模式就是涉及所有像素的模式)
    • 卷积层学到的是局部模式, 对于图像来说, 学到的就是在输入图像的二维小窗口中发现的模式.
  • 卷积神经网络具有以下两个有趣的性质
    • 卷积神经网络学到的模式具有平移不变性(translation invariant). 卷积神经网络在图像右下角学到某个模式之后, 它可以在任何地方识别这个模式, 比如左上角
      • 因为视觉世界从根本上具有平移不变性
    • 卷积神经网络可以学到模式的空间层次结构(spatial hierarchies of patterns)
      • 因为视觉世界从根本上具有空间层次结构
  • 特征图(feature map)
    • 对于包含两个空间轴(高度和宽度)和一个深度轴(也叫通道轴)的3D 张量的卷积
  • 卷积运算从输入特征图中提取图块, 并对所有这些图块应用相同的变换, 生成输出特征图(outputfeature map). 该输出特征图仍是一个3D 张量, 具有宽度和高度, 其深度可以任意取值, 因为输出深度是层的参数, 深度轴的不同通道代表过滤器(filter). 过滤器对输入数据的某一方面进行编码,
  • 输出通道(output channel) = 过滤器(filter) = 特征(feture)
  • 卷积的工作原理
    • 在3D 输入特征图上滑动(slide)这些3×3 或5×5 的窗口, 在每个可能的位置停止并提取周围特征的3D 图块. 然后每个3D 图块与学到的同一个权重矩阵做张量积, 转换成形状为(output_depth,) 的1D 向量. 然后对所有这些向量进行空间重组, 使其转换为形状为(height, width, output_depth) 的3D 输出特征图. 输出特征图中的每个空间位置都对应于输入特征图中的相同位置(比如输出的右下角包含了输入右下角的信息)
      • 3D 图块: 形状为(window_height, window_width, input_depth)
      • 卷积核(convolution kernel): 每个3D 图块与学到的同一个权重矩阵
  • 填充(padding)
    • 填充是在输入特征图的每一边添加适当数目的行和列,
    • 如果你希望输出特征图的空间维度与输入相同, 那么可以使用
    • 对于Conv2D 层, 可以通过padding 参数来设置填充
      • padding 参数的默认值为valid
      • valid: 表示不使用填充
      • same: 表示填充后输出的宽度和高度与输入相同
  • 步进卷积
    • 步幅: 两个连续窗口的距离
    • 实践中很少使用
  • 最大池化运算
    • 在每个MaxPooling2D 层之后, 特征图的尺寸都会减半.
    • 作用: 对特征图进行下采样, 与步进卷积类似.
    • 与卷积的最大不同之处:
      • 最大池化通常使用2×2 的窗口和步幅2, 其目的是将特征图下采样2 倍.
      • 卷积通常使用3×3 窗口和步幅1.
    • 用这种方式对特征图下采样的原因
      • 减少需要处理的特征图的元素个数
      • 通过让连续卷积层的观察窗口越来越大(即窗口覆盖原始输入的比例越来越大), 从而引入空间过滤器的层级结构
  • 卷积神经网络学到的是局部的、平移不变的特征, 它对于感知问题可以高效地利用数据.
  • 构建网络
    • 当处理的是更大的图像和更复杂的问题, 你需要相应地增大网络, 即再增加一个Conv2D+MaxPooling2D 的组合. 这既可以增大网络容量, 也可以进一步减小特征图的尺寸, 使其在连接Flatten 层时尺寸不会太大.
  • keras.preprocessing.image.ImageDataGenerator 类
    • 可以快速创建Python 生成器, 能够将硬盘上的图像文件自动转换为预处理好的张量批量
    train_datagen = ImageDataGenerator(
    rescale=1./255
    )  #将所有图像乘以1/255 缩放
train_generator = train_datagen.flow_from_directory(
    train_dir,  #目标目录
    target_size=(150, 150), #将所有图像的大小调整为150×150
    batch_size=20,  #批量大小: 每个批量中包含20个样本
    class_mode='binary' #因为使用了binary_crossentropy损失, 所以需要用二进制标签
    )
history = model.fit_generator(
    train_generator,
    steps_per_epoch=100,
    epochs=30,
    validation_data=validation_generator,
    validation_steps=50
    """
    steps_per_epoch:
        从训练生成器中抽取数据批量的次数
        = 训练图像数量 / 一个批量包含样本数量

    epochs:
        一批数据被"轮"次数

    validation_steps:
        从验证生成器中抽取数据批量的次数
        = 验证图像数量 / 一个批量包含样本数量
    """
    )
model.save('cats_and_dogs_small_1.h5')
  • 数据增强
    • 数据增强是从现有的训练样本中生成更多的训练数据, 其方法是利用多种能够生成可信图像的随机变换来增加(augment)样本
    • 数据增强对防止小型图像数据集的过拟合非常重要。
    datagen = ImageDataGenerator(
    rotation_range=40,
    width_shift_range=0.2,
    height_shift_range=0.2,
    shear_range=0.2,
    zoom_range=0.2,
    horizontal_flip=True,
    fill_mode='nearest'
    )
history = model.fit_generator(
    train_generator,
    steps_per_epoch=100,
    epochs=100,
    validation_data=validation_generator,
    validation_steps=50
    )
    • rotation_range: 表示图像随机旋转的角度范围（在0~180 范围内）
    • width_shift 和height_shift: 图像在水平或垂直方向上平移的范围（相对于总宽度或总高度的比例）
    • shear_range 是随机错切变换的角度。
    • zoom_range 是图像随机缩放的范围。
    • horizontal_flip 是随机将一半图像水平翻转。如果没有水平不对称的假设（比如真实世界的图像），这种做法是有意义的。
    • fill_mode是用于填充新创建像素的方法，这些新像素可能来自于旋转或宽度/高度平移。
    • 注意，不能增强 验证数据(validate data)
  • 为了进一步降低过拟合，你还需要向模型中添加一个Dropout 层，添加到密集连接分类器之前
    #Conv2D and MaxPooling2D...
model.add(layers.Flatten())
model.add(layers.Dropout(0.5))
  • 使用预训练的卷积神经网络
    • 预训练网络（pretrained network）是一个保存好的网络，之前已在大型数据集（通常是大规模图像分类任务）上训练好
    • 这种学到的特征在不同问题之间的可移植性，它使得深度学习对小数据问题非常有效
    • 使用预训练网络有两种方法
      • 特征提取（feature extraction）
        • 特征提取是使用之前网络学到的表示来从新样本中提取出有趣的特征。然后将这些特征输入一个新的分类器，从头开始训练。
        • 一系列池化层和卷积层叫作模型的卷积基（convolutional base）
        • 对于卷积神经网络而言，特征提取就是取出之前训练好的网络的卷积基，在上面运行新数据，然后在输出上面训练一个新的分类器
        • 某个卷积层提取的表示的通用性（以及可复用性）取决于该层在模型中的深度。
          • 模型中更靠近底部的层提取的是局部的、高度通用的特征图（比如视觉边缘、颜色和纹理）
          • 而更靠近顶部的层提取的是更加抽象的概念（比如“猫耳朵”或“狗眼睛”）
          • 因此，如果你的新数据集与原始模型训练的数据集有很大差异，那么最好只使用模型的前几层来做特征提取，而不是使用整个卷积基
        • 将VGG16 卷积基实例化
          from keras.applications import VGG16
conv_base = VGG16(
    weights='imagenet',
    include_top=False,
    input_shape=(150, 150, 3)
    )
          • include_top：是否保留顶层的3个全连接网络
          • weights：
            • None代表随机初始化，即不加载预训练权重
            • imagenet代表加载预训练权重
            • input_shape是输入到网络中的图像张量的形状。这个参数完全是可选的，如果不传入这个参数，那么网络能够处理任意形状的输入。
        • 在特征上添加一个密集连接分类器的两张办法
          1. 在你的数据集上运行卷积基，将输出保存成硬盘中的Numpy 数组，然后用这个数据作为输入，输入到独立的密集连接分类器中
            • 这种方法速度快，计算代价低,但这种方法不允许你使用数据增强
          2. 在顶部添加Dense 层来扩展已有模型（即conv_base），并在输入数据上端到端地运行整个模型。
            • 可以使用数据增强，但这种方法的计算代价比第一种要高很多
            • 冻结卷积层: 就是卷积层已经训练好了, 不再让他训练了
              • conv_base.trainable = False
              • 在model.compile前写
      • 微调模型（fine-tuning）
        • 对于用于特征提取的冻结的模型基，微调是指将其顶部的几层“解冻”，并将这解冻的几层和新增加的部分联合训练。它只是略微调整了所复用模型中更加抽象的表示
        • 微调网络的步骤如下
          1. 在已经训练好的基网络（base network）上添加自定义网络
          2. 冻结基网络
          3. 训练所添加的部分
          4. 解冻基网络的一些层
          5. 联合训练解冻的这些层和添加的部分
        • 我们将使用学习率非常小的RMSProp 优化器来实现。之所以让学习率很小，是因为对于微调的三层表示，我们希望其变化范围不要太大。太大的权重更新可能会破坏这些表示
  • 卷积神经网络的可视化
    • 可视化卷积神经网络的过滤器：有助于精确理解卷积神经网络中每个过滤器容易接受的视觉模式或视觉概念。
    • 可视化图像中类激活的热力图：有助于理解图像的哪个部分被识别为属于某个类别，从而可以定位图像中的物体。
    • 可视化中间激活
      • 对于给定输入，展示网络中各个卷积层和池化层输出的特征图（层的输出通常被称为该层的激活，即激活函数的输出）
      • 随着层数的加深，层所提取的特征变得越来越抽象。更高的层激活包含关于特定输入的信息越来越少，而关于目标的信息越来越多（本例中即图像的类别：猫或狗）。深度神经网络可以有效地作为信息蒸馏管道（information distillation pipeline），输入原始数据（本例中是RGB 图像），反复对其进行变换，将无关信息过滤掉（比如图像的具体外观），并放大和细化有用的信息（比如图像的类别）。
    • 可视化卷积神经网络的过滤器
      • 从空白输入图像开始，将梯度下降应用于卷积神经网络输入图像的值，其目的是让某个过滤器的响应最大化。得到的输入图像是选定过滤器具有最大响应的图像
      • 我们需要构建一个损失函数，其目的是让某个卷积层的某个过滤器的值最大化；然后，我们要使用随机梯度下降来调节输入图像的值，以便让这个激活值最大化。
    • 可视化类激活的热力图
      • 类激活图（CAM，class activation map）可视化，它是指对输入图像生成类激活的热力图。类激活热力图是与特定输出类别相关的二维分数网格，对任何输入图像的每个位置都要进行计算，它表示每个位置对该类别的重要程度。
      • 用“每个通道对类别的重要程度”对“输入图像对不同通道的激活强度”的空间图进行加权，从而得到了“输入图像对类别的激活强度”的空间图。

代码

  • r[i, sequence] = 1.

    r, sequence 的类型是ndarray

    • 例: sequence: [1, 9, 34, 230,], i: 0
    • 则: r的下标为0的行中的 下标为1,9,34,230的位置赋值为1
posted @ 2020-03-30 15:12  twfb  阅读(267)  评论(0)  编辑  收藏  举报