矩阵快速幂

这周学习了矩阵快速幂，就在这里记录下我的一下理解吧。

要学习矩阵快速幂，首先得先知道“矩阵”和“快速幂”的写法。

先说快速幂

顾名思义，快速幂就是快速算底数的n次幂。其时间复杂度为O(log₂N)，与朴素的O(N)相比效率有了极大的提高。           ——百度百科

以NOIP2013的麦森数为例题，讲一下快速幂

从文件中输入P（1000<P<3100000），计算2^P-1的位数和最后500位数字（用十进制高精度数表示）

本题显然要使用高精度运算。对2^P-1位数可以用公式log10(2^P-1)+1来求。因为2^P最后一位不可能为0，所以原式可化简为log10(2^P)+1=P*log10(2)+1。于是就能快速得到麦森数的位数了。

我们主要看求最后500位的运算。这显然要用到高精度。但是使用普通的高精度运算，时间复杂度就为P*500^2=2500P。对于最大的P=3100000，显然超时。那有没有更快的算法呢？

这就要牵扯到二进制了，二进制一直是很神奇的一个东西。

以十进制数5举例子，5的二进制为101，这可以通过取模然后反过来得到。看一下101是怎样表示5的。

二进制逢二进一。所以十位上的数就表示这个数有几个2，这就像十进制的十位表示这个数有几个10一样。所以像十进制一样往上推，百位上的数就表示这个数有几个2^2，千位上的数就表示这个数有几个2^3……那么根据这样，就可以看出，101=1*2^2+0*2^1+1*2^0=5。二进制数101就是这么表示十进制数5的。

知道了这个，我们再看回本题。指数P，我们不妨把它转化为一个二进制数。那么指数是二进制，幂就好求很多了。在二进制中，只有0或1，也就是只有“没有”或“有”这两种状态。不妨举个例子，求a^1010111(2)的值，该怎么做呢？我们把同底数幂相乘的公式倒过来，那么a^1010111=a^1000000(2)*a^10000(2)*a^100(2)*a^10(2)*a^1(2)。那么这里的每个值，都可以通过循环或者递归来求出。在循环中，对每个数进行判断，如果这一位的二进制数为0，那么就是“没有”，所以不乘入答案，去看下一位；如果这一位的二进制数为1，那么就是“有”，把这个数乘入答案，循环到下一位。于是就可以在O(log(n))的时间复杂度内实现幂运算了。

顺便再说一下快速乘，其实快速乘的代码跟快速幂非常像，把所有的乘号改成加号就可以实现快速乘了。运用的是乘法分配律。快速乘的时间复杂度也为O(log(n))。比起普通的O(1)的乘来说，快速乘是把所有的乘变成加法，避免了数值溢出，便于取模而不需要写高精度。这在后面的题目当中会用到。

#include <iostream>
#include <cstring>
#include <cmath>
using namespace std;

const int maxlen=500;
int p;
int a[maxlen+2],b[maxlen+2],c[maxlen+2];

void init() {
    cin>>p;
    //输出位数
    cout<<(int)(p*log10(2)+1)<<endl;
    memset(a,0,sizeof(a));
    memset(b,0,sizeof(b));
    a[1]=1;
    b[1]=2;
}

//高精度乘法
void chengfa(int aa[],int bb[]) {
    memset(c,0,sizeof(c));
    for (int i=1; i<=500; i++)
        for (int j=1; j<=501-i; j++) {
            c[i+j-1]+=aa[i]*bb[j];
            c[i+j]+=c[i+j-1]/10;
            c[i+j-1]%=10;
        }
}

//快速幂函数
void kasumi() {
    while (p) {
        if (p%2) {
            chengfa(a,b);
            memcpy(a,c,sizeof(c));
        }
        chengfa(b,b);
        memcpy(b,c,sizeof(c));
        p=p/2;
    }
}

void shuchu(int aa[]) {
    for (int i=499; i>=0; i--) {
        cout<<aa[i+1];
        if (i%50==0) cout<<endl;
    }
}

int main() {
    init();
    kasumi();
    a[1]--;
    shuchu(a);
    return 0;
}

接着讲矩阵

在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合，最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。
矩阵是高等代数学中的常见工具，也常见于统计分析等应用数学学科中。在物理学中，矩阵于电路学、力学、光学和量子物理中都有应用；计算机科学中，三维动画制作也需要用到矩阵。 矩阵的运算是数值分析领域的重要问题。将矩阵分解为简单矩阵的组合可以在理论和实际应用上简化矩阵的运算。对一些应用广泛而形式特殊的矩阵，例如稀疏矩阵和准对角矩阵，有特定的快速运算算法。

说白了，m*n的矩阵就是一个m行n列的二维数组，并不难构造，然而在运算中却有惊人的功效。先介绍矩阵的几个运算法则。

矩阵加法

对于两个列数、行数均相同的矩阵（也就是所谓的同型矩阵），才能进行加法运算。运算的结果也是一个与参与运算的两个矩阵行数、列数均相同的矩阵，它的第 i 行第 j 列的数就是两个矩阵第 i 行第 j 列数的和。举个例子，。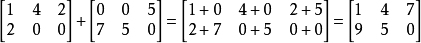

矩阵加法满足交换律和结合律。

加法比较简单。接下来说矩阵乘法。矩阵乘法可有点不一样。

两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。如A是m*n矩阵和B是n*p矩阵，它们的乘积C是一个m*p矩阵C=(c i,j)，它的一个元素：

并将此乘积记为C=AB。

也就是说，只有乘号前的矩阵的列数与乘号后矩阵的行数相同时，才能进行矩阵乘法运算。结果矩阵的第i行第j列的数，就是前矩阵的第i行上的所有数分别于后矩阵的第j列的所有数分别相乘的和。例如A为2*3的矩阵，B为3*3的矩阵，那么C应为2*3的矩阵。那么C[1][2]=A[1][1]*B[1][2]+A[1][2]*B[2][2]+A[1][3]*B[3][2]。举个实例：

。

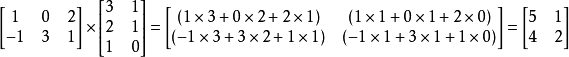矩阵乘法运算满足结合律（这个很经常用到），分配率。

不满足交换律！所以要注意了，做矩阵乘法时一定要细心，弄清楚哪一个矩阵在前，哪一个矩阵在后，不然就可能无法定义乘法运算，会出错。

矩阵乘法通过模拟，很容易实现，贴代码：

//计算a与b的矩阵积，a为n*m的矩阵，b为m*p的矩阵
//答案c应为一个n*p的矩阵 
for (int i=1; i<=n; i++)
    for (int j=1; j<=p; j++)
        for (int k=1; k<=m; k++)
            c[i][j]+=a[i][k]*b[k][j];

好了，既然知道了矩阵和快速幂，就可以开始讲矩阵快速幂了。所谓的矩阵快速幂，不仅仅是求一个矩阵的快速幂，常常是为了加速线型递推。每一个线型递推都可以使用矩阵快速幂的方法来加速。

先说矩阵如何实现快速幂。其实跟普通的快速幂差不多。只要把快速幂里面的乘法改成矩阵乘法就好了。为了数值传来传去的方便，我们可以定义一个结构体Matrix，里面仅包含一个二维数组mat，存储矩阵的值。因为结构体之间可以互相赋值，也可以作为函数的返回值，就显得方便许多了。

诶，等等，快速幂里不是有一个数是1吗？就是把这个矩阵所有元素都赋值为1吗？不对。根据乘法，任何一个实数乘1都得原数，有这样一个n*n的矩阵，它的左上——右下对角线都是1，其余数皆为0。拿任何一个n*n的矩阵乘这个矩阵，结果都得原矩阵，所以说这个矩阵就是矩阵中的1，称为“单位矩阵”。这就是矩阵快速幂的实现了。

那么矩阵快速幂是如何加速线型递推的呢？以这道模板题：斐波那契数列，为例说明。

题目描述

斐波那契数列:1,1,2,3,5,8,13……请你编程计算出第n项%1000000007的值(n<=10^15).

输入

一个整数n（n<=10^15）

输出

数列第n项的值

样例输入

4

样例输出

3

这题的n最大可达10^15，显然时间复杂度为O(n)的普通递推无法在1s内出解。需要把时间复杂度优化到对数级别的才能过，即需优化至O(log(n))。看到对数，第一反应就是快速幂运算。

我认为，用矩阵快速幂优化递推最难的一件事就是构造矩阵。我在这里记下我构造矩阵的方法。

先写出初始矩阵，和你想要得到的目标矩阵。一般来说，初始矩阵和目标矩阵都是一个1行n列的矩阵，这里n代表这个递推式有几项。初始矩阵中的每一项的值就是题目当中所给的已知数的值。而目标矩阵就是你想得到的矩阵，它跟初始矩阵需是同型矩阵，因为它要称为递推下一项的初始矩阵。比如本题，我可以定义一个最开始的初始矩阵为[1,1]，就是[F(1),F(2)]，那么我的目标矩阵就是[F(2),F(3)]。这时，我们把得出F(3)的过程写出来，目标矩阵就变为[F(2),F(1)+F(2)]。写好了初始矩阵和目标矩阵，我们就可以开始求需要进行幂运算的矩阵了。

进行幂运算的矩阵一般都是n*n的矩阵，这样才能使目标矩阵与初始矩阵为同型矩阵。根据矩阵乘法的运算法则，第一行第一列的数F(2)就等于初始矩阵的第一行[F(1),F(2)]乘需幂运算的矩阵的第一列[?,?]。显然，F(1)*0+F(2)*1=F(2)，故第一列确定下来为[0,1]。再看第二列。要得到的值是F(1)+F(2)，显然F(1)*1+F(2)*1=F(1)+F(2)=F(3)，所以第二列也被确定为[1,1]。那么需要幂运算的矩阵就这样简单地确定下来了，为[ (0,1) , (1,1) ]。

矩阵乘法满足结合律，于是就可以把后面那些每次递推所乘的相同的矩阵括号起来，计算这个矩阵的x次幂，再把初始矩阵与这个幂相乘，就可以快速得到结果了。用手算，模拟一下矩阵幂运算，即可算出x的值，即幂运算的指数。

但是有一个问题，在进行矩阵乘法运算时，矩阵的数值会出现溢出int的现象。这时候有两种处理方法。一种是把矩阵开成long long，然后及时取模。这种方法简单粗暴，代码量也小，且适用于本题，但是不适用于原本矩阵数值就为long long的情况。另一种方法，就是前面所说的快速乘，在每次循环中取模，就可以使得数值不溢出int。

代码：

#include <iostream>
#include <cstring>
using namespace std;

//取模的数
const int Mod=1000000007;
long long n;
struct Matrix {
    int mat[2][2];
};
//A是要快速幂的矩阵
//D是单位矩阵
//T是初始矩阵（表示结果的矩阵）
Matrix A,D,T;

void init() {
    cin>>n;
    A.mat[0][0]=0;
    A.mat[0][1]=A.mat[1][1]=A.mat[1][0]=1;
    //构造单位矩阵
    for (int i=0; i<2; i++)
        D.mat[i][i]=1;
    T.mat[0][0]=T.mat[0][1]=1;
}

//快速乘函数（不要在意函数名啦）
int chtholly(int x, int n) {
    int ans=0;
    while (n) {
        if (n&1)
            ans+=x;
        ans%=Mod;
        x=x+x;
        x%=Mod;
        n>>=1;
    }
    return ans;
}

//矩阵乘法函数
Matrix chengfa(Matrix x, Matrix y) {
    Matrix z;
    memset(z.mat,0,sizeof(z.mat));
    for (int i=0; i<2; i++)
        for (int j=0; j<2; j++)
            for (int k=0; k<2; k++)
                z.mat[i][j]=(z.mat[i][j]+chtholly(x.mat[i][k],y.mat[k][j]))%Mod;
    return z;
}

//快速幂函数
Matrix kasumi(long long high) {
    while (high) {
        if (high%2)
            D=chengfa(D,A);
        high/=2;
        A=chengfa(A,A);
    }
    return D;
}

int main() {
    init();
    //特判前两项
    if (n<=2) {
        cout<<"1"<<endl;
        return 0;
    }
    A=kasumi(n-2);
    T=chengfa(T,A);
    cout<<T.mat[0][1]<<endl;
    return 0;
}

再说一道例题：NOI2012 随机数生成器

题目描述

栋栋最近迷上了随机算法，而随机数是生成随机算法的基础。栋栋准备使用线性同余法（Linear Congruential Method）来生成一个随机数列，这种方法需要设置四个非负整数参数m,a,c,X[0],按照下面的公式生成出一系列随机数{X[n]}：X[n+1]=(aX[n]+c)mod m其中mod m表示前面的数除以m的余数。从这个式子可以看出，这个序列的下一个数总是由上一个数生成的。用这种方法生成的序列具有随机序列的性质，因此这种方法被广泛地使用，包括常用的C++和Pascal的产生随机数的库函数使用的也是这种方法。栋栋知道这样产生的序列具有良好的随机性，不过心急的他仍然想尽快知道X[n]是多少。由于栋栋需要的随机数是0,1,...,g-1之间的，他需要将X[n]除以g取余得到他想要的数，即X[n] mod g，你只需要告诉栋栋他想要的数X[n] mod g是多少就可以了。

输入

6个用空格分割的整数m,a,c,X[0],n和g，其中a,c,X[0]是非负整数，m,n,g是正整数。

100%的数据中n,m,a,c,X[0]<=10^18,g<=10^8。

输出

输出一个数，即X[n] mod g

样例输入

11 8 7 1 5 3

样例输出

2

这题应该如何构造矩阵呢？按照上面所述的方法，做出一个1行2列的矩阵，因为递推式“aX[n]+c”中有两项。第一项的跟前一个递推来的数有关，这里不妨把X[0]看做系数，a看做未知数。所以把矩阵的第一行第一列填上最开始的系数，也就是X[0]的值。矩阵的第二项是常数项，系数是1，所以就填上1。这样目标矩阵就是[ X[1], 1 ]。再把递推式融入，构造要实现快速幂的矩阵。第一行第一列的数X[1]是由a*X[0]+1*c得到的，所以就填入这两个单项式的未知数，a和c。于是矩阵的第一列就是[a,c]。第一行第二列的1，是由X[0]*0+1*1得到的，所以就在矩阵的第二列填上[0,1]。这样，矩阵就做好了。接着做快速幂就好了。

但是由于m在long long范围内，所以普通的乘法肯定会导致溢出。这时候就非得用快速乘不可了。

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
 
long long m,a,c,x,n,g;
struct Matrix {
    long long mat[3][3];
} A, D, T;
 
void init() {
    cin>>m>>a>>c>>x>>n>>g;
    A.mat[1][1]=a;
    A.mat[2][1]=c;
    A.mat[2][2]=1;
    D.mat[1][1]=D.mat[2][2]=1;
    T.mat[1][1]=x;
    T.mat[1][2]=1;
}
 
long long chtholly(long long x, long long n) {
    long long ans=0;
    while (n) {
        if (n&1)
            ans+=x;
        ans%=m;
        x=x+x;
        x%=m;
        n>>=1;
    }
    return ans;
}
 
Matrix chengfa(Matrix x, Matrix y) {
    Matrix z;
    memset(z.mat,0,sizeof(z.mat));
    for (int i=1; i<=2; i++)
        for (int j=1; j<=2; j++) {
            long long sum=0;
            for (int k=1; k<=2; k++) {
                sum+=chtholly(x.mat[i][k],y.mat[k][j]);
                sum%=m;
            }
            z.mat[i][j]=sum;
        }
    return z;
}
 
Matrix kasumi(long long high) {
    while (high) {
        if (high&1)
            D=chengfa(D,A);
        high>>=1;
        A=chengfa(A,A);
    }
    return D;
}
 
int main() {
    init();
    A=kasumi(n);
    T=chengfa(T,A);
    cout<<T.mat[1][1]%g<<endl;
    return 0;
}

矩阵还能做很多别的事。比如说VOJ1049——送给圣诞节的礼品。

描述

当小精灵们把贺卡都书写好了之后。礼品准备部的小精灵们已经把所有的礼品都制作好了。可是由于精神消耗的缘故，他们所做的礼品的质量越来越小，也就是说越来越不让圣诞老人很满意。可是这又是没有办法的事情。

于是圣诞老人把礼品准备部的小精灵们聚集起来，说明了自己的看法：“现在你们有n个礼品，其质量也就是降序排列的。那么为了使得这个礼品序列保持平均，不像现在这样很有规律的降序，我这里有一个列表。”
“列表共有m行，这m行都称作操作（不是序列），每一行有n个数字，这些数字互不相同而且每个数字都在1到n之间。一开始，礼品的序列就是现在礼品所处的位置，也就是说，一开始礼品的序列就是1、2、3、4……n；那么然后，我们看列表的第一行操作，设这一行操作的第i个数字为a[i]，那么就把原来序列中的第a[i]个礼物放到现在这个序列的第i的位置上，然后组成新的礼物序列。然后，看列表的第二行操作……、第三行操作……一直到最后一行操作，重复上面的操作。当最后一行的操作结束，组成了的序列又按照第一行来操作，然后第二行操作……第三行操作……一直循环下去，直到一共操作了k行为止。最后生成的这个序列就是我们最终礼品送给孩子们的序列了。大家明白了吗？”
“明白了！”
等圣诞老人一个微笑走后，大家却开始忙碌了。因为m值可能很大很大，而小精灵们的操作速度有限。所以可能在圣诞老人去送礼物之前完成不了这个任务。让他们很是恼火……

输入

第一行三个数，n，m和k。

接下来m行，每行n个数。

输出

一行，一共n个数，表示最终的礼品序列。n个数之间用一个空格隔开，行尾没有空格，需要回车。

样例输入

7 5 8
6 1 3 7 5 2 4
3 2 4 5 6 7 1
7 1 3 4 5 2 6
5 6 7 3 1 2 4
2 7 3 4 6 1 5

样例输出

2 4 6 3 5 1 7

这一题可以直接用矩阵来模拟物品的交换方法：先计算出m次交换后的结果，然后求这个矩阵的k/m次幂，最后单独计算k%m次交换即可。

#include <iostream>
#include <cstring>
using namespace std;

const int maxn=100;
const int maxm=10;
int n,m,k;
struct Matrix {
    int mat[maxn+1][maxn+1];
};
Matrix A[maxm+1], B, D, T;

void init() {
    cin>>n>>m>>k;
    for (int i=1; i<=n; i++)
        T.mat[1][i]=i;
    //预先算好每一次的交换的情况的矩阵
    for (int i=1; i<=m; i++)
        for (int j=1; j<=n; j++) {
            int x;
            cin>>x;
            A[i].mat[x][j]=1;
        }
    for (int i=1; i<=n; i++)
        D.mat[i][i]=1;
}

Matrix chengfa(Matrix x, Matrix y) {
    Matrix z;
    memset(z.mat,0,sizeof(z.mat));
    for (int i=1; i<=n; i++)
        for (int j=1; j<=n; j++)
            for (int ii=1; ii<=n; ii++)
                z.mat[i][j]+=x.mat[i][ii]*y.mat[ii][j];
    return z;
}

Matrix kasumi(int high) {
    while (high) {
        if (high&1)
            D=chengfa(D,B);
        high>>=1;
        B=chengfa(B,B);
    }
    return D;
}

void solve() {
    B=A[1];
    for (int i=2; i<=m; i++)
        B=chengfa(B,A[i]);
    if (k>=2*m)
        B=kasumi(k/m);
    for (int i=1; i<=k%m; i++)
        B=chengfa(B,A[i]);
    T=chengfa(T,B);
}

void print() {
    for (int i=1; i<=n; i++) {
        cout<<T.mat[1][i];
        if (i^n)
            cout<<" ";
        else
            cout<<endl;
    }
}

int main() {
    init();
    solve();
    print();
    return 0;
}

我只是粗略地记录了一下矩阵快速幂的用法。若有错误，望神犇指教。