哈密顿回路的多项式复杂度算法
今天听说了一篇很牛逼的论文,标题就把我吓到了:《Hamiltonian Cycle Problem is in P》。网址:https://arxiv.org/abs/2105.07608。
我怀着好奇的心情下载读了一下,大概读懂了它的算法意思,我简单地解释一下。
先从几个定义看起。

定义一大致意思说的就是对原图 \(G\) 建一个 \(n + 1\) 层的分层图 \(G'\),其中第 \(0\) 层和第 \(n\) 层只有一个节点 \(1\)(原文写的是任选一个节点 \(v\) 作为回路的起点和终点,根据习惯我就简单地当做是 \(1\) 号节点了),中间的 \(1\) 到 \(n - 1\) 层每层都有节点 \(2\) 到节点 \(n\) 这 \((n - 1)\) 个节点,于是一共有 \((n - 1) ^ 2 + 2\) 个节点。然后对于原图的每条边都在分层图每相邻两层的对应端点连边。
总结起来就是非常标准的分层图建法,除了一些小细节处理可以理解为常数优化以外和我们习惯的建图方法一样。我不知道这玩意儿官方名称是不是叫 hologram,但就感觉这个 “全息图” 的名字老帅了。
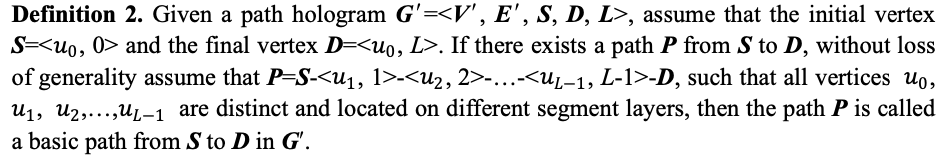
定义二说的就是一条从起点 \(<1, 0>\)(\(<u, l>\) 表示第 \(l\) 层的 \(u\) 号节点对应的节点,下同)到终点 \(<1, n>\) 的一条路径,除了起点终点经过的点都不相同。很容易发现如果把层那一维去掉,这条路径就是要求的一个哈密顿回路。

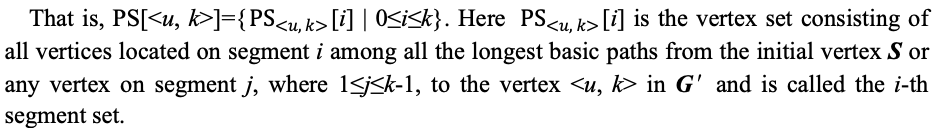
定义三比较有意思。它在分层图 \(G'\) 上的每一个点 \(<u, k>\) 定义了一个路径集合 \(\text{PS}[<u, k>]\)。这个数组里面记录了起点 \(<1, 0>\) 到这个点 \(<u, k>\) 上所有的路径。显然朴素的记录方法是 \(O(\)路径数\()\),不是多项式复杂度的,但是这里用了一个很“聪明”的方法:把每一层可能出现的点整理在一起合并起来。
举个例子,如果出现了这样的路径集合:\(\{(1, 2, 3, 4), (1, 2, 4, 3), (1, 3, 4, 2)\}\),那么对应的 \(\text{PS} = \{(1), (2, 3), (3, 4), (2, 3, 4)\}\)。因为第一个位置只出现了 \(1\),第二个位置出现了 \(2, 3\),第三个位置出现了 \(3, 4\),第四个位置出现了 \(2, 3, 4\)。这样一来就是多项式复杂度内的了。
如果你有做过哈密顿回路问题,应该能很明显的察觉出:PS 数组是没有意义的。事实上,这篇论文最大的问题就出在这里,请慢慢往下看。

定义四给了一些东西的简单记号。\(N ^ {-}(v)\) 表示原图上 \(v\) 点的入边集合,\(N ^ {+}(v)\) 表示原图上 \(v\) 点的出边集合。\(\text{PS}_{<u, k>}[i]\) 指的就是 \(\text{PS}[<u, k>]\) 这个集合数组,第 \(i\) 层的那个集合。\(AF ^ {-}(<v, i>)\) 和 \(AF ^ {+}(<v, i>)\) 我不知道怎么表述它,大概你根据那个定义理解一下,形象说一下就是这个点对路径记录的上一层的连通性的影响。
定义到这结束了。接下来它扔了几个结论,说是会在附录里证明它们。

结论一:原图存在哈密顿回路当且仅当分层图有那么一条路径。这个显然,拍扁了就是。这个结论没问题。
结论二:原图存在哈密顿回路当且仅当做完 PHG-BP 算法(PHG-BP 是作者给的该问题主算法的名字,全称为 Path HoloGram - Basic Path)后 \(\text{PS}[<1, n>]\) 非空。这个也没有问题。这个数组的定义就是所有能够到它的合法路径(合法指除了起点终点以外没有重复点)点集并起来,从定义出发就是正确的。但是这个 PHG-BG 算法是否真的能够求出 \(\text{PS}[<1, n>]\) 我表示怀疑。如果真的实现了,那么至少完成了在多项式时间内判断一张图是否有哈密顿回路,这成果不亚于找出哈密顿回路。
结论三到结论五都在说这个 PHG-BP 算法的正确性。其中 CM 算法(Consitency Maintain)和 LPM 算法(Longest Path Merging)都是 PHG-BP 算法中运用里调用的一些子函数。LPM 是非常简单的合并过程,但 CM 算法问题很大,接下来会详细介绍。
结论六说知道了 \(\text{PS}[<1, n>]\) 后可以用一个叫 FHC 算法(Find Hamilton Cycle)的东西路径还原得到哈密顿回路。这更离谱了,论文里给的算法问题非常明显,反例是很容易给出的,下文会介绍。
前置部分介绍完了,进入它主要的算法流程。
算法主要分为三大部分:GPHG(Generate Path HoloGram)、PHG-BP(Path HoloGram - Basic Path)和 FHC(Find Hamilton Cycle)。

GPHG 是简单的,就是普通的分层图建法。不赘述。
然后先来研究一下这个神奇的 FHC 函数。


我看到这直接大跌眼镜。原本以为有什么高妙的方法还原,实际上是这样的:从终点开始,选择一条非冗余的合法的前向边走过去,要求走到的节点 \(<v, i>\) 满足 \(v \in \text{PS}_{<1, n>}[i]\)(即 \(v\) 在可能出现的曼哈顿路径上)且还没有被加入过。
啊,槽点太多我不知道怎么说好。
要说复杂度是多项式的……的确。但是这个正确性……
算了直接扔个反例上来吧。
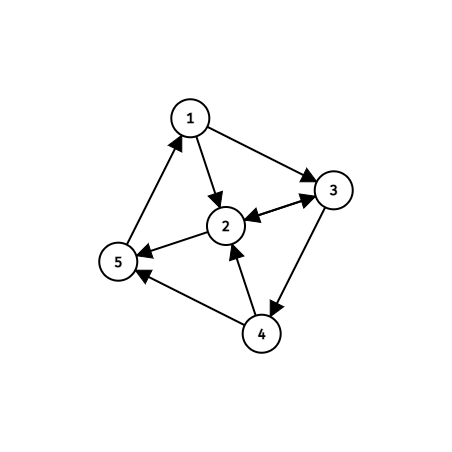
哈密顿路径有两条:\(1 \to 2 \to 3 \to 4 \to 5 \to 1\) 和 \(1 \to 3 \to 4 \to 2 \to 5 \to 1\)。所以 \(\text{PS} = \{(1), (2, 3), (3, 4), (2, 4), (5), (1)\}\)。当走到第三层(即 \(<2, 4>\) 层)的 \(2\) 时,如果刚好选到 \(3 \to 2\) 这条边走到了 \(3\),接下来立刻就无解了,找不出哈密顿回路。
最后看到这个最最最神奇的 PHG-BP 算法。

主函数就是一个 DP 的过程,从 \(<1, 0>\) 开始一层层往上推 \(\text{PS}\) 数组。有意思的在它的两个子函数 CM 和 LPM。
CM 函数的功能为,确定加入了这个新点 \(<u, i>\) 后,\(\text{PS}\) 数组(路径集合)会变成什么样。
LPM 函数的功能为,把这种情况的 \(\text{PS}\) 数组(路径集合)与已经求得的路径集合合并。
你可以理解为 DP 转移的过程。\(\texttt{f[u] = merge(f[u], plus(g[v], u))}\),其中 \(f\) 数组就是 \(\text{PS}\) 数组,\(\text{merge}\) 函数对应 \(\text{CM}\) 函数,而 \(\text{plus}\) 函数对应 \(\text{LPM}\) 函数。

LPM 比较正常。它做的事情就是把传进来两个 \(\text{PS}\) 数组各层的点集合并起来,没什么特殊的。我们着重关注 CM。

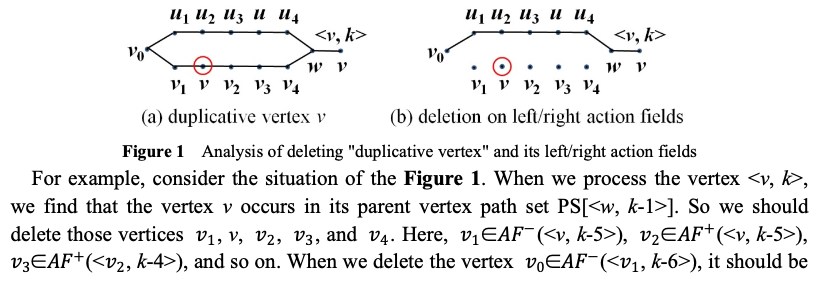



我们举加入一个点 \(<v, k>\) 为例。CM 函数分两类讨论。
一类是新加入的点 \(v\) 在之前的路径集合里出都没有出现过,这是最理想的情况,直接新开一个第 \(k\) 层给 \(v\) 就好。
否则出现过,那么出现了一些冲突。因为这一层只有 \(v\) 就说明这一层经过的点一定是 \(v\),那么 \(v\) 在之前的层里不能出现。这里麻烦可大了,用最浅白的话解释:出现了后效性。按照我们的认知,这个动态规划过程已经可以被否决掉了。可是这篇论文比较牛逼,它给出了一个调整 \(\text{PS}\) 数组的方法,可以多项式时间内退出新一步的 \(\text{PS}\) 数组。
调整法基于一个很肤浅的观察:第 \(k\) 层必须经过 \(v\) 点,那么前 \(k - 1\) 层所有有含 \(v\) 的路径全部都得删掉(可以参考论文中的图)。
可是怎么删呀?这时候最牛逼的函数出来了:LAFDR (Left Action Field Deleting-Replenishing)和 RAFDR(Right Action Field Deleting-Replenishing)。由于 RAFDR 和 LAFDR 对称,这里只介绍 LAFDR。
(可以这玩意该怎么介绍好啊?我完全无法理解它到底为什么可以这样做,直接根据伪代码看吧。具体的反例什么的先挖个坑待填吧。)
到这里论文最核心的东西讲完了。剩下那个 Conclusion 章节就说什么这个多项式算法适用性很广啊,价值很大啊,是一个 breakthrough 之类的。看着看着就笑了,笑着笑着就哭了。
怎么说呢?就觉得很厉害好吧。很厉害。






