边三连通分量算法

题目链接

给出一张 \(n\) 个点 \(m\) 条边的无向图，可能不连通、有重边、有自环、有割边。求其所有极大的边三连通分量。

\(n, m \le 5 \times 10 ^ 5\)。

论文太长了，还没看完，目前只看懂了算法步骤，一些证明还咕在后面。就先介绍一下步骤，正确性证明和时间复杂度证明等我看懂以后补上来。附一个论文原地址：A Simple 3-Edge-Connected Component Algorithm，来源选 ResearchGate 那个可以免费下载。本文内图片均出自这篇论文。

由于这个算法的核心在于其中的 Absort-Eject 操作，我习惯称其为 Absorb-Eject 算法。Absorb-Eject 算法的思想与求点双、边双的 Tarjan 算法类似，都是利用算法过程中建出的 dfs 树，求出点之间的连边情况。故为了更清晰地弄懂这个算法，最好对点双、边双的 Tarjan 算法有一定的理解。

为了减少讨论，我们需要先删除掉原图上一些可有可无，但会导致一些麻烦的分类情况的边：自环和割边。

• 自环：显然存在一个最优方案使得连通的三条路径都不包含自环，故自环可删。
• 边三连通分量一定是边双连通分量，因此割边两端的边不可能属于同一个边三连通分量，故割边可删。

经过这样预处理转化后，我们将原图变成了若干无自环的边双连通分量的连通块。那么以下的算法过程，均在这样的边双中进行。

首先，对限制条件进行一定的观察：两个点 \(u, v\) 在相同的边三内，当且仅当不存在一个边对 \((e_1, e_2)\)，满足将原图的 \(e_1, e_2\) 割开以后，\(u\) 与 \(v\) 不连通。

再加上这张图内没有割边，我们可以定义一个类似割边的定义：切边。我们称一条边 \(e\) 是切边，当且仅当它能够与另外一条边 \(e'\) 配合，把原图割成两个连通块。那么，对于一条边 \(e = (u, v)\)，若 \(e\) 是一条切边，则 \(u, v\) 一定不在一个相同的边三内；若 \(e\) 不是一条切边，则 \(u, v\) 一定在一个相同的边三内。所以我们只需要把原图中所有切边删去，剩下的边就将原图连成了若干边三。

于是我们明确了算法的目的：确定每条边是否为切边。

这个算法的核心步骤是 Absorb-Eject 操作，可译为吞吐操作。Absorb 会在一条边 \((w, u)\) 上进行，表示 \(w\) 将 \(u\) 吞并。吞并时，\(u\) 消失，所有与 \(u\) 相邻的边 \((x, u)\)（除了 \((w, u)\) 以外），都变成与 \(w\) 相邻的边 \((x, w)\)。特殊地，如果 \(u\) 的点度为 \(2\) （注意此时的点度是吞并后形成的新图的点度，而点 \(u\) 也可能已吞并了若干个点），那么可以割开这两条边使得 \(u\) 与外界不连通，说明 \(u\) 及 \(u\) 已吞并过的点是一个单独的边三，就让 \(w\) 将 \(u\) 吐出来，而吐出来的 \(u\) 失去所有相邻的边。

形式化来讲，对于每个点 \(u\)，定义其已吞并点集为 \(\sigma(u)\)，初始时，\(\sigma(u) = \{u\}\)。进行到目前的图为 \(G' = (V', E')\)，进行吞吐的边为 \((w, u)\)。那么进行一次 Absorb-Eject 操作后，图会变成 \(G' / e = (V'', E'')\)。其中 \(E'' = E' \setminus E_u \cup E_{w ^ +}\)，其中 \(E_u\) 表示 \(G'\) 中与 \(u\) 相邻的边，\(E_{w ^ +} = \{ f' = (w, z) \mid \exists f \in E_u,\text{ such that } f = (u, z) \text{ for some } z \in V' - \{w\} \}\)。而 \(V''\) 需要分类讨论，若 \(deg_{G'}(u) = 2\)，则 \(u\) 会被 \(w\) 吐出来，那么 \(V'\) 没变；若 \(deg_{G'}(u) \neq 2\)，则 \(u\) 被 \(w\) 吸收，\(V'' = V' - \{u\}\)，\(\sigma(w) = \sigma(w) \cup \sigma(u)\)。

由于可以证明（第一个待补证明的坑），若 \(deg_{G'}(u) \neq 2\)，则 \((w, u)\) 一定不是切边，也就是 \(w, u\) 一定在一个边三内。换句话说，就是 \(\sigma(w)\) 就是 \(w\) 所代表的一个原图上的一个边三。在进行若干次吞并后，所有的边都消失了，变成若干独立的点。则每个独立的点就代表着原图上一个极大边三连通分量，就是我们想求的东西。

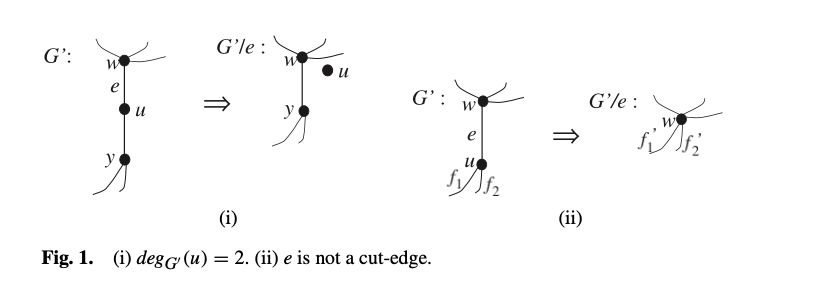
以上是核心步骤 Absorb-Eject。我们接下来用一个类似 Tarjan 算法的 dfs 过程，配合着 Absorb 操作，将原图一步步变成这样没有边的图，得到每一个表示极大边三连通分量的独立点。

又有一个奇怪的结论（第二个待补证明的坑）：递归完一个子树 \(u\) 结束回溯后，子树 \(u\) 内所有仍未确定是否为切边的边形成了一条一端为 \(u\) 的路径，也即修改后的图形成了一条一端为 \(u\) 的路径和若干代表者边三连通分量的独立点。我们称 \(u\) 上挂着的这条路径为 \(u\) - path，记 \(P_u\)，我们需要在 dfs 的过程中维护 \(P_u\)，最终到达根 \(r\) 时的 \(P_r\) 会为空，也就是再没有未确定是否为切边的边，就结束了我们的算法过程。

dfs 过程中，同样记录 \(low\) 和 \(dfn\)，\(dfn(u)\) 表示点 \(u\) 在 dfs 序中的编号，\(low(u)\) 表示 \(u\) 经过最多一条返祖边能到达的 \(dfn\) 最小值，那么有 \(low(w) = \min(\{low(u) \mid u \text{ is a child of } w\} \cup \{ dfn(w') \mid (w, w') \text{ is a back-edge} \} \cup \{dfn(w)\})\)。我们令此时 dfs 到了一个点 \(w\)，枚举其相邻边，分类讨论更新 \(low\) 和 \(P_w\)。

• \((w, u)\) 是一条没用的边，即 \(w = u\)，或 \((w, u)\) 为割边，或 \(u\) 是 \(w\) 的父亲且 \(w\) 是从 \(u\) 的这条边过来（就是父边）。不管，continue。
• \((w, u)\) 是一条树边。递归执行 \(dfs(u)\)。首先判断一下 \(deg_{G'}(u)\) 是否为 \(2\)，如果等于 \(2\) 那么要先把 \(u\) 独立吐出来形成一个单独的边三，同时把 \(u\) 从 \(P_u\) 中去掉，\(P_u = P_u - u\)。接着看 \(low(u)\) 是否会对 \(low(w)\) 产生贡献：
  • 若 \(low(u) < low(w)\)，大概由于增加了一条 \(u \to low(u) \to low(w) \to P_w\) 的路径，原本还未确定的 \(P_w\) 可以确定为不是切边了，于是让 \(w\) 将原本的 \(P_w\) 吞并掉，然后用 \(w + P_u\) 把 \(P_w\) 替换掉。
    
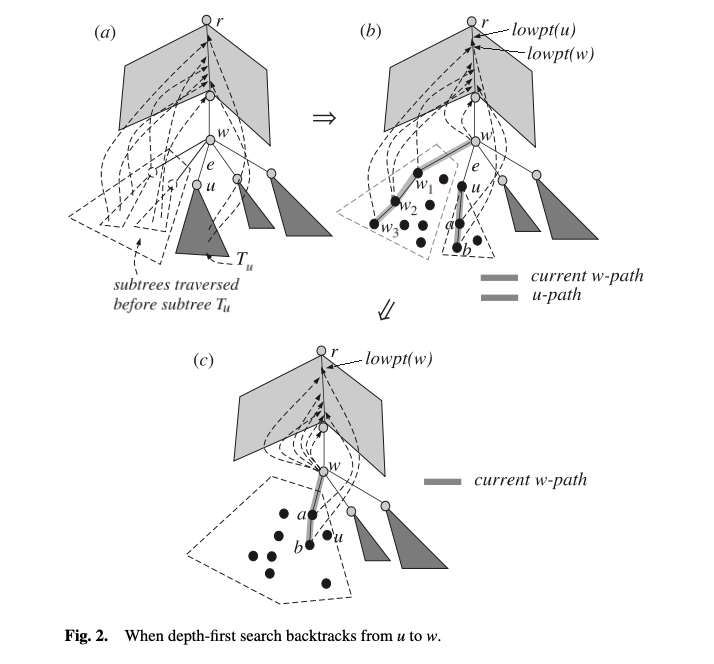
  • 若 \(low(u) \ge low(w)\)，类似上一条，原本还未确定的 \(P_u\) 可以确定为不是切边了，让 \(w\) 把 \(P_u\) 吞并掉，保持 \(P_w\) 不变。
• \((w, u)\) 是一条返祖边。若再满足 \(dfn(u)\) 可以更新 \(low(w)\)，那么 \(P_w\) 可以确定为不是切边了，这时让 \(w\) 把 \(P_w\) 吞并掉，然后 \(P_w\) 清空。
• \((w, u)\) 是一条前向边。由于 \((w, u)\) 这条边的存在，\(u\) 一定落在 \(P_w\) 上。那么这时 \(P_w\) 的 \([w \cdots u]\) 部分可以确定为不是切边了，就让 \(u\) 把 \(P_w\) 的 \([w \cdots u]\) 部分吞并掉，剪掉 \(P_w\) 的这段前缀。
  

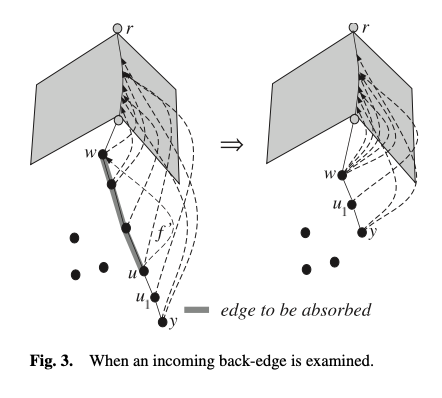
由于 \(low(r) = 1\)，所有的树边都会到 \(low(u) \ge low(w)\) 这条，因此 \(P_r\) 保持为空。也就是上面所说的，递归到根结束后，就确定了每条边是否为切边，算法顺利完成。

贴上论文中给出的伪代码：

最后，注意到图变化的时候边不需要显式地维护，只要维护每个点的相邻点度就好了。代码能比较容易地写出来。

我用了并查集维护一个点的集合，所以时间复杂度 \(\mathcal{O}((n + m) \log n)\)。实现细致一点可以把并查集扔掉，时间复杂度为 \(\mathcal{O}(n + m)\)。

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <utility>
#include <vector>

const int MaxN = 500000, MaxM = 500000;

struct graph_t {
  int cnte;
  int head[MaxN + 5], to[MaxM * 2 + 5], next[MaxM * 2 + 5];

  graph_t() { cnte = 1; }

  inline void addEdge(int u, int v) {
    cnte++; to[cnte] = v;
    next[cnte] = head[u]; head[u] = cnte;
  }
};

struct union_find {
  int par[MaxN + 5];
  union_find() { memset(par, -1, sizeof par); }

  int find(int x) { return par[x] < 0 ? x : par[x] = find(par[x]); }

  inline void merge(int u, int v) {
    int p = find(u), q = find(v);
    if (p == q) return;
    par[p] += par[q];
    par[q] = p;
  }
};

int N, M;
graph_t Gr;

class two_edge_connect {
private:
  int low[MaxN + 5], dfn[MaxN + 5], dfc;
  int stk[MaxN + 5], tp;
  int bel[MaxN + 5], s;

  void dfs(int u, int fe) {
    low[u] = dfn[u] = ++dfc;
    stk[++tp] = u;
    for (int i = Gr.head[u]; i; i = Gr.next[i]) {
      if ((i ^ fe) == 1) continue;
      int v = Gr.to[i];
      if (dfn[v] == 0) {
        dfs(v, i);
        low[u] = std::min(low[u], low[v]);
      } else
        low[u] = std::min(low[u], dfn[v]);
    }
    if (low[u] == dfn[u]) {
      s++;
      for (;;) {
        int v = stk[tp--];
        bel[v] = s;
        if (u == v) break;
      }
    }
  }

public:
  void init() {
    memset(dfn, 0, sizeof dfn);
    dfc = tp = s = 0;
    for (int i = 1; i <= N; ++i)
      if (dfn[i] == 0) dfs(i, 0);
  }

  inline bool isbridge(int u, int v) {
    return bel[u] != bel[v];
  }
};

class three_edge_connect {
private:
  two_edge_connect bcc;
  union_find uf;
  int low[MaxN + 5], dfn[MaxN + 5], end[MaxN + 5], dfc;
  int deg[MaxN + 5];

  inline bool insubtree(int u, int v) {
    if (dfn[u] <= dfn[v] && dfn[v] <= end[u]) return true;
    else return false;
  }

  inline void absorb(std::vector<int> &path, int u, int w = 0) {
    while (path.empty() == false) {
      int v = path.back();
      if (w > 0 && insubtree(v, w) == false) break;
      path.pop_back();
      deg[u] += deg[v] - 2;
      uf.merge(u, v);
    }
  }

  void dfs(int u, int fe, std::vector<int> &pu) {
    low[u] = dfn[u] = ++dfc;
    for (int i = Gr.head[u]; i; i = Gr.next[i]) {
      int v = Gr.to[i];
      if (u == v || bcc.isbridge(u, v) == true) continue;
      deg[u]++;
      if ((i ^ fe) == 1) continue;
      if (dfn[v] == 0) {
        std::vector<int> pv;
        dfs(v, i, pv);
        if (deg[v] == 2) pv.pop_back();
        if (low[v] < low[u]) {
          low[u] = low[v];
          absorb(pu, u);
          pu = pv;
        } else absorb(pv, u);
      } else {
        if (dfn[v] > dfn[u]) {
          absorb(pu, u, v);
          deg[u] -= 2;
        } else if (dfn[v] < low[u]) {
          low[u] = dfn[v];
          absorb(pu, u);
        }
      }
    }
    end[u] = dfc;
    pu.push_back(u);
  }

public:
  void init() {
    memset(dfn, 0, sizeof dfn);
    memset(deg, 0, sizeof deg);
    dfc = 0;
    bcc.init();
    for (int i = 1; i <= N; ++i) {
      if (dfn[i] == 0) {
        std::vector<int> pi;
        dfs(i, 0, pi);
      }
    }
  }

  std::vector< std::vector<int> > getall() {
    std::vector< std::vector<int> > res(N), ans;
    for (int i = 1; i <= N; ++i) {
      int x = uf.find(i);
      res[x - 1].push_back(i);
    }
    for (int i = 0; i < N; ++i)
      if (res[i].empty() == false) ans.push_back(res[i]);
    return ans;
  }
};

void init() {
  scanf("%d %d", &N, &M);
  for (int i = 1; i <= M; ++i) {
    int u, v;
    scanf("%d %d", &u, &v);
    Gr.addEdge(u, v);
    Gr.addEdge(v, u);
  }
}

inline bool cmp(const std::vector<int> &x, const std::vector<int> &y) { return x[0] < y[0]; }

void solve() {
  static three_edge_connect tcc;
  tcc.init();
  std::vector< std::vector<int> > ans = tcc.getall();
  for (int i = 0; i < (int) ans.size(); ++i)
    std::sort(ans[i].begin(), ans[i].end());
  std::sort(ans.begin(), ans.end(), cmp);
  printf("%d\n", (int) ans.size());
  for (int i = 0; i < (int) ans.size(); ++i) {
    int s = (int) ans[i].size();
    for (int j = 0; j < s; ++j)
      printf("%d%c", ans[i][j], " \n"[j == s - 1]);
  }
}

int main() {
  init();
  solve();
  return 0;
}