Delaunay 三角剖分
终于写完了,贴个代码先。题目是 公路修建。
只写了 Bowyer-Watson 和 Guibas-Stolfi。
Bowyer-Watson 在网上看了一圈找不到有 OI 选手写,看着一堆工程码风不知道是什么意思,只好自己琢磨,写了好久。写的时候还用到了在学 Guibas-Stolfi 时学到的,但没在 Guibas-Stolfi 里用到的 “三角形链表” 技巧。
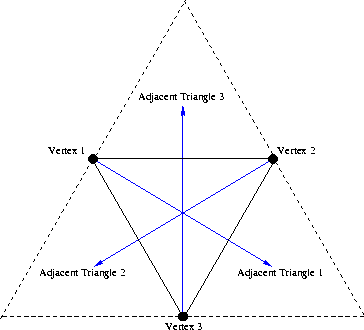
花了整整两天是写出来了,代码可读性几乎为零,而且常数特大。但网上说复杂度可以做到 \(\mathcal{O}(n \sqrt n)\),我就不知道怎么做。目前瓶颈在于:对于一张三角剖分好的图,求一个点在哪一个三角形内,要求复杂度不超过 \(\mathcal{O}(\sqrt n)\)。这玩意我只会 \(\mathcal{O}(n)\) 求。求各位大佬指教。
Bowyer-Watson:
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <utility>
#include <vector>
const int MaxN = 5005;
const int MaxF = 200000;
const double eps = 1e-9;
#ifdef Tweetuzki
#define debug(arg...) fprintf(stderr, arg)
#else
#define debug(arg...) void(0)
#endif
typedef struct vec_t {
double x, y;
vec_t(double _x = 0, double _y = 0) { x = _x, y = _y; }
inline friend vec_t operator+(const vec_t &a, const vec_t &b) { return vec_t(a.x + b.x, a.y + b.y); }
inline friend vec_t operator-(const vec_t &a, const vec_t &b) { return vec_t(a.x - b.x, a.y - b.y); }
inline friend vec_t operator*(const vec_t &a, double k) { return vec_t(a.x * k, a.y * k); }
inline friend double dot(const vec_t &a, const vec_t &b) { return a.x * b.x + a.y * b.y; }
inline friend double cross(const vec_t &a, const vec_t &b) { return a.x * b.y - a.y * b.x; }
inline friend double mod(const vec_t &a) { return sqrt(a.x * a.x + a.y * a.y); }
inline void shake() {
if (rand() % 2 == 0) x += 1.0 * rand() / RAND_MAX * eps;
else x -= 1.0 * rand() / RAND_MAX * eps;
if (rand() % 2 == 0) y += 1.0 * rand() / RAND_MAX * eps;
else y -= 1.0 * rand() / RAND_MAX * eps;
}
} node_t;
typedef struct vec3_t {
double x, y, z;
vec3_t(double _x = 0, double _y = 0, double _z = 0) { x = _x, y = _y, z = _z; }
inline friend vec3_t operator+(const vec3_t &a, const vec3_t &b) { return vec3_t(a.x + b.x, a.y + b.y, a.z + b.z); }
inline friend vec3_t operator-(const vec3_t &a, const vec3_t &b) { return vec3_t(a.x - b.x, a.y - b.y, a.z - b.z); }
inline friend vec3_t operator*(const vec3_t &a, double k) { return vec3_t(a.x * k, a.y * k, a.z * k); }
inline friend vec3_t cross(const vec3_t &a, const vec3_t &b) { return vec3_t(a.y * b.z - a.z * b.y, a.z * b.x - a.x * b.z, a.x * b.y - a.y * b.x); }
inline friend double dot(const vec3_t &a, const vec3_t &b) { return a.x * b.x + a.y * b.y + a.z * b.z; }
} node3_t;
struct triangle_t {
int a, b, c;
int la, lb, lc;
triangle_t(int _a = 0, int _b = 0, int _c = 0, int _la = 0, int _lb = 0, int _lc = 0) {
a = _a, b = _b, c = _c;
la = _la, lb = _lb, lc = _lc;
}
};
struct edge_t {
int u, v;
double w;
edge_t(int _u = 0, int _v = 0, double _w = 0) { u = _u, v = _v, w = _w; }
inline friend bool operator<(const edge_t &a, const edge_t &b) { return a.w < b.w; }
};
int N, CntF;
node_t A[MaxN + 5];
triangle_t F[MaxF + 5];
bool Del[MaxF + 5];
inline vec3_t mapping(const vec_t &a) { return vec3_t(a.x, a.y, a.x * a.x + a.y * a.y); }
inline bool inCircumcircle(const node_t &a, const node_t &b, const node_t &c, const node_t &p) {
node3_t _a = mapping(a), _b = mapping(b), _c = mapping(c), _p = mapping(p);
if (cross(b - a, c - a) < 0) std::swap(_b, _c);
node3_t normal = cross(_b - _a, _c - _a);
if (dot(normal, _p - _a) > eps) return false;
else return true;
}
inline bool inCircumcircle(const triangle_t &t, const node_t &p) { return inCircumcircle(A[t.a], A[t.b], A[t.c], p); }
void init() {
scanf("%d", &N);
for (int i = 1; i <= N; ++i) {
scanf("%lf %lf", &A[i].x, &A[i].y);
A[i].shake();
}
A[N + 1] = node_t(-1e6, -1e6), A[N + 2] = node_t(-1e6, 1e6);
A[N + 3] = node_t(1e6, -1e6), A[N + 4] = node_t(1e6, 1e6);
F[++CntF] = triangle_t(N + 1, N + 3, N + 2, 2, 0, 0);
F[++CntF] = triangle_t(N + 4, N + 2, N + 3, 1, 0, 0);
}
std::vector< std::pair<int, int> > Lk[MaxN + 5];
int To[MaxN + 5], Tof[MaxN + 5];
int NodeStk[MaxN + 5], NodeTp;
void dfs(int u, int f, int beg) {
debug("dfs(%d, %d, %d)\n", u, f, beg);
if (u == beg) {
if (f != 0) return;
NodeStk[NodeTp++] = u;
auto p = *(Lk[u].begin());
To[u] = p.first;
Tof[u] = p.second;
dfs(p.first, u, beg);
} else {
NodeStk[NodeTp++] = u;
for (auto p : Lk[u]) {
if (p.first == f) continue;
To[u] = p.first;
Tof[u] = p.second;
dfs(p.first, u, beg);
}
}
}
inline bool cmp(int a, int b, int c, int d) {
if (a == c && b == d) return true;
if (a == d && b == c) return true;
return false;
}
inline void insert(int insertNode) {
static int stk[MaxF + 5];
int tp = 0;
for (int i = 1; i <= CntF; ++i)
if (Del[i] == false && inCircumcircle(F[i], A[insertNode]) == true) {
stk[++tp] = i;
Del[i] = true;
}
for (int i = 1; i <= tp; ++i) debug("stk[%d] = %d\n", i, stk[i]);
static int e[MaxF + 5][3]; int cnte = 0;
for (int i = 1; i <= tp; ++i) {
int x = stk[i];
if (F[x].la == 0) {
cnte++;
e[cnte][0] = F[x].b, e[cnte][1] = F[x].c, e[cnte][2] = 0;
} else if (inCircumcircle(F[F[x].la], A[insertNode]) == false) {
int y = F[x].la;
cnte++;
if (F[y].la == x) {
F[y].la = -1;
e[cnte][0] = F[y].b, e[cnte][1] = F[y].c, e[cnte][2] = y;
} else if (F[y].lb == x) {
F[y].lb = -1;
e[cnte][0] = F[y].a, e[cnte][1] = F[y].c, e[cnte][2] = y;
} else {
F[y].lc = -1;
e[cnte][0] = F[y].a, e[cnte][1] = F[y].b, e[cnte][2] = y;
}
}
if (F[x].lb == 0) {
cnte++;
e[cnte][0] = F[x].a, e[cnte][1] = F[x].c, e[cnte][2] = 0;
} else if (inCircumcircle(F[F[x].lb], A[insertNode]) == false) {
int y = F[x].lb;
cnte++;
if (F[y].la == x) {
F[y].la = -1;
e[cnte][0] = F[y].b, e[cnte][1] = F[y].c, e[cnte][2] = y;
} else if (F[y].lb == x) {
F[y].lb = -1;
e[cnte][0] = F[y].a, e[cnte][1] = F[y].c, e[cnte][2] = y;
} else {
F[y].lc = -1;
e[cnte][0] = F[y].a, e[cnte][1] = F[y].b, e[cnte][2] = y;
}
}
if (F[x].lc == 0) {
cnte++;
e[cnte][0] = F[x].a, e[cnte][1] = F[x].b, e[cnte][2] = 0;
} else if (inCircumcircle(F[F[x].lc], A[insertNode]) == false) {
int y = F[x].lc;
cnte++;
if (F[y].la == x) {
F[y].la = -1;
e[cnte][0] = F[y].b, e[cnte][1] = F[y].c, e[cnte][2] = y;
} else if (F[y].lb == x) {
F[y].lb = -1;
e[cnte][0] = F[y].a, e[cnte][1] = F[y].c, e[cnte][2] = y;
} else {
F[y].lc = -1;
e[cnte][0] = F[y].a, e[cnte][1] = F[y].b, e[cnte][2] = y;
}
}
}
for (int i = 1; i <= cnte; ++i)
debug("e[%d] = (%d, %d, %d)\n", i, e[i][0], e[i][1], e[i][2]);
for (int i = 1; i <= cnte; ++i) {
Lk[e[i][0]].emplace_back(e[i][1], e[i][2]);
Lk[e[i][1]].emplace_back(e[i][0], e[i][2]);
}
NodeTp = 0;
dfs(e[1][0], 0, e[1][0]);
for (int i = 0; i < NodeTp; ++i)
debug("node = %d, to = %d, tof = %d\n", NodeStk[i], To[NodeStk[i]], Tof[NodeStk[i]]);
for (int i = 0; i < NodeTp; ++i) {
int id = CntF + (i % NodeTp) + 1;
F[id] = triangle_t(insertNode, NodeStk[i], To[NodeStk[i]], Tof[NodeStk[i]], CntF + ((i + 1) % NodeTp) + 1, CntF + ((i - 1 + NodeTp) % NodeTp) + 1);
if (Tof[NodeStk[i]] != 0) {
int y = Tof[NodeStk[i]];
if (F[y].la == -1 && cmp(NodeStk[i], To[NodeStk[i]], F[y].b, F[y].c)) F[y].la = id;
if (F[y].lb == -1 && cmp(NodeStk[i], To[NodeStk[i]], F[y].a, F[y].c)) F[y].lb = id;
if (F[y].lc == -1 && cmp(NodeStk[i], To[NodeStk[i]], F[y].a, F[y].b)) F[y].lc = id;
}
}
CntF += NodeTp;
for (int i = 0; i < NodeTp; ++i) Lk[NodeStk[i]].clear();
for (int i = 1; i <= CntF; ++i)
debug("i = %d, a = %d, b = %d, c = %d, la = %d, lb = %d, lc = %d, del = %d\n", i, F[i].a, F[i].b, F[i].c, F[i].la, F[i].lb, F[i].lc, Del[i]);
}
int CntE, Par[MaxN + 5];
edge_t ME[MaxF + 5];
int find(int x) { return x == Par[x] ? x : Par[x] = find(Par[x]); }
void solve() {
for (int i = 1; i <= N; ++i) insert(i);
for (int i = 1; i <= CntF; ++i)
if (Del[i] == false) debug("i = %d, a = %d, b = %d, c = %d, l = (%d, %d, %d)\n", i, F[i].a, F[i].b, F[i].c, F[i].la, F[i].lb, F[i].lc);
for (int i = 1; i <= N; ++i) Par[i] = i;
for (int i = 1; i <= CntF; ++i) {
if (F[i].a <= N && F[i].b <= N) ME[++CntE] = edge_t(F[i].a, F[i].b, mod(A[F[i].a] - A[F[i].b]));
if (F[i].a <= N && F[i].c <= N) ME[++CntE] = edge_t(F[i].a, F[i].c, mod(A[F[i].a] - A[F[i].c]));
if (F[i].b <= N && F[i].c <= N) ME[++CntE] = edge_t(F[i].b, F[i].c, mod(A[F[i].b] - A[F[i].c]));
}
std::sort(ME + 1, ME + 1 + CntE);
double ans = 0;
for (int i = 1; i <= CntE; ++i) {
int p = find(ME[i].u), q = find(ME[i].v);
if (p != q) {
Par[p] = q;
ans += ME[i].w;
}
}
printf("%.2lf\n", ans);
}
int main() {
#ifdef Tweetuzki
freopen("input.txt", "r", stdin);
freopen("output.txt", "w", stdout);
freopen("errorfile.txt", "w", stderr);
#endif
init();
solve();
return 0;
}
Guibas-Stolfi:
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
const int MaxN = 5000, MaxM = 100000;
const double eps = 1e-9;
#ifdef Tweetuzki
#define debug(arg...) fprintf(stderr, arg)
#else
#define debug(arg...) void(0)
#endif
typedef struct vec_t {
double x, y;
vec_t(double _x = 0, double _y = 0) { x = _x, y = _y; }
inline friend vec_t operator+(const vec_t &a, const vec_t &b) { return vec_t(a.x + b.x, a.y + b.y); }
inline friend vec_t operator-(const vec_t &a, const vec_t &b) { return vec_t(a.x - b.x, a.y - b.y); }
inline friend vec_t operator*(const vec_t &a, double k) { return vec_t(a.x * k, a.y * k); }
inline friend double dot(const vec_t &a, const vec_t &b) { return a.x * b.x + a.y * b.y; }
inline friend double cross(const vec_t &a, const vec_t &b) { return a.x * b.y - a.y * b.x; }
inline friend double mod(const vec_t &a) { return sqrt(a.x * a.x + a.y * a.y); }
inline void shake() {
if (rand() % 2 == 0) x += 1.0 * rand() / RAND_MAX * (1e-9);
else x -= 1.0 * rand() / RAND_MAX * (1e-9);
if (rand() % 2 == 0) y += 1.0 * rand() / RAND_MAX * (1e-9);
else y -= 1.0 * rand() / RAND_MAX * (1e-9);
}
} node_t;
typedef struct vec3_t {
double x, y, z;
vec3_t(double _x = 0, double _y = 0, double _z = 0) { x = _x, y = _y, z = _z; }
inline friend vec3_t operator+(const vec3_t &a, const vec3_t &b) { return vec3_t(a.x + b.x, a.y + b.y, a.z + b.z); }
inline friend vec3_t operator-(const vec3_t &a, const vec3_t &b) { return vec3_t(a.x - b.x, a.y - b.y, a.z - b.z); }
inline friend vec3_t cross(const vec3_t &a, const vec3_t &b) { return vec3_t(a.y * b.z - a.z * b.y, a.z * b.x - a.x * b.z, a.x * b.y - a.y * b.x); }
inline friend double dot(const vec3_t &a, const vec3_t &b) { return a.x * b.x + a.y * b.y + a.z * b.z; }
} node3_t;
struct Graph {
int cnte;
int head[MaxN + 5], to[MaxM * 2 + 5];
int pre[MaxM * 2 + 5], nxt[MaxM * 2 + 5];
Graph() {
cnte = 1;
memset(head, 0, sizeof head);
memset(to, 0, sizeof to);
memset(pre, 0, sizeof pre);
memset(nxt, 0, sizeof nxt);
}
inline void addEdge(int u, int v) {
cnte++;
to[cnte] = v;
nxt[cnte] = head[u];
pre[head[u]] = cnte;
head[u] = cnte;
}
inline void delEdge(int id) {
if (pre[id] != 0) nxt[pre[id]] = nxt[id];
if (nxt[id] != 0) pre[nxt[id]] = pre[id];
if (head[to[id ^ 1]] == id) head[to[id ^ 1]] = nxt[id];
}
};
struct edge_t {
int u, v;
double w;
edge_t(int _u = 0, int _v = 0, double _w = 0) { u = _u, v = _v, w = _w; }
inline friend bool operator<(const edge_t &a, const edge_t &b) { return a.w < b.w; }
};
int N, M;
node_t A[MaxN + 5], MemoryA[MaxN + 5];
int Indice[MaxN + 5];
int Par[MaxN + 5];
edge_t E[MaxM + 5];
Graph Gr;
inline node3_t mapping(const node_t &a) { return vec3_t(a.x, a.y, a.x * a.x + a.y * a.y); }
inline bool inCircumcircle(const node_t &a, const node_t &b, const node_t &c, const node_t &p) {
node3_t _a = mapping(a), _b = mapping(b), _c = mapping(c), _p = mapping(p);
if (cross(b - a, c - a) < 0) std::swap(_b, _c);
node3_t normal = cross(_b - _a, _c - _a);
if (dot(normal, _p - _a) > eps) return false;
else return true;
}
inline bool intersect(const node_t &a, const node_t &b, const node_t &c, const node_t &d) {
if (cross(c - a, b - a) * cross(b - a, d - a) < eps) return false;
if (cross(a - d, c - d) * cross(c - d, b - d) < eps) return false;
return true;
}
void init() {
srand(20040313U);
scanf("%d", &N);
for (int i = 1; i <= N; ++i) {
scanf("%lf %lf", &A[i].x, &A[i].y);
MemoryA[i] = A[i];
A[i].shake();
}
}
inline bool levelCompare(int x, int y) { return A[x].x < A[y].x; }
inline std::pair<int, int> getInitialBaseEdge(int l, int r) {
int m = (l + r) >> 1;
static int stk[MaxN + 5];
int tp = 0;
stk[++tp] = l, stk[++tp] = l + 1;
for (int i = l + 2; i <= r; ++i) {
while (tp > 1 && cross(A[Indice[stk[tp]]] - A[Indice[stk[tp - 1]]], A[Indice[i]] - A[Indice[stk[tp]]]) < eps) tp--;
stk[++tp] = i;
}
for (int i = 1; i < tp; ++i)
if (stk[i] <= m && stk[i + 1] > m) return std::make_pair(Indice[stk[i]], Indice[stk[i + 1]]);
return std::make_pair(-1, -1);
}
void fun(int l, int r) {
debug("fun(%d, %d)\n", l, r);
if (l == r) return;
if (l + 1 == r) {
Gr.addEdge(Indice[l], Indice[r]);
Gr.addEdge(Indice[r], Indice[l]);
return;
}
int m = (l + r) >> 1;
fun(l, m), fun(m + 1, r);
std::pair<int, int> base = getInitialBaseEdge(l, r);
for (;;) {
Gr.addEdge(base.first, base.second);
Gr.addEdge(base.second, base.first);
int leftFinal = -1, rightFinal = -1;
for (int i = Gr.head[base.first]; i; i = Gr.nxt[i]) {
int candidate = Gr.to[i];
if (cross(A[base.second] - A[base.first], A[candidate] - A[base.first]) < eps) continue;
if (leftFinal == -1 || inCircumcircle(A[base.first], A[base.second], A[leftFinal], A[candidate]) == true)
leftFinal = candidate;
}
for (int i = Gr.head[base.second]; i; i = Gr.nxt[i]) {
int candidate = Gr.to[i];
if (cross(A[candidate] - A[base.second], A[base.first] - A[base.second]) < eps) continue;
if (rightFinal == -1 || inCircumcircle(A[base.first], A[base.second], A[rightFinal], A[candidate]) == true)
rightFinal = candidate;
}
if (leftFinal == -1 && rightFinal == -1) break;
if (leftFinal != -1 && rightFinal != -1) {
if (inCircumcircle(A[base.first], A[base.second], A[leftFinal], A[rightFinal]) == true) leftFinal = -1;
else rightFinal = -1;
}
if (leftFinal != -1) {
for (int i = Gr.head[base.first]; i; i = Gr.nxt[i]) {
int linknode = Gr.to[i];
if (intersect(base.second, leftFinal, base.first, linknode) == true) {
Gr.delEdge(i);
Gr.delEdge(i ^ 1);
}
}
base = std::make_pair(leftFinal, base.second);
} else {
for (int i = Gr.head[base.second]; i; i = Gr.nxt[i]) {
int linknode = Gr.to[i];
if (intersect(base.first, rightFinal, base.second, linknode) == true) {
Gr.delEdge(i);
Gr.delEdge(i ^ 1);
}
}
base = std::make_pair(base.first, rightFinal);
}
}
}
int find(int x) { return x == Par[x] ? x : Par[x] = find(Par[x]); }
void solve() {
for (int i = 1; i <= N; ++i) Indice[i] = i;
std::sort(Indice + 1, Indice + 1 + N, levelCompare);
fun(1, N);
for (int u = 1; u <= N; ++u)
for (int i = Gr.head[u]; i; i = Gr.nxt[i]) {
int v = Gr.to[i];
if (u < v) {
debug("%d - %d\n", u, v);
E[++M] = edge_t(u, v, mod(MemoryA[v] - MemoryA[u]));
}
}
double ans = 0;
std::sort(E + 1, E + 1 + M);
for (int i = 1; i <= N; ++i) Par[i] = i;
for (int i = 1; i <= M; ++i) {
int u = E[i].u, v = E[i].v;
double w = E[i].w;
int p = find(u), q = find(v);
if (p != q) {
ans += w;
Par[p] = q;
}
}
printf("%.2lf\n", ans);
}
int main() {
#ifdef Tweetuzki
freopen("input.txt", "r", stdin);
freopen("output.txt", "w", stdout);
freopen("errorfile.txt", "w", stderr);
#endif
init();
solve();
return 0;
}






