LR Tightly-coupled Fusion of GPS in Optimization-based VIO

Abstract

提出一种融合GPS和视觉, 惯性测量在一个非线性优化的估计器.

系统状态的一个滑窗的最近状态会被估计, 通过最小化重投影误差, 相对惯性误差和全局位置误差.

我们用IMU预积分来形成惯性误差.

我们的方法持续的比松耦合的融合方法好. 相对位置误差少50%.

1. Introduction

更准确的GPS系统, 比如差分GPS, 是可能的但是他们需要基站.

[3, 4] 里用pose-graph优化融合了GPS. 但是, 这样的系统是松耦合的, 说明相对位姿估计是用VIO算法估计的, 而只是用pose graph优化align到全局坐标下.

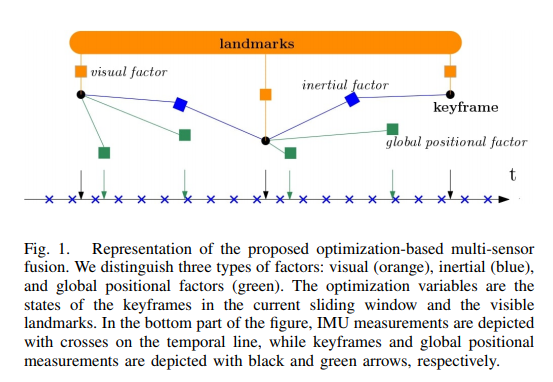
全局位置观测用来定义新的因子. 我们像[5]一样定义一个基于关键帧的滑窗优化, 主要的区别是加入了全局位置的因子, 状态量是不会有变化的.

因为全局误差项的框架, 计算量没啥变化, 比起VIO的情况.

A. Related Work

Filtering Methods:

滤波的方法有高效的估计, 通过只估计最近的状态. 很多基于滤波的方法, 融合了视觉和惯性测量的, 都是被[8]inspired, 提出了EKF.

[10]在线标定了IMU-GPS的外参和时延.

Smoothing Methods:

被分类为了 full 或者是 fixed-lag smoothers.

2. Problem Formulation

A. Notation

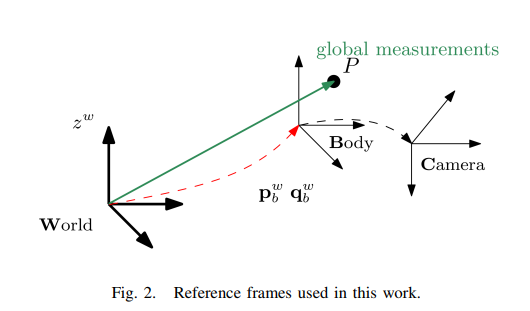
我们假设重力方向和\(z^w\) 是一致的.

全局位置估计是用 \(p_{p_k}^w\)的, 这里\(P\) 是跟\(B\)的一个刚体, 用 \(p_p^b\). 距离, 点 \(P\) 可以表示接收器天线的位置. 这里 \(p_p^b\) 可以通过标定获得.

滑窗优化的变量是: \(\mathcal{X} =\{\mathcal{L}, \mathcal{X}_B\}\).

B. Optimization-based Visual, Inertial, Global Information Fusion

cost function:

\[$J_{V I}(\mathcal{X})=\sum_{k=0}^{K-1} \sum_{j \in \mathcal{J}_{k}}\left\|\mathbf{e}_{\mathbf{v}}^{j, k}\right\|_{\mathbf{W}^{j, k}}^{2}+\sum_{k=0}^{K-1}\left\|\mathbf{e}_{\mathbf{i}}^{k}\right\|_{\mathbf{W}_{i}^{k}}^{2}+\left\|\mathbf{e}_{\mathbf{p}}\right\|^{2}$ \]

\(e_v\) 是视觉残差, \(e_i\) 是惯性残差, \(e_p\) 是边缘化残差?.

全局位置残差的推导是IMU预积分算法inspired.

误差项 \(e_p\) 表示从边缘化获得的prior information. 我们用了[5]里的边缘化策略. 即: 当一个新的帧插入了滑窗, 我们区分两种case.

1. 滑窗中的最老帧不是关键帧, 它会被边缘化, 它的landmark会被扔了.
2. 是的话, landmark也会被边缘化.

全局位置残差:

\[$J(\mathcal{X})=J_{V I}(\mathcal{X})+\sum_{k=0}^{K-1} \sum_{j \in \mathcal{G}_{k}}\left\|\mathbf{e}_{\mathbf{g}}^{j, k}\right\|_{\mathbf{W}_{\mathbf{g}}^{k}}^{2}$ \]

3. Derivation of Global Position Residuals

A. IMU Preintegration

我们用[17]提出的IMU预积分推导, 是基于持续时间的基于四元数的[18]和[7]中IMU偏置的操作.

IMU残差是用来约束连续状态,

用加速度计: \(\hat{\mathbf{a}}_{t}=\mathbf{a}_{t}+\mathbf{b}_{a_{t}}+\mathbf{R}_{w}^{t} \mathbf{g}^{w}+\mathbf{n}_{a}\)

用角速度计: \(\hat{\mathbf{w}}_{t}=\mathbf{w}_{t}+\mathbf{b}_{w_{t}}+\mathbf{n}_{w}\)

加速度计和陀螺仪的噪声是额外的高斯噪声:

加速度计: \(\mathbf{n}_{a} \sim \mathcal{N}\left(\mathbf{0}, \sigma_{a}^{2} \cdot \mathbf{I}\right)\)

角速度计: \(\mathbf{n}_{w} \sim \mathcal{N}\left(\mathbf{0}, \sigma_{w}^{2} \cdot \mathbf{I}\right)\)

偏置被model成随机游走:

加速度计: \(\dot{\mathbf{b}}_{a_{t}}=\eta_{b_{a}}\); \(\boldsymbol{\eta}_{b_{a}} \sim \mathcal{N}\left(\mathbf{0}, \sigma_{b_{a}}^{2} \cdot \mathbf{I}\right)\)

角速度计: \(\dot{\mathbf{b}}_{w_{t}}=\eta_{b_{w}}\); \(\boldsymbol{\eta}_{b_{w}} \sim \mathcal{N}\left(\mathbf{0}, \sigma_{b_{w}}^{2} \cdot \mathbf{I}\right)\)

---

给定时间段 \([t_k, t_{k+1}]\) , \(p, v, q\) 会在这个时间段上用加速度计, 角速度计传播.

在世界系下传播需要知道初始位姿, 这也暗含每次初始状态改变, 比如在优化的时候更新, 需要重新传播.

IMU预积分的主要好处就是每次更新后不需要重新传播.

传播是在local frame \(B_k\) 上的, 而不是世界系:

\[\begin{aligned} \mathbf{R}_{w}^{b_{k}} \mathbf{p}_{b_{k+1}}^{w} &=\mathbf{R}_{w}^{b_{w}}\left(\mathbf{p}_{b_{k}}^{w}+\mathbf{v}_{b_{k}}^{w} \Delta t_{k}-\frac{1}{2} \mathbf{g}^{w} \Delta t_{k}^{2}\right)+\boldsymbol{\alpha}_{b_{k+1}}^{b_{k}} \\ \mathbf{R}_{w}^{b_{k}} \mathbf{v}_{b_{k+1}}^{w} &=\mathbf{R}_{w}^{b_{k}}\left(\mathbf{v}_{b_{k}}^{w}-\mathbf{g}^{w} \Delta t_{k}\right)+\boldsymbol{\beta}_{b_{k+1}}^{b_{k}} \\ \mathbf{q}_{w}^{b_{k}} \otimes \mathbf{q}_{b_{k+1}}^{w} &=\gamma_{b_{k+1}}^{b_{k}} \end{aligned} \]

B. Global Position Residuals

全局位姿观测由 \(\{ p_{p_j}^w \}\) 给出, 我们model测量的不确定性是额外的高斯噪声.

\[\hat{\mathbf{p}}_{p_{j}}^{w}=\mathbf{p}_{p_{j}}^{w}+\mathbf{n}_{p} \]

给当前滑窗的一个状态 \(x_k\), 一个观测 \(\hat{p}_{p_j}^w\) 在时刻 \(t_j \in [ t_k, t_{k+1})\); 这个残差被定义为:

\[\mathbf{e}_{\mathbf{g}}^{j, k}=\mathbf{R}_{w}^{b_{k}}\left(\hat{\mathbf{p}}_{b_{j}}^{w}-\mathbf{p}_{b_{k}}^{w}-\mathbf{v}_{b_{k}}^{w} \Delta t_{k}+\frac{1}{2} \mathbf{g}^{w} \Delta t_{k}^{2}\right)-\hat{\boldsymbol{\alpha}}_{b_{j}}^{b_{k}} \]

这里测量 \(\hat{p}_{p_j}^w\) 转换到 \(\hat{p}_{b_j}^w\) :

\[\hat{\mathbf{p}}_{b_{j}}^{w}=\hat{\mathbf{p}}_{p_{j}}^{w}-\mathbf{R}_{b_{j}}^{w} \mathbf{p}_{p}^{b} \]

with \(\mathbf{R}_{b_{j}}^{w}=\mathbf{R}_{b_{k}}^{w} \hat{\gamma}_{j}^{k}\)

---

为了定义全局残差, 状态位置会有惯性测量在时间段 \([t_k, t_j]\) 传播.

为了推导残差的权重 \(\mathbf{W}^k_g\), 我们重写(7)作为:

\[\begin{aligned} \mathbf{e}_{\mathbf{g}}^{j, k}=& \mathbf{R}_{w}^{b_{k}}\left(-\mathbf{p}_{b_{k}}^{w}-\mathbf{v}_{b_{k}}^{w} \Delta t_{k}+\frac{1}{2} \mathbf{g}^{w} \Delta t_{k}^{2}\right) \\ &-\hat{\boldsymbol{\alpha}}_{b_{j}}^{b_{k}}+\mathbf{R}_{w}^{b_{k}} \hat{\mathbf{p}}_{p_{j}}^{w}-\mathbf{R}\left(\hat{\gamma}_{j}^{k}\right) \mathbf{p}_{p}^{b} \end{aligned} \]

在上式中, \(\hat{\boldsymbol{\alpha}}_{b_{j}}^{b_{k}}, \hat{\mathbf{p}}_{p_{j}}^{w} \text { and } \hat{\boldsymbol{\gamma}}_{j}^{k}\) 都是带噪声的测量. 协方差 \(\hat{\gamma}_j^k\) 是基于gyro的噪声和偏置. 因为gyro的噪声在 \(\hat{\alpha}_{b_j}^{b_k}\) 已经考虑了, 而且一般比加速度计噪声小很多, 所以在\(\mathbf{W}_g^k\) 的推导中忽视 \(\hat{\gamma}_j^k\) .

最终, 残差权重是基于 \(\hat{\boldsymbol{\alpha}}_{b_{j}}^{b_{k}}, \hat{\mathbf{p}}_{p_{j}}^{w}\)的

\[\mathbf{W}_{\mathbf{g}}^{k}=\hat{\boldsymbol{\alpha}} \mathbf{P}_{b_{j}}^{b_{k}}+\mathbf{R}_{w}^{b_{k}}\left(\sigma_{p}^{2} \cdot \mathbf{I}\right)\left(\mathbf{R}_{w}^{b_{k}}\right)^{t} \]

4. Experiment

A. EuRoC Dataset

立体图像是20Hz, IMU测量是200Hz.

Comparison to loosely-coupled:

5. Conclusion

没啥.