3.算法设计与分析__分治法
分治法目录
1 概 述
1.1 分治法的设计思想
将一个难以直接解决的大问题,划分成一些规模较小的子问题,以便各个击破,分而治之。更一般地说,将要求解的原问题划分成k个较小规模的子问题,对这k个子问题分别求解。如果子问题的规模仍然不够小,则再将每个子问题划分为k个规模更小的子问题,如此分解下去,直到问题规模足够小,很容易求出其解为止,再将子问题的解合并为一个更大规模的问题的解,自底向上逐步求出原问题的解。
启发式规则
- 平衡子问题:最好使子问题的规模大致相同。也就是将一个问题划分成大小相等的k个子问题(通常k=2),这种使子问题规模大致相等的做法是出自一种平衡(Balancing)子问题的思想,它几乎总是比子问题规模不等的做法要好。
- 独立子问题:各子问题之间相互独立,这涉及到分治法的效率,如果各子问题不是独立的,则分治法需要重复地解公共的子问题。
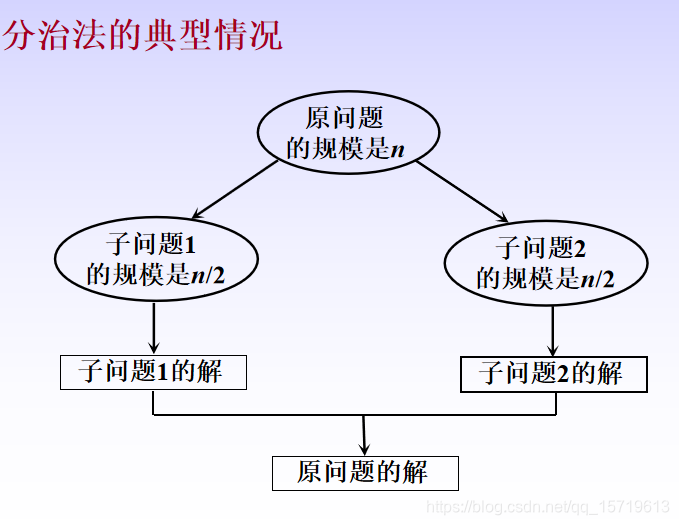
1.2 分治法的求解过程
一般来说,分治法的求解过程由以下三个阶段组成:
(1)划分:既然是分治,当然需要把规模为n的原问题划分为k个规模较小的子问题,并尽量使这k个子问题的规模大致相同。
(2)求解子问题:各子问题的解法与原问题的解法通常是相同的,可以用递归的方法求解各个子问题,有时递归处理也可以用循环来实现。
(3)合并:把各个子问题的解合并起来,合并的代价因情况不同有很大差异,分治算法的有效性很大程度上依赖于合并的实现。

2 递 归
2.1 递归的定义
递归(Recursion)就是子程序(或函数)直接调用自己或通过一系列调用语句间接调用自己,是一种描述问题和解决问题的基本方法。
递归有两个基本要素:
⑴ 边界条件:确定递归到何时终止;
⑵ 递归模式:大问题是如何分解为小问题的。
递归函数的经典问题——汉诺塔问题
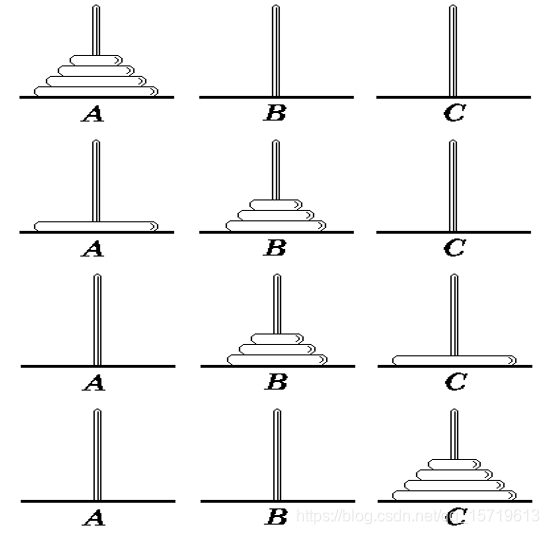
在世界刚被创建的时候有一座钻石宝塔(塔A),其上有64个金碟。所有碟子按从大到小的次序从塔底堆放至塔顶。紧挨着这座塔有另外两个钻石宝塔(塔B和塔C)。从世界创始之日起,婆罗门的牧师们就一直在试图把塔A上的碟子移动到塔C上去,其间借助于塔B的帮助。每次只能移动一个碟子,任何时候都不能把一个碟子放在比它小的碟子上面。当牧师们完成任务时,世界末日也就到了。
汉诺塔问题可以通过以下三个步骤实现:
(1)将塔A上的n-1个碟子借助塔C先移到塔B上。
(2)把塔A上剩下的一个碟子移到塔C上。
(3)将n-1个碟子从塔B借助塔A移到塔C上。
显然,这是一个递归求解的过程
void Hanoi(int n, char A, char B, char C)
//第一列为语句行号
{
if (n==1) Move(A, C);
//Move是一个抽象操作,表示将碟子从A移到C上
else {
Hanoi(n-1, A, C, B);
Move(A, C);
Hanoi(n-1, B, A, C);
}
}
2.2 递归函数的运行轨迹
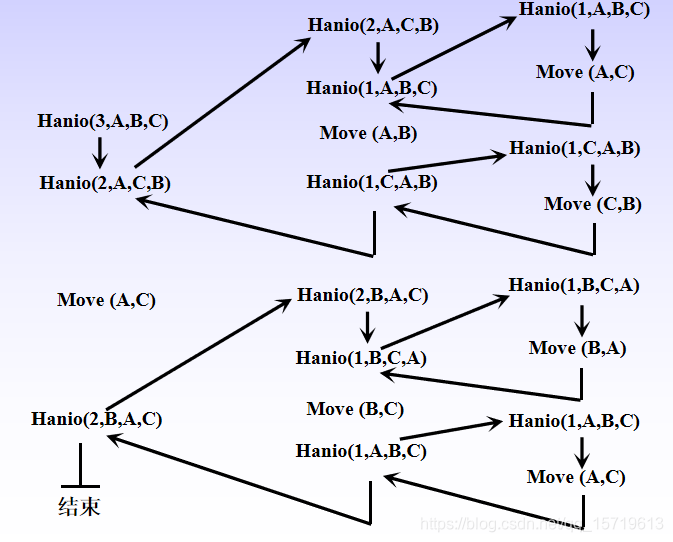
在递归函数中,调用函数和被调用函数是同一个函数,需要注意的是递归函数的调用层次,如果把调用递归函数的主函数称为第0层,进入函数后,首次递归调用自身称为第1层调用;从第i层递归调用自身称为第i+1层。反之,退出第i+1层调用应该返回第i层。采用图示方法描述递归函数的运行轨迹,从中可较直观地了解到各调用层次及其执行情况。
2.3 递归函数的内部执行过程
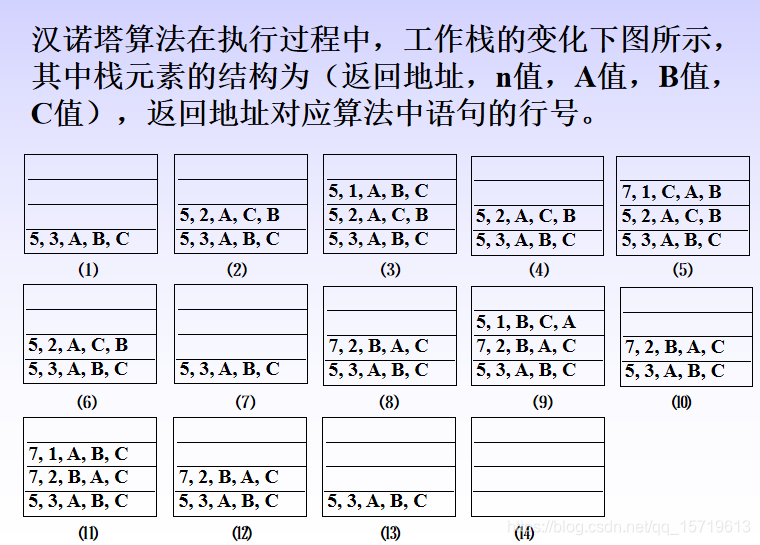
一个递归函数的调用过程类似于多个函数的嵌套调用,只不过调用函数和被调用函数是同一个函数。为了保证递归函数的正确执行,系统需设立一个工作栈。具体地说,递归调用的内部执行过程如下:
(1)运行开始时,首先为递归调用建立一个工作栈,其结构包括值参、局部变量和返回地址;
(2)每次执行递归调用之前,把递归函数的值参和局部变量的当前值以及调用后的返回地址压栈;
(3)每次递归调用结束后,将栈顶元素出栈,使相应的值参和局部变量恢复为调用前的值,然后转向返回地址指定的位置继续执行。
递归算法结构清晰,可读性强,而且容易用数学归纳法来证明算法的正确性,因此,它为设计算法和调试程序带来很大方便,是算法设计中的一种强有力的工具。但是,因为递归算法是一种自身调用自身的算法,随着递归深度的增加,工作栈所需要的空间增大,递归调用时的辅助操作增多,因此,递归算法的运行效率较低。
3 排序问题中的分治法
3.1 归并排序
二路归并排序的分治策略是
(1)划分:将待排序序列r1, r2, …, rn划分为两个长度相等的子序列r1, …, rn/2和rn/2+1, …, rn;
(2)求解子问题:分别对这两个子序列进行排序,得到两个有序子序列;
(3)合并:将这两个有序子序列合并成一个有序序列。
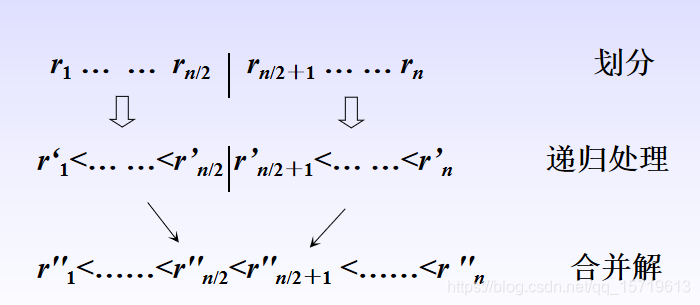
void MergeSort(int r[ ], int r1[ ], int s, int t)
{
if (s= =t) r1[s]=r[s];
else {
m=(s+t)/2;
Mergesort(r, r1, s, m); //归并排序前半个子序列
Mergesort(r, r1, m+1, t); //归并排序后半个子序列
Merge(r1, r, s, m, t); //合并两个已排序的子序列
}
}
二路归并排序的合并步的时间复杂性为O(n),所以,二路归并排序算法存在如下递推式:
根据1.2.4节的主定理,二路归并排序的时间代价是O(nlog2n)。
二路归并排序在合并过程中需要与原始记录序列同样数量的存储空间,因此其空间复杂性为O(n)。
void Merge(int r[ ], int r1[ ], int s, int m, int t)
{
i=s; j=m+1; k=s;
while (i<=m && j<=t)
{
if (r[i]<=r[j]) r1[k++]=r[i++]; //取r[i]和r[j]中较小者放入r1[k]
else r1[k++]=r[j++];
}
if (i<=m) while (i<=m)
//若第一个子序列没处理完,则进行收尾处理
r1[k++]=r[i++];
else while (j<=t)
//若第二个子序列没处理完,则进行收尾处理
r1[k++]=r[j++];
}
3.2 快速排序
快速排序的分治策略是
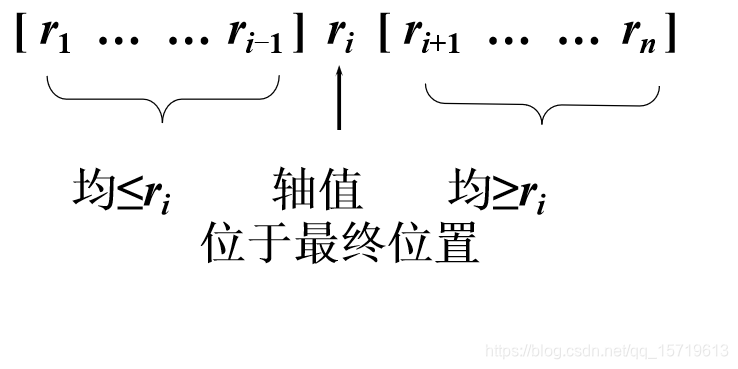
(1)划分:选定一个记录作为轴值,以轴值为基准将整个序列划分为两个子序列r1 … ri-1和ri+1 … rn,前一个子序列中记录的值均小于或等于轴值,后一个子序列中记录的值均大于或等于轴值;
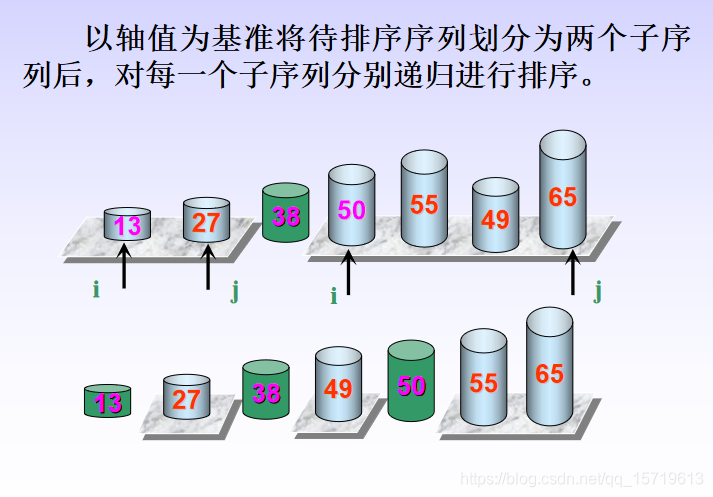
(2)求解子问题:分别对划分后的每一个子序列递归处理;
(3)合并:由于对子序列r1 … ri-1和ri+1 … rn的排序是就地进行的,所以合并不需要执行任何操作。
归并排序按照记录在序列中的位置对序列进行划分,
快速排序按照记录的值对序列进行划分。
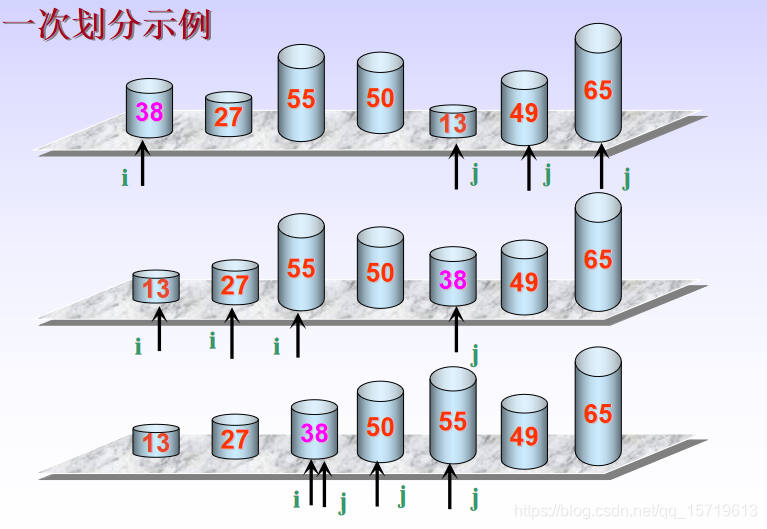
以第一个记录作为轴值,对待排序序列进行划分的过程为:
(1)初始化:取第一个记录作为基准,设置两个参数i,j分别用来指示将要与基准记录进行比较的左侧记录位置和右侧记录位置,也就是本次划分的区间;
(2)右侧扫描过程:将基准记录与j指向的记录进行比较,如果j指向记录的关键码大,则j前移一个记录位置。重复右侧扫描过程,直到右侧的记录小(即反序),若i<j,则将基准记录与j指向的记录进行交换;
(3)左侧扫描过程:将基准记录与i指向的记录进行比较,如果i指向记录的关键码小,则i后移一个记录位置。重复左侧扫描过程,直到左侧的记录大(即反序),若i<j,则将基准记录与i指向的记录交换;
(4)重复(2)(3)步,直到i与j指向同一位置,即基准记录最终的位置。
int Partition(int r[ ], int first, int end)
{
i=first; j=end; //初始化
while (i<j)
{
while (i<j && r[i]<= r[j]) j--; //右侧扫描
if (i<j) {
r[i]←→r[j]; //将较小记录交换到前面
i++;
}
while (i<j && r[i]<= r[j]) i++; //左侧扫描
if (i<j) {
r[j]←→r[i]; //将较大记录交换到后面
j--;
}
}
retutn i; // i为轴值记录的最终位置
}
void QuickSort(int r[ ], int first, int end)
{
if (first<end) {
pivot=Partition(r, first, end);
//问题分解,pivot是轴值在序列中的位置
QuickSort(r, first, pivot-1);
//递归地对左侧子序列进行快速排序
QuickSort(r, pivot+1, end);
//递归地对右侧子序列进行快速排序
}
}
在最好情况下,每次划分对一个记录定位后,该记录的左侧子序列与右侧子序列的长度相同。在具有n个记录的序列中,一次划分需要对整个待划分序列扫描一遍,则所需时间为O(n)。设T(n)是对n个记录的序列进行排序的时间,每次划分后,正好把待划分区间划分为长度相等的两个子序列,则有:
T(n)≤2 T(n/2)+n
≤2(2T(n/4)+n/2)+n=4T(n/4)+2n
≤4(2T(n/8)+n/4)+2n=8T(n/8)+3n
… … …
≤nT(1)+nlog2n=O(nlog2n)
因此,时间复杂度为O(nlog2n)。
在最坏情况下,待排序记录序列正序或逆序,每次划分只得到一个比上一次划分少一个记录的子序列(另一个子序列为空)。此时,必须经过n-1次递归调用才能把所有记录定位,而且第i趟划分需要经过n-i次关键码的比较才能找到第i个记录的基准位置,因此,总的比较次数为:

因此,时间复杂度为O(n2)。
在平均情况下,设基准记录的关键码第k小(1≤k≤n),则有:

这是快速排序的平均时间性能,可以用归纳法证明,其数量级也为O(nlog2n)。
4 组合问题中的分治法
4.1 最大子段和问题
给定由n个整数组成的序列(a1, a2, …, an),最大子段和问题要求该序列形如
的最大值(1≤i≤j≤n),当序列中所有整数均为负整数时,其最大子段和为0。例如,序列(-20, 11, -4, 13, -5, -2)的最大子段和为: 
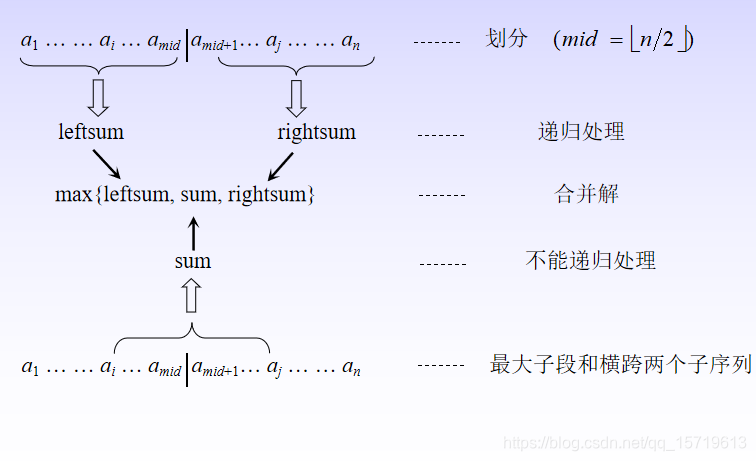
最大子段和问题的分治策略是:
(1)划分:按照平衡子问题的原则,将序列(a1, a2, …, an)划分成长度相同的两个子序列(a1, …, a )和(a +1, …, an),则会出现以下三种情况:
① a1, …, an的最大子段和=a1, …,a 的最大子段和;
② a1, …, an的最大子段和=a +1, …, an的最大子段和;
③ a1, …, an的最大子段和= 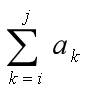 ,且
,且

(2)求解子问题:对于划分阶段的情况①和②可递归求解,情况③需要分别计算 

,则s1+s2为情况③的最大子段和。
(3)合并:比较在划分阶段的三种情况下的最大子段和,取三者之中的较大者为原问题的解。
int MaxSum(int a[ ], int left, int right)
{
sum=0;
if (left= =right) { //如果序列长度为1,直接求解
if (a[left]>0) sum=a[left];
else sum=0;
}
else {
center=(left+right)/2; //划分
leftsum=MaxSum(a, left, center);
//对应情况①,递归求解
rightsum=MaxSum(a, center+1, right);
//对应情况②,递归求解
s1=0; lefts=0; //以下对应情况③,先求解s1
for (i=center; i>=left; i--)
{
lefts+=a[i];
if (lefts>s1) s1=lefts;
}
s2=0; rights=0; //再求解s2
for (j=center+1; j<=right; j++)
{
rights+=a[j];
if (rights>s2) s2=rights;
}
sum=s1+s2; //计算情况③的最大子段和
if (sum<leftsum) sum=leftsum;
//合并,在sum、leftsum和rightsum中取较大者
if (sum<rightsum) sum=rightsum;
}
return sum;
}

4.2 棋盘覆盖问题
在一个2k×2k (k≥0)个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为特殊方格。棋盘覆盖问题要求用图4.11(b)所示的4种不同形状的L型骨牌覆盖给定棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。
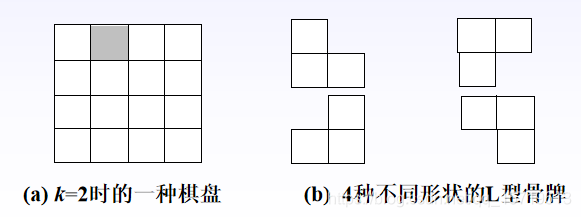
分治法求解棋盘覆盖问题的技巧在于划分棋盘,使划分后的子棋盘的大小相同,并且每个子棋盘均包含一个特殊方格,从而将原问题分解为规模较小的棋盘覆盖问题。
k>0时,可将2k×2k的棋盘划分为4个2k-1×2k-1的子棋盘,这样划分后,由于原棋盘只有一个特殊方格,所以,这4个子棋盘中只有一个子棋盘包含该特殊方格,其余3个子棋盘中没有特殊方格。为了将这3个没有特殊方格的子棋盘转化为特殊棋盘,以便采用递归方法求解,可以用一个L型骨牌覆盖这3个较小棋盘的会合处,从而将原问题转化为4个较小规模的棋盘覆盖问题。递归地使用这种划分策略,直至将棋盘分割为1×1的子棋盘。

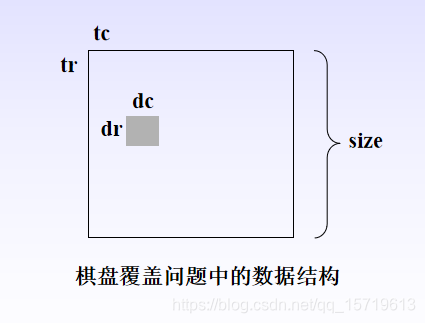
下面讨论棋盘覆盖问题中数据结构的设计。
(1)棋盘:可以用一个二维数组board[size][size]表示一个棋盘,其中,size=2k。为了在递归处理的过程中使用同一个棋盘,将数组board设为全局变量;
(2)子棋盘:整个棋盘用二维数组board[size][size]表示,其中的子棋盘由棋盘左上角的下标tr、tc和棋盘大小s表示;
(3)特殊方格:用board[dr][dc]表示特殊方格,dr和dc是该特殊方格在二维数组board中的下标;
(4) L型骨牌:一个2k×2k的棋盘中有一个特殊方格,所以,用到L型骨牌的个数为(4k-1)/3,将所有L型骨牌从1开始连续编号,用一个全局变量t表示。
void ChessBoard(int tr, int tc, int dr, int dc, int size)
// tr和tc是棋盘左上角的下标,dr和dc是特殊方格的下标,
// size是棋盘的大小,t已初始化为0
{
if (size = = 1) return; //棋盘只有一个方格且是特殊方格
t++; // L型骨牌号
s = size/2; // 划分棋盘
// 覆盖左上角子棋盘
if (dr < tr + s && dc < tc + s) // 特殊方格在左上角子棋盘中
ChessBoard(tr, tc, dr, dc, s); //递归处理子棋盘
else{ // 用 t 号L型骨牌覆盖右下角,再递归处理子棋盘
board[tr + s - 1][tc + s - 1] = t;
ChessBoard(tr, tc, tr+s-1, tc+s-1, s);
}
// 覆盖右上角子棋盘
if (dr < tr + s && dc >= tc + s) // 特殊方格在右上角子棋盘中
ChessBoard(tr, tc+s, dr, dc, s); //递归处理子棋盘
else { // 用 t 号L型骨牌覆盖左下角,再递归处理子棋盘
board[tr + s - 1][tc + s] = t;
ChessBoard(tr, tc+s, tr+s-1, tc+s, s); }
// 覆盖左下角子棋盘
if (dr >= tr + s && dc < tc + s) // 特殊方格在左下角子棋盘中
ChessBoard(tr+s, tc, dr, dc, s); //递归处理子棋盘
else { // 用 t 号L型骨牌覆盖右上角,再递归处理子棋盘
board[tr + s][tc + s - 1] = t;
ChessBoard(tr+s, tc, tr+s, tc+s-1, s); }
// 覆盖右下角子棋盘
if (dr >= tr + s && dc >= tc + s) // 特殊方格在右下角子棋盘中
ChessBoard(tr+s, tc+s, dr, dc, s); //递归处理子棋盘
else { // 用 t 号L型骨牌覆盖左上角,再递归处理子棋盘
board[tr + s][tc + s] = t;
ChessBoard(tr+s, tc+s, tr+s, tc+s, s); }
}

4.3 循环赛日程安排问题
设有n=2k个选手要进行网球循环赛,要求设计一个满足以下要求的比赛日程表:
(1)每个选手必须与其他n-1个选手各赛一次;
(2)每个选手一天只能赛一次。
按此要求,可将比赛日程表设计成一个 n 行n-1列的二维表,其中,第 i 行第 j 列表示和第 i 个选手在第 j 天比赛的选手。
按照分治的策略,可将所有参赛的选手分为两部分,n=2k个选手的比赛日程表就可以通过为n/2=2k-1个选手设计的比赛日程表来决定。递归地执行这种分割,直到只剩下2个选手时,比赛日程表的制定就变得很简单:只要让这2个选手进行比赛就可以了。
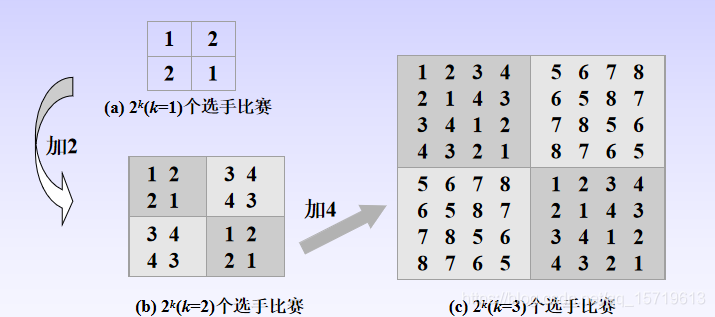
显然,这个求解过程是自底向上的迭代过程,其中左上角和左下角分别为选手1至选手4以及选手5至选手8前3天的比赛日程,据此,将左上角部分的所有数字按其对应位置抄到右下角,将左下角的所有数字按其对应位置抄到右上角,这样,就分别安排好了选手1至选手4以及选手5至选手8在后4天的比赛日程,如图©所示。具有多个选手的情况可以依此类推。
这种解法是把求解2k个选手比赛日程问题划分成依次求解21、22、…、2k个选手的比赛日程问题,换言之,2k个选手的比赛日程是在2k-1个选手的比赛日程的基础上通过迭代的方法求得的。在每次迭代中,将问题划分为4部分:
(1)左上角:左上角为2k-1个选手在前半程的比赛日程;
(2)左下角:左下角为另2k-1个选手在前半程的比赛日程,由左上角加2k-1得到,例如22个选手比赛,左下角由左上角直接加2得到,23个选手比赛,左下角由左上角直接加4得到;
(3)右上角:将左下角直接抄到右上角得到另2k-1个选手在后半程的比赛日程;
(4)右下角:将左上角直接抄到右下角得到2k-1个选手在后半程的比赛日程;
算法设计的关键在于寻找这4部分元素之间的对应关系。
void GameTable(int k, int a[ ][ ])
{
// n=2k(k≥1)个选手参加比赛,
//二维数组a表示日程安排,数组下标从1开始
n=2; //k=0,2个选手比赛日程可直接求得
//求解2个选手比赛日程,得到左上角元素
a[1][1]=1; a[1][2]=2;
a[2][1]=2; a[2][2]=1;
for (t=1; t<k; t++)
//迭代处理,依次处理22, …, 2k个选手比赛日程
{
temp=n; n=n*2;
//填左下角元素
for (i=temp+1; i<=n; i++ )
for (j=1; j<=temp; j++)
a[i][j]=a[i-temp][j]+temp;
//左下角元素和左上角元素的对应关系
//填右上角元素
for (i=1; i<=temp; i++)
for (j=temp+1; j<=n; j++)
a[i][j]=a[i+temp][(j+temp)% n];
//填右下角元素
for (i=temp+1; i<=n; i++)
for (j=temp+1; j<=n; j++)
a[i][j]=a[i-temp][j-temp];
}
}

5 几何问题中的分治法
5.1 最近对问题
设p1=(x1, y1), p2=(x2, y2), …, pn=(xn, yn)是平面上n个点构成的集合S,最近对问题就是找出集合S中距离最近的点对。
严格地讲,最接近点对可能多于一对,简单起见,只找出其中的一对作为问题的解。
用分治法解决最近对问题,很自然的想法就是将集合S分成两个子集 S1和 S2,每个子集中有n/2个点。然后在每个子集中递归地求其最接近的点对,在求出每个子集的最接近点对后,在合并步中,如果集合 S 中最接近的两个点都在子集 S1或 S2中,则问题很容易解决,如果这两个点分别在 S1和 S2中,问题就比较复杂了。
为了使问题易于理解,先考虑一维的情形。
此时,S中的点退化为x轴上的n个点x1, x2, …, xn。用x轴上的某个点m将S划分为两个集合S1和S2,并且S1和S2含有点的个数相同。递归地在S1和S2上求出最接近点对 (p1, p2) 和(q1, q2),如果集合S中的最接近点对都在子集S1或S2中,则d=min{(p1, p2), (q1, q2)}即为所求,如果集合S中的最接近点对分别在S1和S2中,则一定是(p3, q3),其中,p3是子集S1中的最大值,q3是子集S2中的最小值。

按这种分治策略求解最近对问题的算法效率取决于划分点m的选取,一个基本的要求是要遵循平衡子问题的原则。如果选取m=(max{S}+min{S})/2,则有可能因集合S中点分布的不均匀而造成子集S1和S2的不平衡,如果用S中各点坐标的中位数(即S的中值)作为分割点,则会得到一个平衡的分割点m,使得子集S1和S2中有个数大致相同的点。
下面考虑二维的情形,此时S中的点为平面上的点。
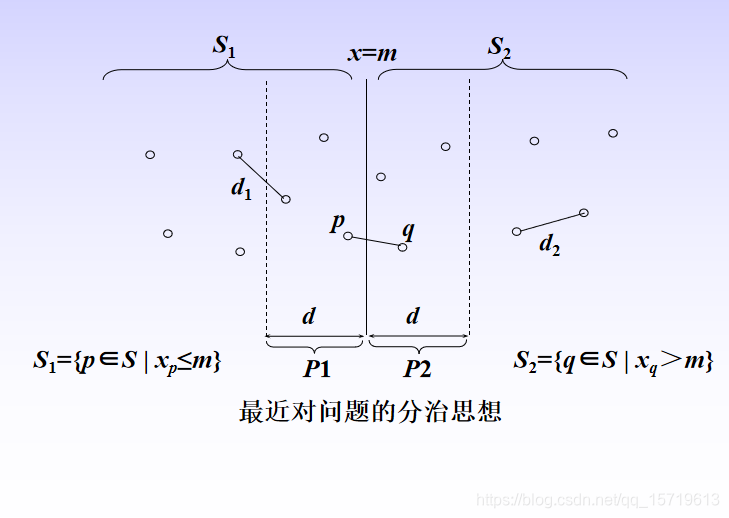
为了将平面上的点集S 分割为点的个数大致相同的两个子集S1和S2,选取垂直线x=m来作为分割线,其中,m为S中各点x坐标的中位数。由此将S分割为S1={p∈S | xp≤m}和S2={q∈S | xq>m}。递归地在S1和S2上求解最近对问题,分别得到S1中的最近距离d1和S2中的最近距离d2,令d=min(d1, d2),若S的最近对(p, q)之间的距离小于d,则p和q必分属于S1和S2,不妨设p∈S1,q∈S2,则p和q距直线x=m的距离均小于d,所以,可以将求解限制在以x=m为中心、宽度为2d的垂直带P1和P2中,垂直带之外的任何点对之间的距离都一定大于d。
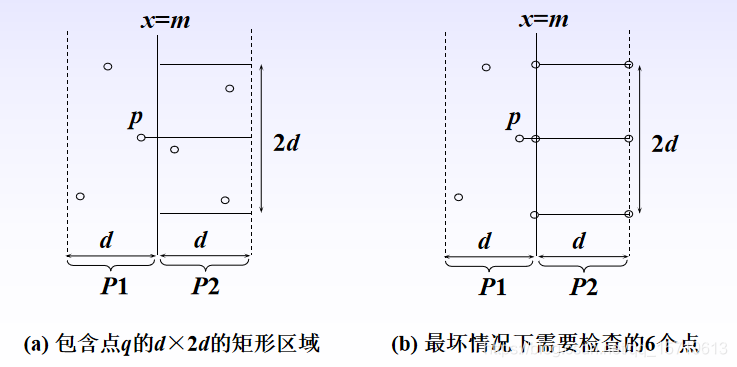
对于点p∈P1,需要考察P2中的各个点和点p之间的距离是否小于d,显然,P2中这样点的y轴坐标一定位于区间[y-d, y+d]之间,而且,这样的点不会超过6个。

5.2 凸包问题
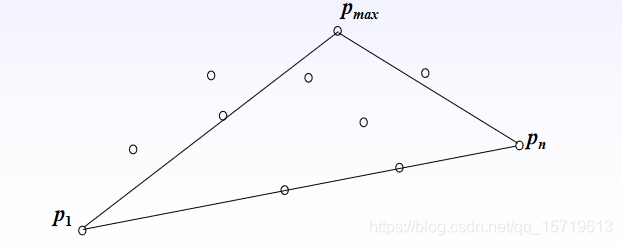
设p1=(x1, y1), p2=(x2, y2), …, pn=(xn, yn)是平面上n个点构成的集合S,并且这些点按照x轴坐标升序排列。几何学中有这样一个明显的事实:最左边的点p1和最右边的点pn一定是该集合的凸包顶点(即极点)。设p1pn是从p1到pn的直线,这条直线把集合S分成两个子集:S1是位于直线左侧和直线上的点构成的集合,S2是位于直线右侧和直线上的点构成的集合。S1的凸包由下列线段构成:以p1和pn为端点的线段构成的下边界,以及由多条线段构成的上边界,这条上边界称为上包。类似地,S2中的多条线段构成的下边界称为下包。整个集合S的凸包是由上包和下包构成的。
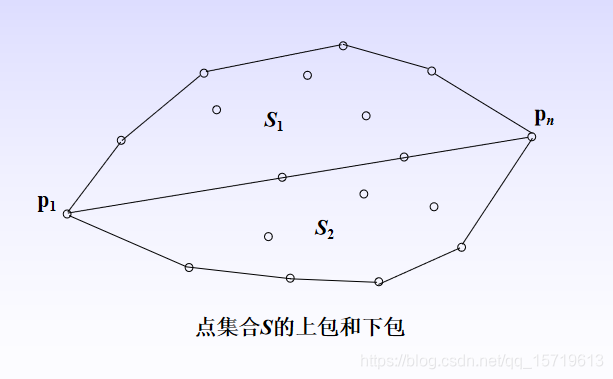
快包的思想是:首先找到S1中的顶点pmax,它是距离直线p1pn最远的顶点,则三角形pmaxp1pn的面积最大。S1中所有在直线pmaxp1左侧的点构成集合S1,1,S1中所有在直线pmaxpn右侧的点构成集合S1,2,包含在三角形pmaxp1pn之中的点可以不考虑了。递归地继续构造集合S1,1的上包和集合S1,2的上包,然后将求解过程中得到的所有最远距离的点连接起来,就可以得到集合S1的上包。
接下来的问题是如何判断一个点是否在给定直线的左侧(或右侧)?几何学中有这样一个定理:如果p1=(x1, y1), p2=(x2, y2), p3=(x3, y3)是平面上的任意三个点,则三角形p1p2p3的面积等于下面这个行列式的绝对值的一半:

当且仅当点p3=(x3, y3)位于直线p1p2的左侧时,该式的符号为正。可以在一个常数时间内检查一个点是否位于两个点确定的直线的左侧,并且可以求得这个点到该直线的距离。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号