注意力机制的数学公式梳理
本文为个人阅读笔记，参考《动手学深度学习》和蒲公英书《神经网络与深度学习》，两本书对RNN和attention都有简洁明了的介绍，深入浅出。
RNN回顾
循环神经网络使用隐状态\(h_{t-1}\)存储到时间步t-1的序列信息：
\(P\left(x_t \mid x_{t-1}, \ldots, x_1\right) \approx P\left(x_t \mid h_{t-1}\right)\)
时间步\(t\)的隐状态可以用当前输入\(x_t\)和先前隐状态\(h_{t−1}\)来计算：
\(h_t=f\left(x_t, h_{t-1}\right)\)
有许多不同的方法构建循环神经网络，最常见的隐状态计算方式：
\(\mathbf{H}_t=\phi\left(\mathbf{X}_t \mathbf{W}_{x h}+\mathbf{H}_{t-1} \mathbf{W}_{h h}+\mathbf{b}_h\right)\)
输出层则类似于多层感知机中的计算：
\(\mathbf{0}_t=\mathbf{H}_t \mathbf{W}_{h q}+\mathbf{b}_q\)
循环神经网络存在梯度爆炸和梯度消失、只能建立短距离依赖关系和局部编码，且无法并行计算；使用全连接网络可以直接建模远距离依赖，但无法处理变长的输入序列、根据输入长度改变连接权重的大小。利用注意力机制可以有效解决。
注意力
比起RNN这种token-by-token的时序处理方式，注意力机制采用一种“软性”的信息选择机制，对所有输入信息进行加权平均，其选择的信息是所有输入向量在注意力分布下的期望：
\(\begin{aligned} \operatorname{att}(\boldsymbol{X}, \boldsymbol{q}) & =\sum_{n=1}^N \alpha_n \boldsymbol{x}_n \\ & =\mathbb{E}_{\boldsymbol{p}(z \mid \boldsymbol{X}, \boldsymbol{q})}\left[\boldsymbol{x}_z\right]\end{aligned}\)
其中，\(\boldsymbol{X}=[\boldsymbol{x}_1, \boldsymbol{x}_2, \dots, \boldsymbol{x}_N] \in \mathbb{R}^{d \times N}\) 是一个包含 \(N\) 个元素的向量序列，\(\boldsymbol{q} \in \mathbb{R}^{d}\) 是一个查询向量，\(\alpha_n\) 是第 \(n\) 个元素的权重，满足 \(\sum_{n=1}^{N} \alpha_n = 1\)。期望值 \(\mathbb{E}_{\boldsymbol{p}(z \mid \boldsymbol{X}, \boldsymbol{q})}[\boldsymbol{x}_z]\)中\(z\) 表示被选择信息的索引位置。
这个模型可以通过控制注意力分布 \(\alpha_n\) 来使查询向量 \(\boldsymbol{q}\) 更加关注向量序列 \(\boldsymbol{X}\) 中的特定元素，从而更好地处理信息。
注意力分布\(\alpha_n\) 计算方式为：
\(\begin{aligned} \alpha_n & =p(z=n \mid \boldsymbol{X}, \boldsymbol{q}) \\ & =\operatorname{softmax}\left(s\left(\boldsymbol{x}_n, \boldsymbol{q}\right)\right) \\ & =\frac{\exp \left(s\left(\boldsymbol{x}_n, \boldsymbol{q}\right)\right)}{\sum_{j=1}^N \exp \left(s\left(\boldsymbol{x}_j, \boldsymbol{q}\right)\right)}\end{aligned}\)
其中，\(s(\boldsymbol{x}_n, \boldsymbol{q})\) 是注意力打分函数，用来衡量 \(\boldsymbol{x}_n\) 和查询向量 \(\boldsymbol{q}\) 之间相似度，可以用加性模型、点积模型、缩放点积模型、或双线性模型计算。
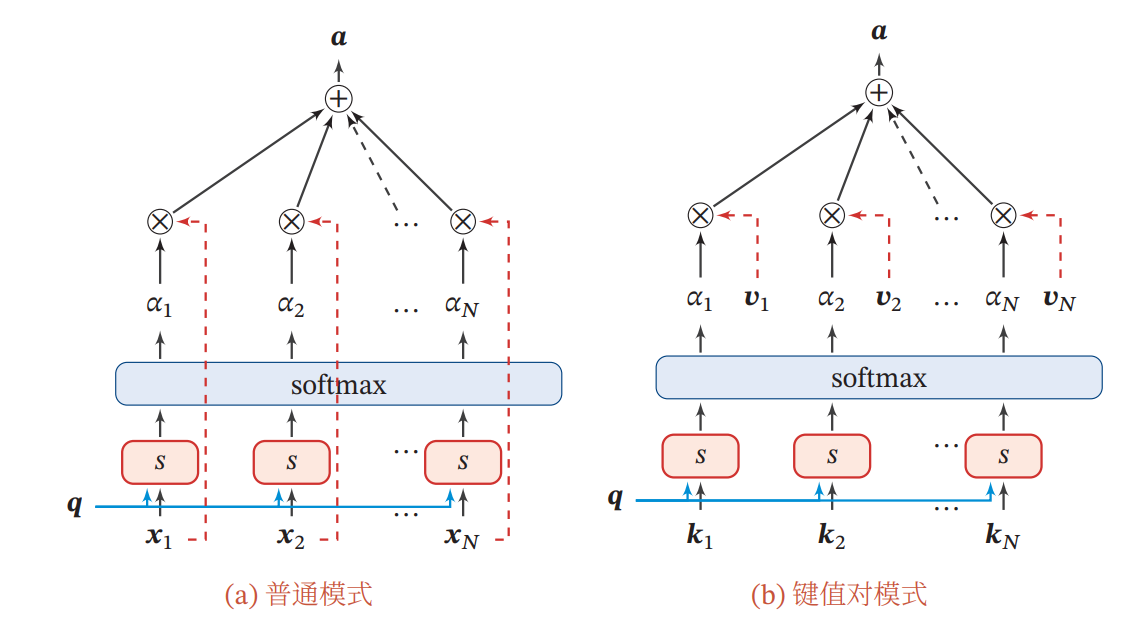
键值对注意力
以上是普通的注意力机制（\(\boldsymbol{K}=\boldsymbol{V}\)），更常用的键值对注意力函数如下：
\(\begin{aligned} \operatorname{att}((\boldsymbol{K}, \boldsymbol{V}), \boldsymbol{q}) & =\sum_{n=1}^N \alpha_n \boldsymbol{v}_n \\ & =\sum_{n=1}^N \frac{\exp \left(s\left(\boldsymbol{k}_n, \boldsymbol{q}\right)\right)}{\sum_j \exp \left(s\left(\boldsymbol{k}_j, \boldsymbol{q}\right)\right)} \boldsymbol{v}_n,\end{aligned}\)
使用注意力机制的优点是可以处理输入序列中的重要部分，削减噪声部分，提高计算效率。对于翻译任务，一个词的翻译应该与原句子中的特定词汇相关，而不是与整个句子相关，因此利用注意力机制使代表原/目标语的端到端模型表现更加优秀。
多头注意力
Transformer中用到的多头注意力能并行地从输入信息中选取多组信息：
\(\operatorname{att}((\boldsymbol{K}, \boldsymbol{V}), \boldsymbol{Q})=\operatorname{att}\left((\boldsymbol{K}, \boldsymbol{V}), \boldsymbol{q}_1\right) \oplus \cdots \oplus \operatorname{att}\left((\boldsymbol{K}, \boldsymbol{V}), \boldsymbol{q}_M\right)\)
其中\(\boldsymbol{Q}=[\boldsymbol{q}_1, \boldsymbol{q}_2, \dots, \boldsymbol{q}_M]\) 表示 \(M\) 个查询集合，每个查询集合具有相同的维度，即 \(\boldsymbol{q}_i \in \mathbb{R}^{d_q}\)。\(\operatorname{att}\left((\boldsymbol{K}, \boldsymbol{V}), \boldsymbol{q}_i\right)\) 表示第 \(i\) 个查询集合和 \((\boldsymbol{K}, \boldsymbol{V})\) 的注意力表示， \(\oplus\) 表示向量拼接。在这个公式中，多个查询 \(\boldsymbol{Q}\) 是用来探索数据中丰富性的。具体来讲，通过利用多个不同的查询向量 \(\boldsymbol{q}_i\)，多头注意力机制可以在不同的方向上关注不同的特征。
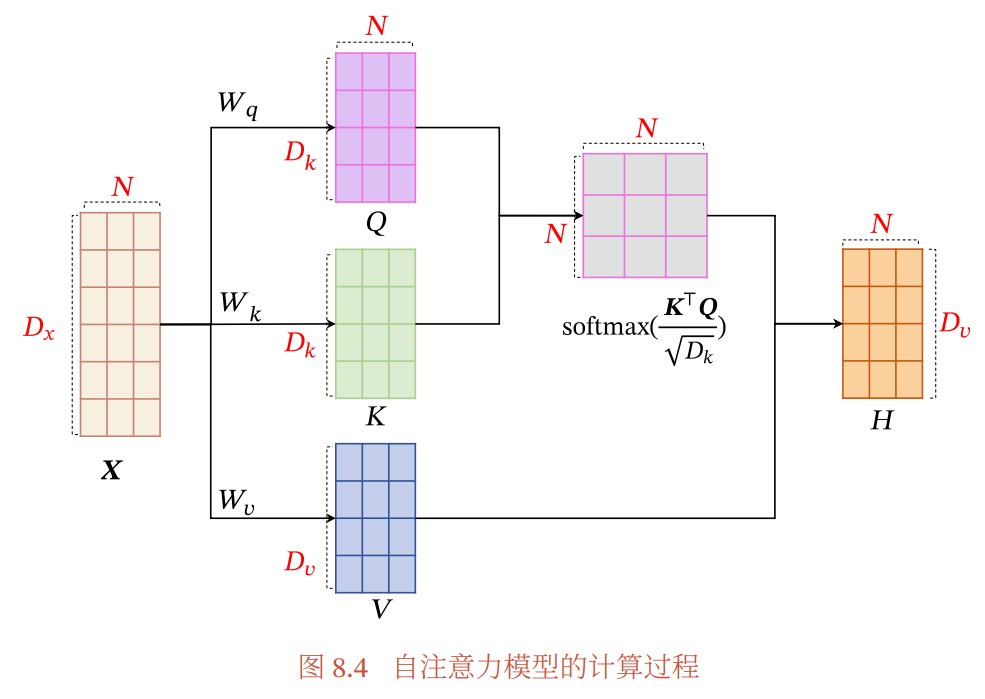
自注意力
相比普通的全连接模型，自注意力模型可以动态生成连接的权重。
对于整个输入序列 \(\boldsymbol{X}\), 将其线性映射到三个不同的空间：
\(Q=\left[q_1, \cdots, q_N\right], K=\left[k_1, \cdots, \boldsymbol{k}_N\right], \boldsymbol{V}=\left[\boldsymbol{v}_1, \cdots, \boldsymbol{v}_N\right]\) 分别是由查询向量、键向量和值向量构成的三个投影矩阵.
如果使用缩放点积来作为注意力打分函数, 输出向量序列为：
\(𝐷_𝑘\) 是矩阵𝑸 和𝑲 中列向量的维度.
