数据的离散化
在平常的题目当中,我们偶尔会遇上这种情况:给出了50000个数,数的范围是0-999999999;我们在题目中需要以数的大小为下标进行操作,但是数据太大,无法开这么大的数组,怎么办。若在题目当中,我们只需要用到数与数之间的相对大小关系,而不需要数的具体数值,则可以使用离散化。(例如:求逆序数的对数)
数据的离散化:离散化,把无限空间中有限的个体映射到有限的空间中去,以此提高算法的时空效率。(by百度百科)。即:不改变数与数之间的相对大小,使大的数尽量小。
例如上面的那个例子,数只有50000个,但是范围巨大,于是我们可以把50000个数用1-50000来表示:给数排个序,然后最大的数为50000,最小的为1(前提是我们只需要使用数的相对大小,而不用每个数的具体数值)。
可以先看例题:51nod1219:https://www.51nod.com/onlineJudge/questionCode.html#!problemId=1019
下面是离散化的代码(下为51nod1219的代码中离散化的操作):
1 //数据离散化 2 pair<int,int> p[MAXN]; //声明一个pair容器,用来存初始数据以及数据的初始下标 3 4 for(int i=1; i<=n; ++i) 5 { 6 scanf("%d",&p[i].first); //容器的第一个元素为数据大小 7 p[i].second = i; //容器的第二个元素为下标 8 } 9 10 int change[MAXN]; //声明一个数组用来存离散化之后每个数的相对值 11 sort(p+1,p+1+n); //按数据大小排序(容器pair自动按first排序) 12 for(int i=1; i<=n; ++i) //获得离散化之后的相对值 13 { 14 change[p[i].second] = i; 15 }
上面的代码怎么理解:用一个容器存下初始序列以及他们对应的下标,例如:
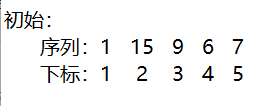
上图中,数据是无序的,下标是有序的,然后我们按数据排序后,变成了下图:

上图中:数据变成有序的了,而之前存下的下标变为了无序的,但却表示的是序列在未排序前的位置,而当前下标则表示的是数据之间的相对大小,也就是离散化后的相对值。
而上图可以理解为,未排序前:
序列中最小的1,在原序列中是在第1个位置,离散化的相对值即为1,代码中change[1] = 1;
序列中的第2小的6,在原序列中是在第4个位置,离散化的相对值为2,代码中的change[4] = 2;
序列中的第3小的值为7,在原序列中是在第5个位置,离散化的相对值为3,代码中的change[5] = 3;
序列中的第4小的值为9,在原序列中是在第3个位置,离散化的相对值为4,代码中的change[3] = 4;
序列中的最大值为15,在原序列中是在第二个位置,离散化的相对值为5,代码中的change[2] = 5;
离散化完成后,原序列变为了1 5 4 2 3;


