CCPC绵阳站

7-11 Knowledge is Power

Knowledge is power. Little Rabbit and Little Horse both long for more knowledge, so they always challenge each other to some quizzes. Today, Little Rabbit creates a new quiz for Little Horse.

Little Rabbit gives Little Horse a positive integer x. Little Horse needs to find a set of integers , that meets the following conditions.

• n≥2
• a​i​​>1, for 1
• ∑​i=1​n​​a​i​​=x
• a​i​​ and a​j​​ are co-prime, for any i≠j

For example, if 2, then 3 and 5 and 2 are all valid sets. Two integers are said to be co-prime if the only positive integer that evenly divides both of them is 1.

We define a​_max​​ as the maximum element of S, and a​_min​​ as the minimum element of S. Little Rabbit wants the value of (a​_max​​−a​_min​​) to be as small as possible. Can you help Little Horse to find the minimum value of (a​_max​​−a​_min​​) ?

Input

The first line of the input contains an integer T (1≤T≤10​5​​) − the number of test cases.

Each test case contains an integer x (5≤x≤10​9​​) − the integer Little Rabbit gives to Little Horse.

Output

For the x-th test case, if the answer is y, output Case #x: y in a single line. If there's no possible solution, output Case #x: -1 in a single line.

Sample Input

4
5
6
7
10

 

Sample Output

Case #1: 1
Case #2: -1
Case #3: 1
Case #4: 3

思路：
第一种思路就是打表找规律，打一百个数应该就可以看出来了。36个为一循环（实话讲我不太会写打表代码，但是队里有人这样做出来了！）

100个数中，36个数为一循环，可以直接写，代码就不附带了，毕竟我有更高级的方法。

首先，注意到6是没有分法的。
如果把6分成两个数，如下图所示，没有符合题意的分法。

 

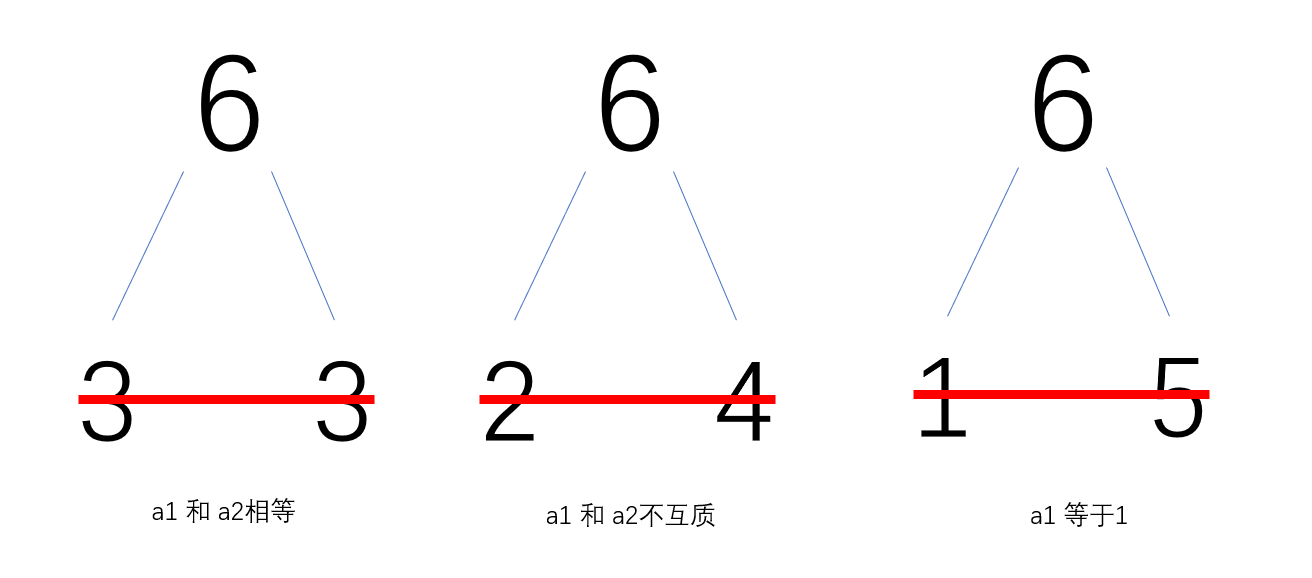
如果按照分成三个数的方法，显然也不会有符合题意的情况，所以特判6。

注意x的范围≥5，所以不用考虑5以下。

接着分类讨论，在x是奇数的情况下，显然最优的分法是分成 x / 2, x / 2 + 1。在这个条件下，(a​_max​​−a​_min​​)的值是1。

对于偶数，则分两种情况，首先如果分成两个数字，a₁和a₂不能相等，所以应该是把x拆成 x / 2 - 1, x / 2 + 1。

如果 x / 2 - 1 是奇数，显然他们互质。且这时候是最优解， 因为分成三个数的最优情况a₁和a₃的差是3，n个数以此类推，所以分成两个数是最优解。

如果 x / 2 - 1 是偶数，就不能按照这种拆分方式分。

　　此时有两种方案：

　　第一种，把x拆成 x / 2 - 2, x / 2 + 2; 此时(a​_max​​ − a​_min​​) = 4。

　　第二种，拆分成三个数。此时最优情况下(a​_max​​ − a​_min​​) = 2， 次优情况下(a​_max​​ − a​_min​​) = 3。

　　显然如果第二种成立优先选择第二种。

　　拆分成三个数最优情况是 奇， 偶， 奇。 如果x恰好是3的倍数，即可拆成 x / 3 - 1, x / 3, x / 3 + 1。(a​_max​​ − a​_min​​) = 2。

　　如果不是3的倍数又分两种情况，x = 3n + 1, x = 3n + 2。

　　

 

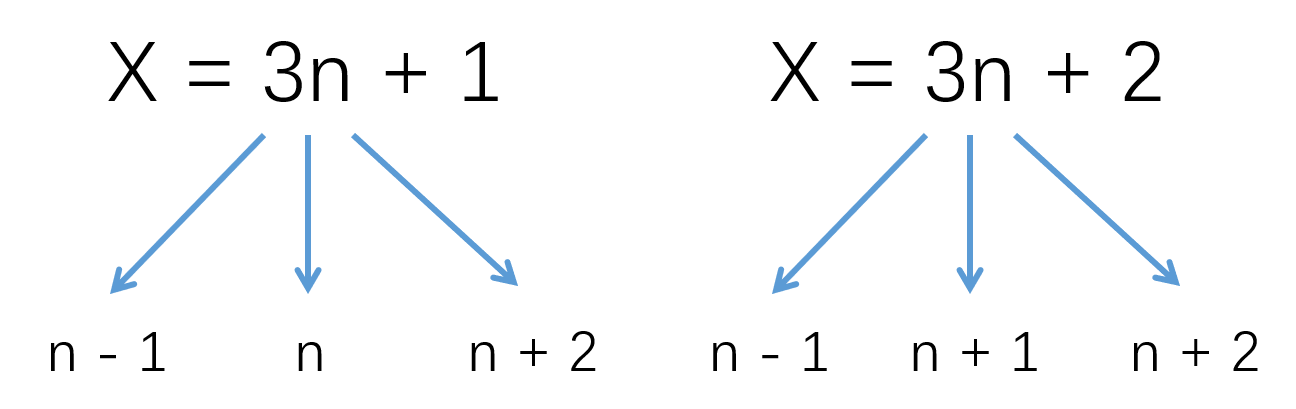
 　　然后我就在这里翻车了，没有考虑到 n - 1 和 n + 2 可能为3的倍数的情况，只要再加一个特判，判断 n - 1是否为3的倍数即可。

　　代码如下。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn = 1e6 +10;
 
int main()
{
    int t;
    cin >> t;
    for(int i = 1; i <= t; i++)
    {
        int x;
        cin >> x;
        if(x % 2) cout << "Case #" << i << ": 1" << endl;
        else if(x == 6) cout << "Case #" << i << ": -1" << endl;
        else
        {
            if(x % 4 == 0 || x % 3 == 0) cout << "Case #" << i << ": 2" << endl;
            else if(x % 3 == 1)
            {
                if(((x - 1) / 3 - 1) % 3 == 0) cout << "Case #" << i << ": 4" << endl;
                else cout << "Case #" << i << ": 3" << endl;
            }else
            {
                if(((x - 2) / 3 - 1) % 3 == 0) cout << "Case #" << i << ": 4" << endl;
                else cout << "Case #" << i << ": 3" << endl;
            }
        } 
    }
}