什么是极坐标？ —— 一点微小的想法 What is Polar Coordinate ? - Some Naive Thoughts about It

Can you answer these three questions? The answer seems to be trivial, since we can use our eyes to obtain the answer. But can you use mathematical methods to answer it correctly?

1. Find the intersection point(s) of \(r=2\theta\) (called the Archimedes spirals, or equation A) and \(\theta=\pi\) (equation B), in the polar coordinate system. (Given that \(r \geq 0\).) (Adapted from Thomas Calculus P675, Q88)
2. Suppose we have a polar equation \(r = 1 + \cos2\theta\)(equation A). Determine whether the following statement is true: When we plug in \((-r, \theta)\), the equation becomes \(-r = 1 + \cos2\theta\) (equation B), which is evidently not on the original curve. Therefore, the curve is not symmetric about the origin. (Adapted from Home Assignment 4, Q3(2))
3. Suppose a hyperbola is determined by the equation \(r=\frac{6}{1-2\cos\theta}\) (equation A). Calculate the intersection point(s) with the curve \(\theta = 0\) (equation B). If we try to find the common solution to the two equations, we will only get \((-6,0)\) but miss \((-2,0)\). So what is wrong with it? (Given that \(r \in \mathbb{R}\) and \(\theta \in \left[0, 2\pi\right]\), as is claimed to be default by the textbook.) (Adapted from lecture notes, week 4)

Firstly, let's think about a question which seems to be quite trivial: What are the intersection points of two curves? What are the common solutions of two polar equations? Are they the same, or, can I obtain the intersection if I know the common solutions? It seems quite trivial that the two are equivalent, as is taught since junior high school. However, if that is true, the answer in Q1 should be \((2\pi, \pi)\), and you can only get one common solution to Q3, which by intuition is wrong if you draw its curve. So what's wrong with it?

The main problem is that one point in a classical plane has multiple corresponding coordinates. For instance, in Q1, although \((6\pi, 3\pi) \in A\) and \((6\pi, \pi) \in B\) are exactly the same point in the classical plane, it is not the common solution to the two equations because the two are different coordinates. Generally speaking, common solutions to two equations can only determine those who have same coordinates. They will miss out those who are actually same points but have different coordinates.

To address this problem, please allow me to first define the so-called "stack planes", or SP. To avoid confusion, the "plane" that we usually talks about is called "classical plane" in this essay. As is shown in Fig.1, a SP consists of a stack of planes with the names of \(\ldots\), \(\#0^+\), \(\#0^-\), \(\#1^+\), \(\#1^-\), \(\ldots\) . In this notation, the \(\#k\) represents that all points in this plane must satisfy \(\theta \in \left[2k\pi, 2\left(k+1\right)\pi\right]\). The superscript denotes the range of \(r\). \(\#k^+\) requires \(r \geq 0\), and \(\#k^-\) requires \(r < 0\).

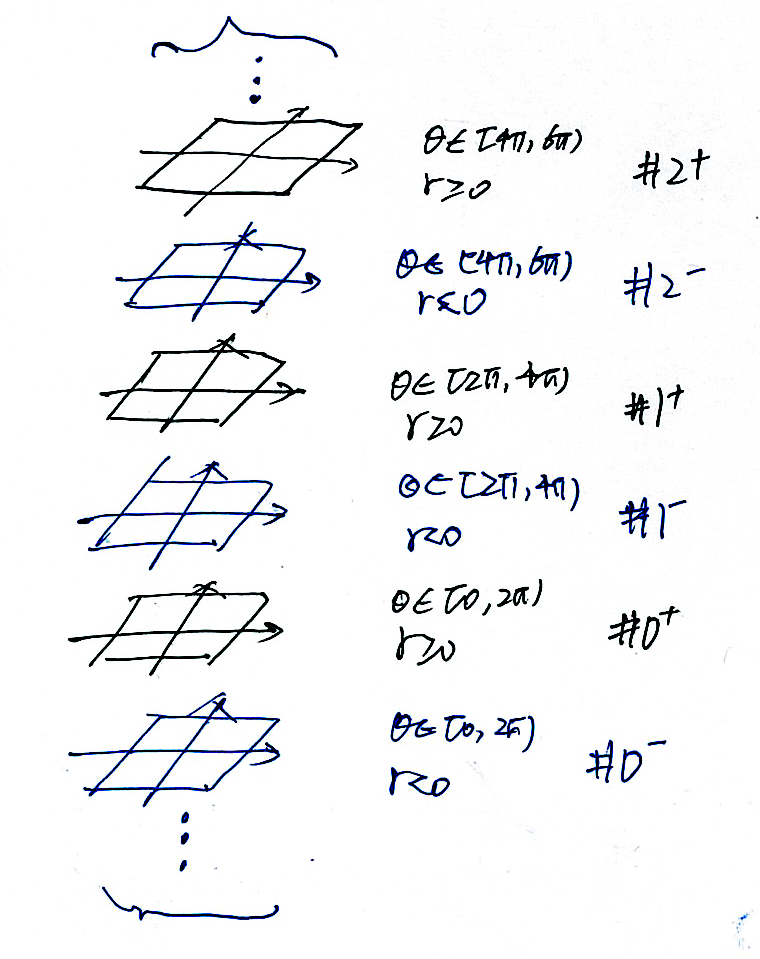
For instance, the plane \(\#0^+\) contains all points whose \(\theta \in \left[0,2\pi\right]\) and \(r \geq 0\), and the plane \(\#0^-\) contains those satisfying \(\theta \in \left[0,2\pi\right]\) and \(r < 0\).
If we there is no constrain on \(r\) and \(\theta\), there will be infinitely many planes in SP. If we constrain \(r \in \mathbb{R} \ and \ \theta \in \left[0,2\pi\right)\), there will be only 2 planes, \(\#0^+\) and \(\#0^-\), in the SP. Similarly, if we constrain \(r \geq 0\) and \(\theta \geq 0\), only the \(\#0^+, \#1^+, \ldots\) will be in the SP.

It can be seen that every point in SP has a one-to-one mapping to the polar coordinate. Therefore, there is no trouble about multiple-to-one correspondence in a normal plane. For example, the point in \(\#1^+\) plane which is one unit top from the origin is uniquely associated with coordinate \((1, \frac{5}{2}\pi)\).
We can further apply it to equations easily. That is, every solution in a polar equation has a one-to-one mapping with a point in SP. Take \(r = 2\theta\) in Q1 as an example. As is shown in Fig. 2, the corresponding graph in SP spreads through \(\#0^+, \#1^+, \ldots\), each of which has a part of the curve.

Therefore, the meaning of the common solutions of two equations is clear. It is not the intersection of two corresponding curves in the classical plane, due to the multiple-to-one mapping. Instead, it is the intersection of two curves in SP, since they have a one-to-one correspondence.

What is the relationship between SP and a classical plane? Or, what is the curve in a classical plane given a curve in SP? The answer is that the classical plane is the superposition of all the planes in a SP. Intuitively, you just "squeeze", "flatten" or "project" all the planes in a SP down, and the result is the classical plane. Take Q3 as an example. As is shown in Fig. 3, the bottom one is the classical plane, while the above two make up SP, and you can see the meaning of "projection" clearly.

How can we get the intersection in a classical plane, if we cannot do it by directly calculating the common solutions of two equations?
Recall that the common solutions of two equations only have the one-to-one correspondence with the intersections in SP, not intersection in classical planes. Therefore, the methodology is to transform the equation, such that all the intersections in classical planes are also intersections in SP. At the same time, the corresponding curve in the classical plane should not be changed. There are mainly two approaches to achieve that goal.

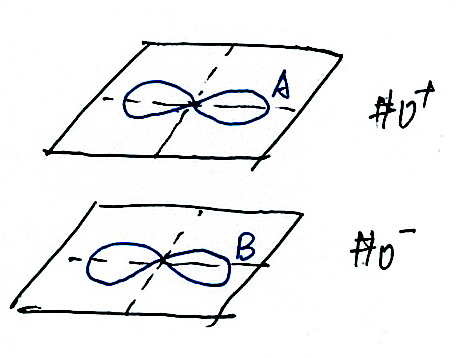
Firstly, we can transform the equations, such that the corresponding points are all in one single plane of SP, typically \(\#0^+\). It can be intuitively called "squeeze". For instance, in Q2, equation \(A\) and \(B\) do have no common solutions. But that is because curve \(A\) is in plane \(\#0^+\) while curve \(B\) is in plane \(\#0^-\), which is shown in Fig. 4. Therefore, we should transform the equation \(B\) to plane \(\#0^+\) by means of \((r, \theta) \to (-r, \theta + \pi)\). Then \(B\) becomes \(B'\), or \(-(-r) = 1 + \cos(2(\theta+\pi))\), i.e. \(r = 1 + \cos(2\theta)\). Therefore, it is clear that \(B'\) is essentially the same as \(A\), so the curve is symmetric about the origin.

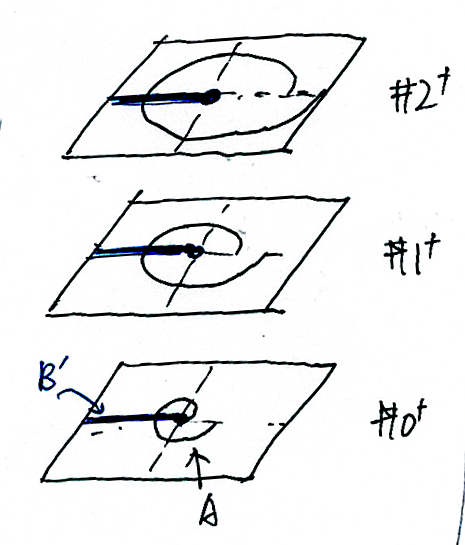
Secondly, we can transform the equations such that there is one duplicate in every plane. Therefore, there is no chance for them to "miss" each other. It can be called "expand". For example, to solve Q1, we can expand curve \(B\) to all planes of SP which curve \(A\) lies in. To achieve this, we transform \(B\) into \(B'\), which is defined by the union of \(\theta=\pi\) and \(\theta=3\pi\) and \(\theta=5\pi\) and \(\ldots\) . As is shown in Fig. 5, now the curve \(B'\) not only stay in plane \(\#0^+\) as \(B\) does, but is in all planes that \(A\) is in. Then we can find the common solutions of \(A\) and \(B'\), which is \((2\pi, \pi)\), \((6\pi, 3\pi)\), \(\ldots\), or equivalently, \(((4k-2)\pi, \pi)\) where \(k \in \mathbb{N}\).

How to plot a curve in SP? It is quite similar to what you have done when you want to plot a curve in the polar plane or Cartesian plane. You just need to traverse the \(\theta\), find out the \(r\), and plot them into lines. The only difference is that you need to plot into corresponding planes in SP, instead of putting all into one classical plane.

With all the discussion above, now we can come to the solutions to the questions above. Q1 and Q2 have been solved during the discussion, and here is the solution to Q3:
We first plot the two curves in SP, which is shown in Fig. 6. Then we can clearly see that the two curves in SP have only one intersection, the point \(P\), but miss out point \(Q\). That is the reason why we miss one point. In order to prevent this, we can use the "expand" method and change equation \(B\) to \(\theta = 0\) and \(\theta = \pi\). Therefore, all two solutions can be calculated.

The aforementioned ideas are just my naive thoughts, but it really solved what had troubled me since my high school, and I hope that it can be of some help to you! 😃

Tom Chen

2018.02.07