20182310第十周学习总结
20182310 2019-2020-1 《数据结构与面向对象程序设计》第十周学习总结
教材学习内容总结
本周主要学习无向图、有向图、带权图、常用的图算法、图的实现策略。
-
1.与树类似,图由结点和这些结点之间的连接构成。
顶点(vertice)就是这些结点。
边(edge)就是这些结点连接起来的线段。
路径(path):图中的一系列边,每条边连通两个顶点。
路径的长度(length):是该路径中边的条数(或者是顶点数减去1)。
环路(cycle):一种首结点和末结点相同且没有重边的路径。没有环路的图称为无环的(acyclic)。
完全图(complete graph):含有最多条边的无向图
对有n个结点的无向图,要使该图是完全的,要求有n(n-1)/ 2个边。
对有n个结点的有向图,要使该图是完全的,要求有n(n-1)个边。
![]()
-
2.无向图是一种边为无序结点对的图。
无序结点(undirected vertice):A、B、C、D
边(edge)(注:由于无序,所以<a,b>和<b,a>一样):(A,B) (B,D) (A,D) (B,C) (C,D)
邻接(adjacent):如果图中两个顶点之间有一条连通边,则称这两个顶点是邻接的。如图,A和B邻接,A和C不邻接。
自循环(self-loop)或环(sling):连通一个顶点及其自身的边称为自循环,如图,边(A,A)表示是A连接自身的一个环。
连通(connected):如果无向图中的任意两个顶点之间都存在一条路径,则认为这个无向图连通。 -
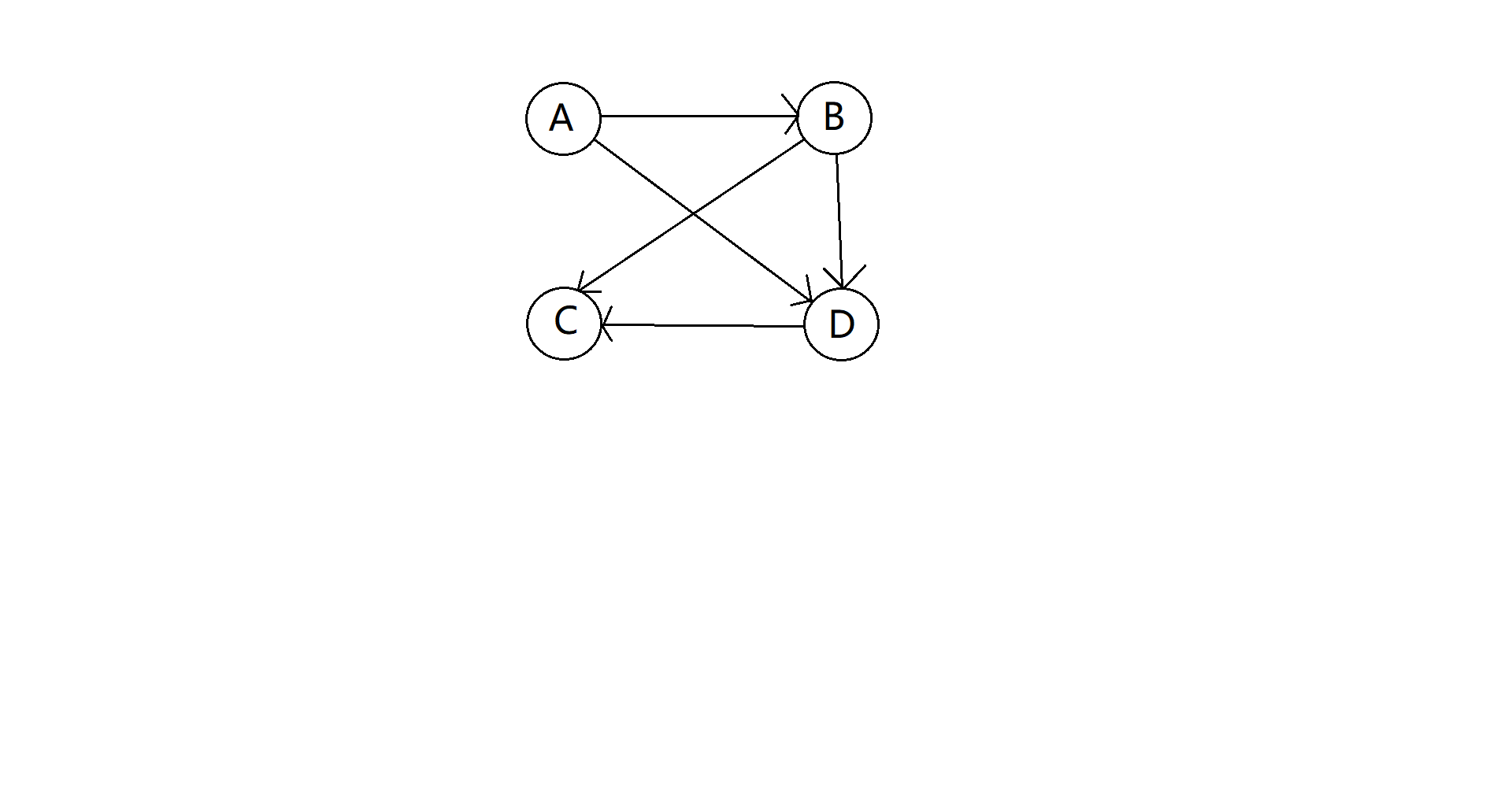
3.有向图
边为有序顶点对的图。也称为双向图(digraph)。
有序结点(directed vertice):A、B、C、D
边(edge)(注:由于有序,所以<a,b>和<b,a>不同):(A,B) (B,D) (A,D) (B,C) (D,C)
连通(connected):如果有向图中的任意两个顶点之间都存在一条路径且能通过一些路径遍历到所有的顶点,则认为这个有向图连通。
![]()
-
4.常见的图算法:
-
遍历
广度优先遍历:类似树中的层次遍历。把图的每一邻接的横向依次遍历。
深度优先遍历:顾名思义,把图的每一邻接的纵向遍历,类似树的前序遍历。
深度优先遍历和广度优先遍历的唯一不同是使用的是栈而不是队列来管理。 -
测试连通性:
从任意结点开始的广度优先遍历中得到的顶点数等于图中所含顶点数,则是连通的。 -
最小生成树(minimum spanning tree):边的权值之和小于或等于其他任意一棵生成树的边的权值之和。
-
图的实现策略:用邻接列表或者邻接矩阵等。有向图和无向图是不同的。
-
5.邻接列表:用一种类似于链表的动态结点来存储每个结点带有的边。这种链表称为邻接列表。
邻接矩阵:用一种叫邻接矩阵的二维数组来表示任意两个顶点的交接情况。
无向图的邻接矩阵一定是对称的,有向图的邻接矩阵不一定对称。
教材学习中的问题和解决过程
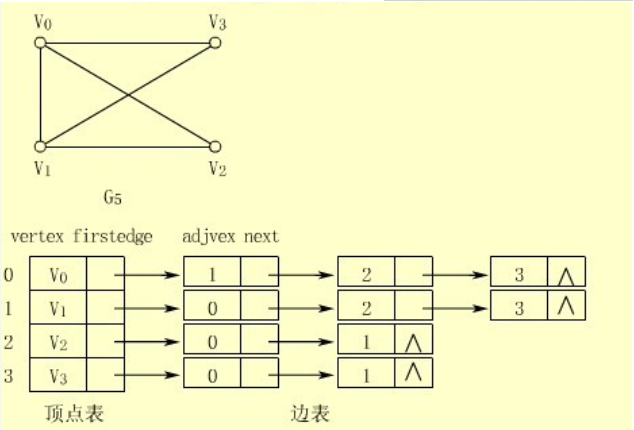
- 问题1:邻接表的处理方法?
- 问题1解决方案:
![]()
![]()
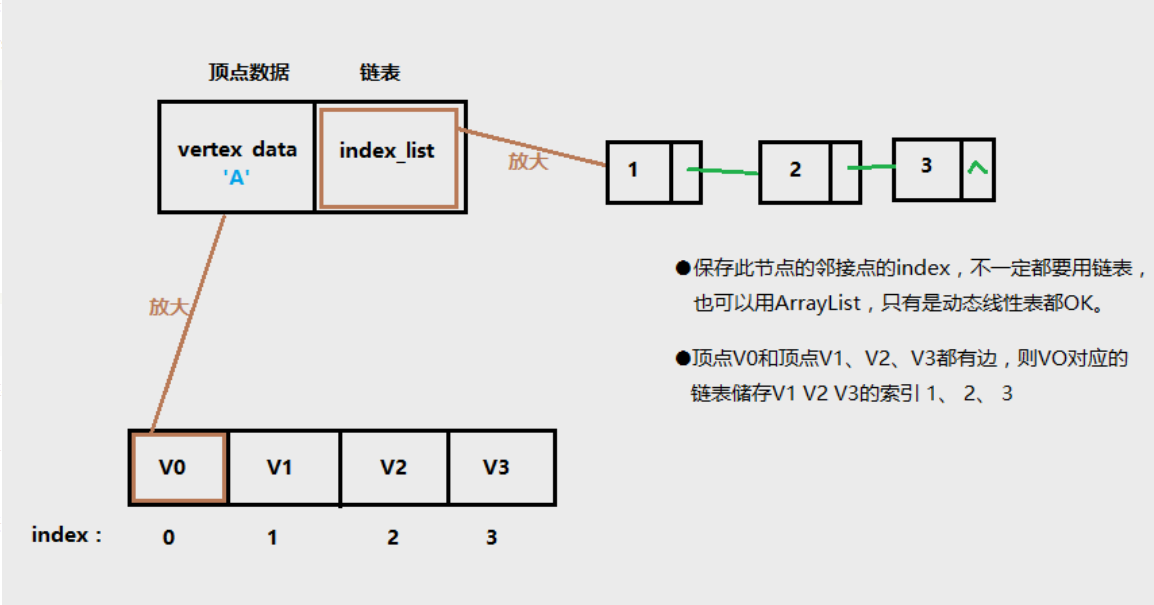
1、图中顶点用一个一维数组存储,另外,对于顶点数组中,每个数据元素还需要存储指向第一个邻接点的指针,以便于查找该顶点的边信息。
2、图中每个顶点vi的所有邻接点构成一个线性表,由于邻接点的个数不定,所以用单链表存储,无向图称为顶点vi的边表,有向图称为顶点vi作为弧尾的出边表。
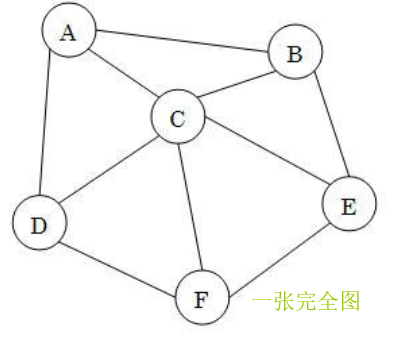
- 问题2:关于选课问题,即四色问题的一点疑惑
- 问题2解决方案:这个问题在我当时学离散的时候就没有完全理解,四色定理是一个著名的数学定理,通俗的说法是:每个平面地图都可以只用四种颜色来染色,而且没有两个邻接的区域颜色相同。四色定理的本质就是在平面或者球面无法构造五个或者五个以上两两相连的区域。这一定理最初是由Francis Guthrie在1853年提出的猜想。1976年借助电子计算机证明了四色问题,问题也终于成为定理,这是第一个借助计算机证明的定理。
四色定理 指出每个可以画出来的地图都可以至多用4种 颜色 来上色,而且没有两个相接的区域会是相同的颜色。被称为 相接 的两个区域是指他们共有一段边界,而不是一个点。
这一定理最初是由Francis Guthrie在1853年提出的猜想。很明显,3种颜色不会满足条件,而且也不难证明5种颜色满足条件且绰绰有余。但是,直到1977年四色猜想才最终由Kenneth Appel 和Wolfgang Haken证明。他们得到了J. Koch在算法工作上的支持。
证明方法将地图上的无限种可能情况减少为1 936种状态(稍后减少为1 476种),这些状态由计算机一个挨一个的进行检查。这一工作由不同的程序和计算机独立的进行了复检。在1996年,Neil Robertson、Daniel Sanders、Paul Seymour和Robin Thomas使用了一种类似的证明方法,检查了633种特殊的情况。
代码调试中的问题和解决过程
-
问题1:在写有向图和无向图的代码时,图中删除结点操作,能否调用删除边的操作。
-
问题1解决方案:我认为 ,删除结点,就是把结点与其他结点的边删除,然后结点个数减1。
但是这样是有缺陷的。删除结点后,结点消失;但是删除边,边消失,节点依然存在,因此没有起到相同的效果。 -
问题2:测试连通性,通过比较广度优先遍历中的顶点数目和图中的顶点数目是否相等来判断,即任意一个顶点都必须满足这个条件。那么为什么不只要判断出有广度优先遍历的顶点数目和图中的顶点数目不相等的时候就不连通呢,这样可以有效减少遍历次数,优化算法的效率。
-
问题2解决方案:在IDEA上利用课堂实践的有向图和无向图的代码进行设想后发现,结果是:
在有向图中,路径是不可逆的,也就是说,顶点存在有可能正向出发遍历所有的顶点,而反向却不可以。 这时,为了保证任意顶点广度优先遍历的顶点数目和图中的顶点数目相等,我们需要从所有顶点遍历一次。
但是对于无向图来说,是可行的,并且提高了效率。
代码托管
上周考试错题总结
上周没有进行考试,所以没有错题。
结对及互评
评分标准
- 博客中值得学习的或问题:
- 学习:在总结问题时有附上详细的图片,而我总是忘记截图,代码中出现的问题也能及时自己发现错误来源。
- 问题:教材学习内容总结不够详细。
- 代码中值得学习的或问题:无
- 基于评分标准,我给本博客打分:15分。得分情况如下:
-
正确使用Markdown语法(加1分):
-
模板中的要素齐全(加1分)
-
教材学习中的问题和解决过程, 一个问题加1分()
-
代码调试中的问题和解决过程, 一个问题加1分()
-
本周有效代码超过300分行的(加2分)
-
其他加分:
- 感想,体会不假大空的加1分
- 排版精美的加一分
- 进度条中记录学习时间与改进情况的加1分
- 有动手写新代码的加1分
- 课后选择题有验证的加1分
- 错题学习深入的加1分
- 点评认真,能指出博客和代码中的问题的加1分
- 结对学习情况真实可信的加1分
点评过的同学博客和代码
其他(感悟、思考等,可选)
图这一章不太好学,课堂实践也很多,很多算法实现都没见过,需要好好理解消化。有些逻辑也较为复杂,需要潜心判断和思考。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 10000行 | 30篇 | 400小时 | |
| 第一周 | 155/200 | 2/2 | 20/20 | 初步掌握linux命令、java小程序和jdb调试 |
| 第二 三周 | 470/625 | 2/4 | 20/40 | 学会scanner定义的使用,类的定义 |
| 第四周 | 1444/2069 | 2/4 | 20/60 | 下载安装IDEA及其插件,学会TDD调试,编写测试代码 |
| 第五周 | 1917/3986 | 2/8 | 20/80 | 简单的学会客户端和服务器的编写 |
| 第六周 | 1324/5310 | 1/9 | 20/100 | Java封装,继承,多态 |
| 第七周 | 2795/8105 | 3/12 | 40/140 | 栈,链表 |
| 第八周 | 1135/9240 | 1/13 | 40/180 | 选择,排序 |
| 第九周 | 2039/10131 | 3/16 | 40/220 | 二叉树,堆排序 |
| 第十周 | 1590/11721 | 2/18 | 40/260 | 图的遍历,图的简单算法 |




 浙公网安备 33010602011771号
浙公网安备 33010602011771号