20182310第九周学习总结
《数据结构与面向对象程序设计》第九周学习总结
教材学习内容总结
- 树的概述:
树由一个包含结点和边的集构成。 树中结点和边的关系是:总边数 = 总结点数 - 1。
根结点:就是指位于该树顶层的唯一结点。一棵树只有一个根结点,根结点没有父节点。
子结点:一个树中较低层的结点是上一层结点的子结点。也叫作其孩子。
兄弟结点:同一双亲的两个结点。
叶结点:没有任何子结点的结点。
内部节点:一个至少有一个子结点的非根节点。
路径长度:通过计算从根到该结点所必须越过的边数目。
高度:从根到叶子之间的最远路径的长度。
度:树中任一结点可以具有的最大孩子的数目。
含有m个元素的平衡n元树具有的高度为lognm。 - 树的分类:
二叉树:结点最多具有两个孩子的树。
广义树:对结点所含有的孩子数目没有限制的树。
平衡树:粗略的来说,如果树的叶子都位于同一层或者至少彼此相差不超过一层,那么就称之为平衡的。
完全树:如果某树是平衡的,且底层所有叶子都位于树的左边,则认为该树是完全的。 完全二叉树在每个k层上都有2^k个结点,最后一层除外,在最后一层的结点必须是最左边的结点。
满树:如果一颗n元树的所有叶子都位于同一层且每一结点要么是一片叶子,要么是正好具有n个孩子。 满树一定是完全树。 - 树的遍历

前序遍历:从根结点开始,访问每一个结点及其孩子。(A->B->D->E->C)
Visit node
Traverse(left child)
Traverse(right child)
中序遍历:从根结点开始,访问结点的左侧孩子,然后是该结点,再然后是任何剩余的结点。(D->B->E->A->C)
Traverse(left child)
Visit node
Traverse(right child)
后序遍历:从根结点开始,访问结点的孩子,然后是该结点。(D->E->B->C->A)
Traverse(left child)
Traverse(right child)
Visit node
层序遍历:从根节点开始,访问每一层的所有结点,一次一层。(A->B->C->D->E)
-
二叉查找树(binary search tree):二叉树定义的扩展,一种带有附加属性的二叉树。附加属性是什么?树中的每个节点,其左孩子都要小于其父节点,而父节点又小于或等于其右孩子。
-
堆排序
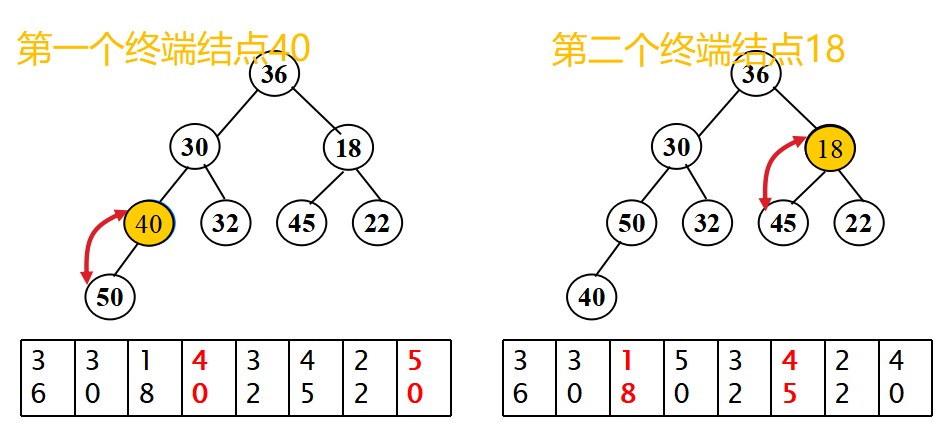
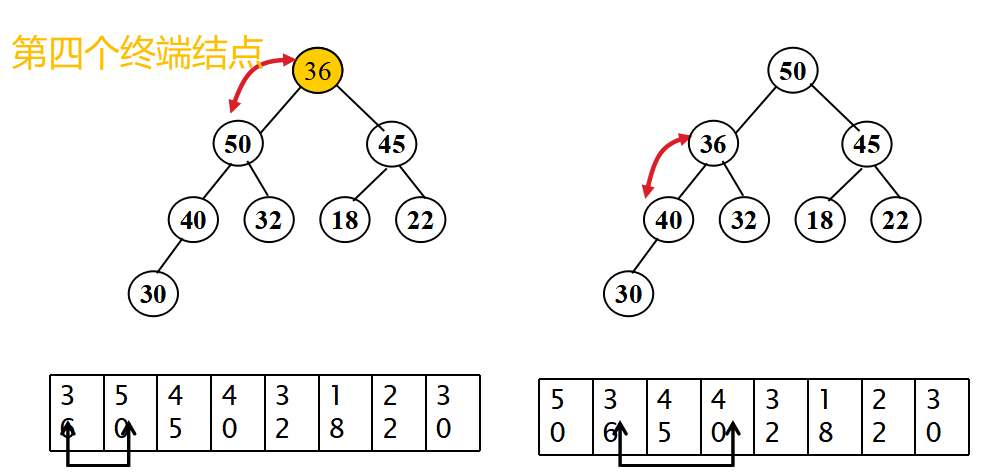
-
3.关于堆排序的内容:
原理:根据堆的有序属性,将列表的每一个元素添加到堆中,然后一次一个的把他们从根中删除。
堆排序是一种选择排序,整体主要由构建初始堆+交换堆顶元素和末尾元素并重建堆两部分组成。其中构建初始堆经推导复杂度为O(n),在交换并重建堆的过程中,需交换n-1次,而重建堆的过程中,根据完全二叉树的性质,[log2(n-1),log2(n-2)...1]逐步递减,近似为nlogn。所以堆排序时间复杂度一般认为就是O(nlogn)。
堆排序时间复杂度O(nlogn)。
步骤:
步骤一:构造初始堆。将给定无序序列构造成一个堆(升序采用小顶堆,降序采用大顶堆)。
步骤二:将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。 -
4.删除元素(removeElement):
在二叉查找树中删除一个给定的结点p有三种情况:
(1)结点p无左右子树,则直接删除该结点
(2)结点p有左子树(右子树),则把p的左子树(右子树)接到p的父节点上
(3)左右子树同时存在,找到结点p的中序直接后继结点s,把结点s的数据转移到结点p,然后删除结点s,由于结点s为p的右子树总最左的结点,因而s无左子树,删除结点s.
关于二叉树的基本操作方法:
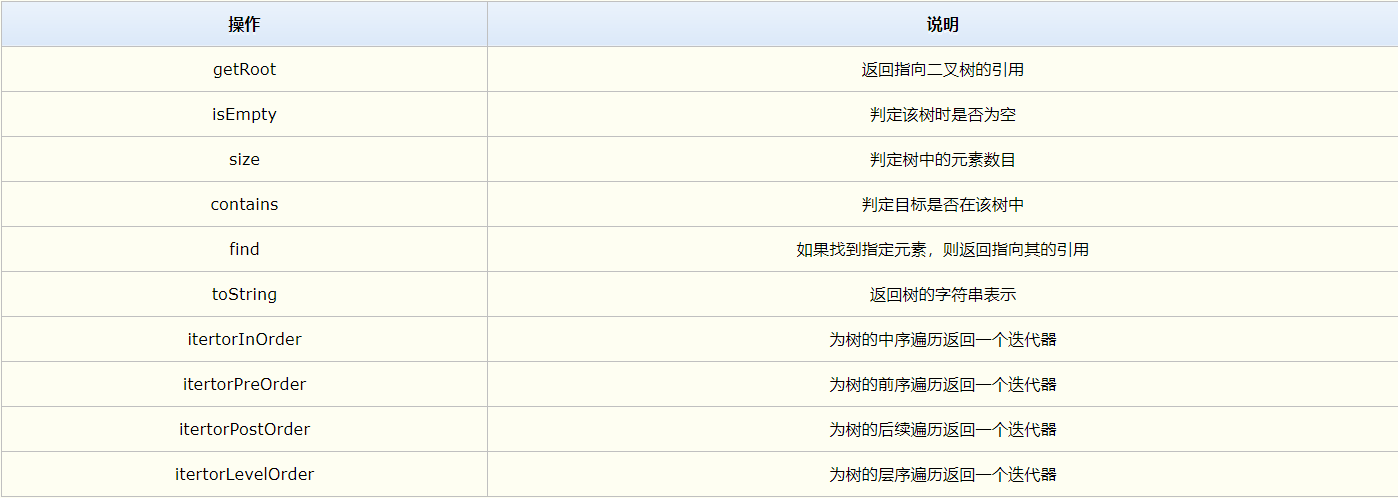
教材学习中的问题和解决过程
-
问题1:关于树,高度和深度究竟有什么区别?
-
问题1解决方案:高度和深度一组相反的概念
高度是指当前结点到叶子结点的最长路径,如所有叶子结点的高度都为0。
深度则是指从根结点到当前结点的最大路径长度,如根结点的深度为0。
高度就是从要计算的结点开始寻找最远路径长度,深度就是从根结点到该结点的最大路径长度;在一棵树中,高度+深度 = 树中最远的路径长度。 -
问题2:关于用链表实现堆,在敲完书本代码BinaryTreeNode后,还是有很多不了解的地方
-
问题2解决方案:因为要求插入元素以后能够向上遍历,所以堆中的结点必须存储指向双亲的指针。继承BinaryTreeNode类,并且添加双亲指针和对应的set方法。
关于add element操作
addElement操作:
在适当位置添加一个元素。
对堆进行重排序,以保持其有序属性。 -
问题3:关于代码中的root.getleft()出现异常的问题
-
问题3解决方法:查阅书籍后发现,只需要添加 LinkedBinaryTree left,right
然后在LinkedBinaryTree类的构造方法里加入this.left=left,this.right=right即可。
代码调试中的问题和解决过程
-
问题1:代码中未能实现树形输出,在本应该出现树形图案的地方出现如下情况:

-
问题1解决方案:在上网查阅资料,查询博客之后发现问题,修改toString方法,输出树状图案。
-
问题2:关于代码中的 height(BinaryTreeNode
node)方法中的递归是如何实现。因为if条件是node == null,那么到最后是不是返回的值是0?(即如下所示的代码)
// 返回这棵树的高度。
public int getHeight()
{
return height(root);
}
// 返回指定节点的高度。
private int height(BinaryTreeNode<T> node)
{
int left;
int right;
if (node == null)
{
return 0;
}
else
{
left = height(node.getLeft());
right = height(node.getRight());
if (left < right)
return right + 1;
else
return left + 1;
}
}
- 问题2解决方法:从根节点开始调用递归,然后一直找左子树,直到左子树为null。
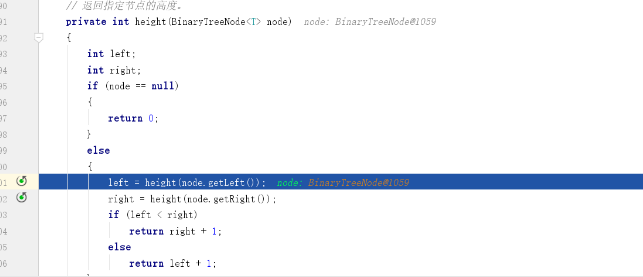
当这里left已经转为null了,那么下一个判断它将返回0。
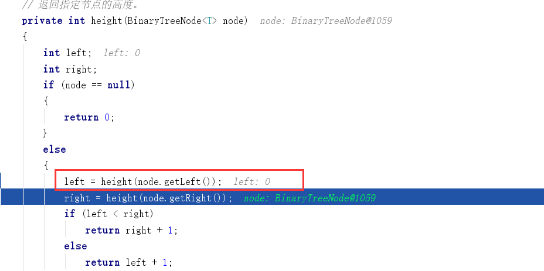
接着运行后发现left为0,这时候开始递归right。
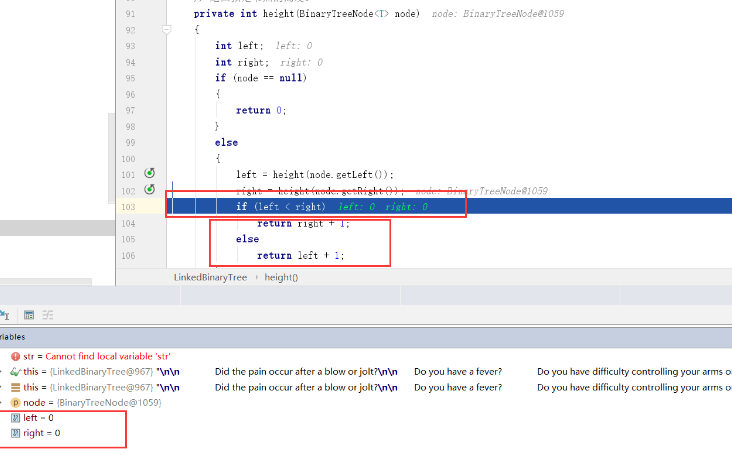
一直到左右都为0的时候,也就是没有左右孩子的时候,这时候的返回值是right + 1,所以不存在高度输出为0的结果
代码托管
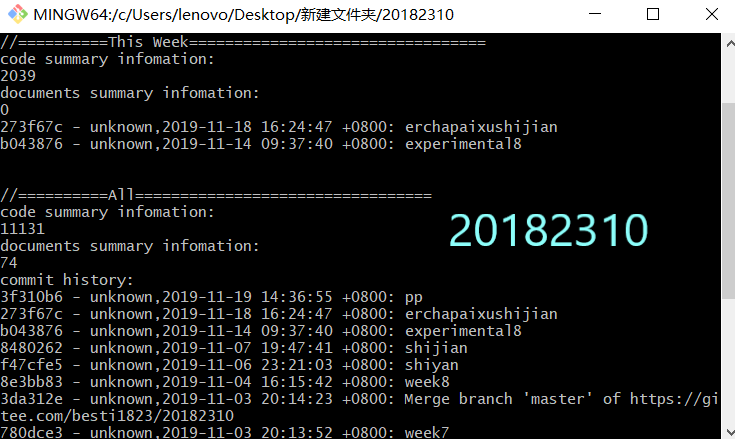
上周考试错题总结
上周没有进行考试,所以没有错题。
结对及互评
评分标准
- 博客中值得学习的或问题:
- 学习:在总结问题时有附上详细的图片,而我总是忘记截图,代码中出现的问题也能及时自己发现错误来源。
- 问题:教材学习内容总结不够详细。
- 代码中值得学习的或问题:无
- 基于评分标准,我给本博客打分:15分。得分情况如下:
- 正确使用Markdown语法(加1分):
- 模板中的要素齐全(加1分)
- 教材学习中的问题和解决过程, 一个问题加1分
- 代码调试中的问题和解决过程, 一个问题加1分
- 本周有效代码超过300分行的(加2分)
- 其他加分:
- 感想,体会不假大空的加1分
- 排版精美的加一分
- 进度条中记录学习时间与改进情况的加1分
- 有动手写新代码的加1分
- 课后选择题有验证的加1分
- 错题学习深入的加1分
- 点评认真,能指出博客和代码中的问题的加1分
- 结对学习情况真实可信的加1分
点评过的同学博客和代码
其他(感悟、思考等,可选)
最近学习的都是数据结构的知识,代码很复杂,不再是单单的一个类几个方法。相对应的代码量也变得多了起来,作业和课堂实践也变多了。但是博客还是应该要认真完成,不忘初心,继续努力!
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 10000行 | 30篇 | 400小时 | |
| 第一周 | 155/200 | 2/2 | 20/20 | 初步掌握linux命令、java小程序和jdb调试 |
| 第二 三周 | 470/625 | 2/4 | 20/40 | 学会scanner定义的使用,类的定义 |
| 第四周 | 1444/2069 | 2/4 | 20/60 | 下载安装IDEA及其插件,学会TDD调试,编写测试代码 |
| 第五周 | 1917/3986 | 2/8 | 20/80 | 简单的学会客户端和服务器的编写 |
| 第六周 | 1324/5310 | 1/9 | 20/100 | Java封装,继承,多态 |
| 第七周 | 2795/8105 | 3/12 | 40/140 | 栈,链表 |
| 第八周 | 1135/9240 | 2/14 | 40/180 | 选择,排序 |
| 第九周 | 2039/11131 | 3/17 | 40/220 | 树,二叉树,堆排序 |



