牛顿迭代法求根

三次方根

（cube.pas/c/cpp）

【问题描述】

自从在第2题中老师们的工作积极性提高以来，以Fengzee为首的学生们苦不堪言，因为老师给他们留了太多的作业，有些作业甚至是几乎无法完成的。这次，数学老师布置下了10道开三次方的作业题，要求同学们笔算完成。Fengzee当然不会花时间做这种没用的工作，他又没有计算器。这样的工作应当由电脑来完成，这就需要你编程序来解决。

    你的输入文件中只含有一个实数n，是待开三次方的数字。你的任务是计算这个数的三次方根，并输出在标准输出文件中。我们有算法设计限制条件：这道题的主要运算过程，你必须自己在程序中设计，且评测时使用的编译器已经去掉头文件math.h，就是说，你不能使用这个头文件中提供的一切函数。你只需要在文件中写入结果，不要加任何额外的文字。在满足算法设计限制条件的前提下，你的答案只需与标准答案相差不超过0.001，你即可得到全部的分数；而且你输出的数字的小数位数不受限制(小数点保留六位)。

【输入文件】输入文件cube.in

输入文件中只含有一个实数n，是待开三次方的数字。

【输出文件】输出文件cube.out

数n的三次方根。

【样例输入】

9

【样例输出】

2.08008  

【数据规模】

-10000<=n<=10000  

  一般实现

二分逼近法  （同学友爱的代码~）

#include <cstdio>
#include <iostream>
#include <algorithm>
#define eps 1e-8

using namespace std;

double n;

double fun(double mid)
{return mid*mid*mid<n?1:0;}

int main()
{
    cin>>n;
    double l=0,r=n,mid;
    if(n<0) swap(l,r);
    while(r-l>eps){              //当精度未达到1e-8即10-8时，二分逼近
        mid=(l+r)/2;
        if(fun(mid)) l=mid;     //小的话 
        else r=mid;
    }
    printf("%.6f\n",r);
}

然而我并没有想到这一点

反而想起牛顿老人家了

我要在巨人的肩膀上干事！！（其实是我蠢 =6=..）

没错 牛顿迭代法

定义 一种在实数域和复数域上近似求解方程的方法  --摘自百度

原理  不断用(x,f(x))的切线来逼近方程的根

递推公式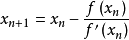  （证明过程可详见百度）

加深理解可以参考 如何通俗易懂的讲解牛顿迭代法

有了这个我们可以干什么呢。

当然是去解方程啦

求解步骤：
1. 原函数： f(x)=x^m-af(x)=xm−a
2. 原函数的导函数： f^'(x)=mx^m-1f′(x)=mxm−1
3. 使用牛顿迭代公式 

可得xn+1=xn−f(xn)f′(xn)=xn−xmn−amxm−1n

对于本题而言 可以看成解方程 x^3=a

代入公式可得 x_n+1=x_n-(x³-a)/3x_n²

如此自定义一个函数就好了

注意：牛顿法只能逼近解，不能计算精确解。不过实际应用中，我们都不要求绝对精确的解，只要精度足够高就好了  （所以此题我 wrong 了。）

#include <iostream>
#include <cstdio>
using namespace std;

int mabs(int a)
{
    if(a<0) a=-a;
    return a;
}
double sqrt(double c) 
{ 
   double err = 1e-8; //设立精度
   double t = c; 
   while (mabs(c - t*t*t) > err)  t =t-(t*t*t-c)/(3.000*t*t); //三次方的递推公式
   return t; 
}
int main()
{
        int n;
        cin>>n;
    printf("%.6lf",sqrt(n));
    return 0;
}

 输入值 9 输出值2.099878 误差有点大。

不过可以通过调参数来调整

同样的利用牛顿迭代法可以推导到一般情况，大家可以尝试一下。