常用算法(Java表述)
冒泡排序(Bubble Sort)
时间复杂度 O(n2),里层循环每趟比较第 j 项和第 j+1项,如果前项大于后项,则发生交换。缺点是每次比较后都可能发生交换,交换次数太多了,值从小到大。

通俗概述:依次比较相邻两关键字,如果反序则立即发生交换,如果正序则继续比较下一个相邻项,双重嵌套循环实现
参考代码:
package edu.tyut; import java.util.Arrays; /** * 冒泡排序:利用双重循环,如果前一个数比后一个数大,则发生交换,每次比较都发生交换 优化版:添加flag标记,循环外定义flag标记为true,进入循环后flag设为false,
若一次循环后发生了交换则将flag设为ture,进入下次循环;若整次循环只发生比较未发生交换,则说明数组已经有序,后续循环比较则不必要了,减少比较次数,提升性能 */ public class BubbleSort { public static void bubbleSort(int[] arrs) { int temp = 0; boolean flag=true;//用flag作标记,当没有发生交换的时候,说明数组已经是有序的了。 for (int i = 0; i < arrs.length - 1&&flag; i++) { flag=false;//flag标记初始化为false; for (int j = 0; j < arrs.length - i - 1; j++) { //判断当前项是否大于后一项 if (arrs[j] > arrs[j + 1]) {//是,则发生交换 temp = arrs[j]; arrs[j] = arrs[j + 1]; arrs[j + 1] = temp; flag=true;//发生交换flag标记设为true } } } } public static void main(String[] args) { int[] arr=new int[]{2,6,5,4,2,4,6,9,7}; System.out.println(Arrays.toString(arr)); bubbleSort(arr); System.out.println(Arrays.toString(arr)); } }
简单选择排序(Simple Selection Sort)
简单选择排序:就是通过n-1次关键字间的比较,从n-i+1个记录中选出关键字最小的记录,并和i(1<=i<=n)个记录交换值
时间复杂度 O(n2),在冒泡排序的基础上,只不过每次比较后,将保存最小值的索引指向小值,在一次循环结束时,将最小值与循环首项发生交换。整体分为已排序和未排序两部分,值从小到大。
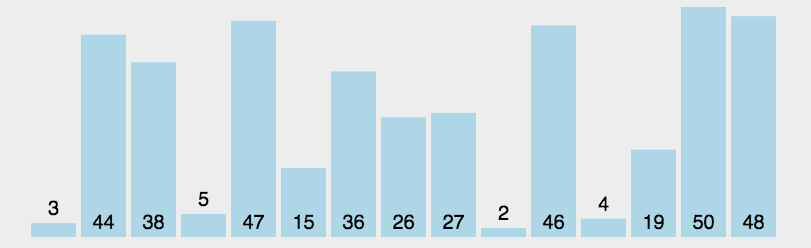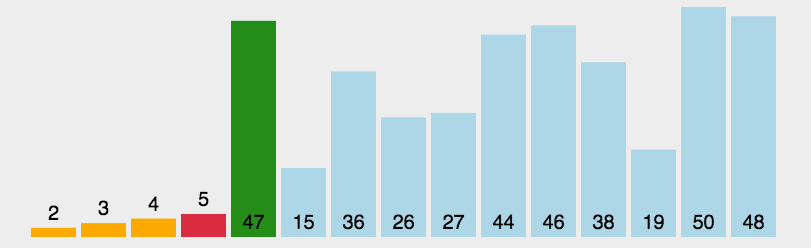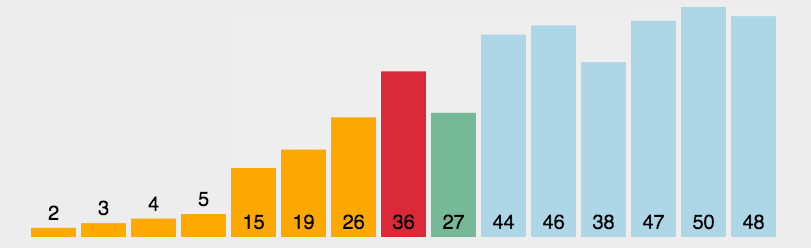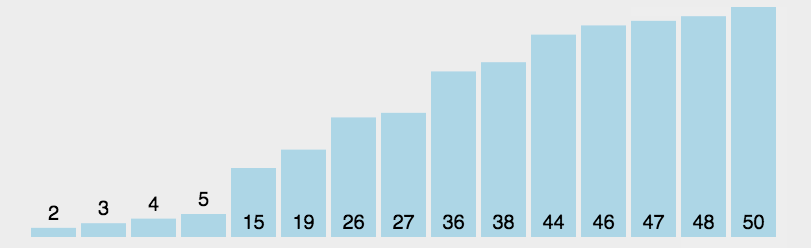
注意区别:冒泡排序跟直接选择排序都是依次比较相邻的记录,但是冒泡排序是一有反序立即交换,而直接插入排序则是出现反序将最小值记录下来,最后再发生交换。
参考代码:
package edu.tyut; import java.util.Arrays; /** * 简单选择排序:在待排序中找出最小值,然后放到已排序的末尾 * 利用双重for循环,找出最小值,再发生一次交换 */ public class SelectionSort { //需要遍历获得最小值的次数 //要注意一点,当要排序N个数,已经经过N-1次遍历后,已经是有序数列 public static void selectSort(int[] arrs) { for (int i = 0; i < arrs.length - 1; i++) { int temp=0; int index=i;//用来保存最小的索引,初始指向当前第i项 //从未排序数中找出最小值,这里最大索引应该是数组最后一位即length-1 for (int j = i+1; j <arrs.length; j++) { //如果后面的值比索引值还小,则将索引指向最小值 if (arrs[j]<arrs[index]){ index=j; } } //已经找到最小值,然后将最小值放到已排序的末尾 temp=arrs[i]; arrs[i]=arrs[index]; arrs[index]=temp; } } public static void main(String[] args) { int[] arrs=new int[]{2,6,8,99,4,46,4,5}; System.out.println(Arrays.toString(arrs)); selectSort(arrs); System.out.println(Arrays.toString(arrs)); } }
时间复杂度O(n2),利用双重for循环,从第二个数开始遍历,然后保存待插入的数,这样有序部分则可以向后覆盖一个位置,然后里层循环 j >= 0 && temp < arrs[j] 找到合适的位置后,只需要将待插入的数插入即可。
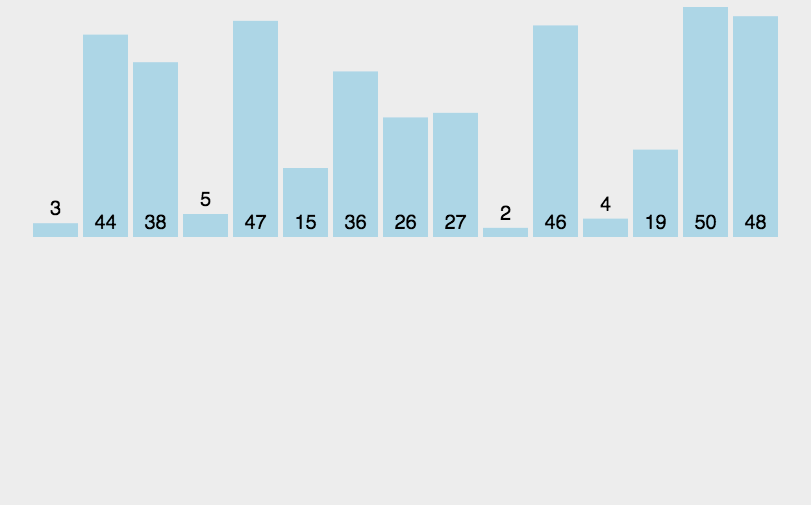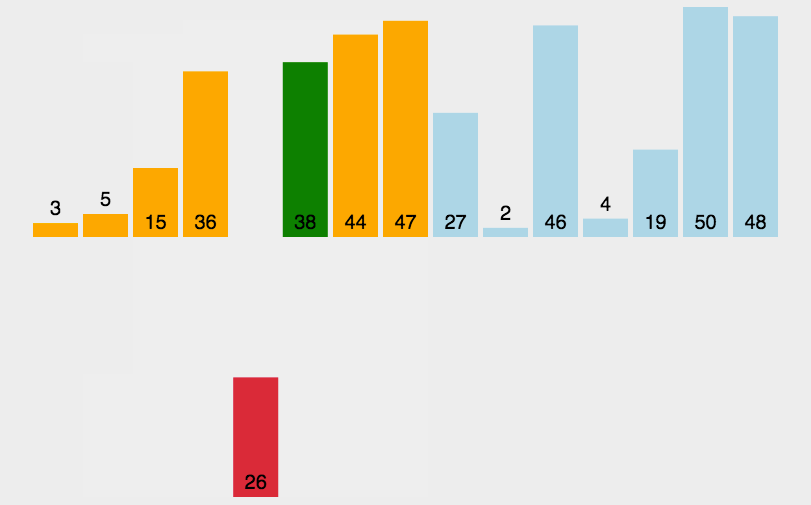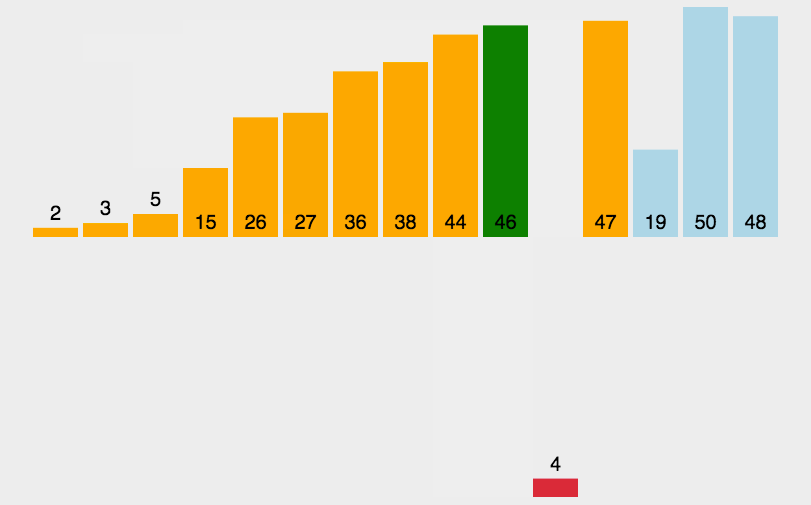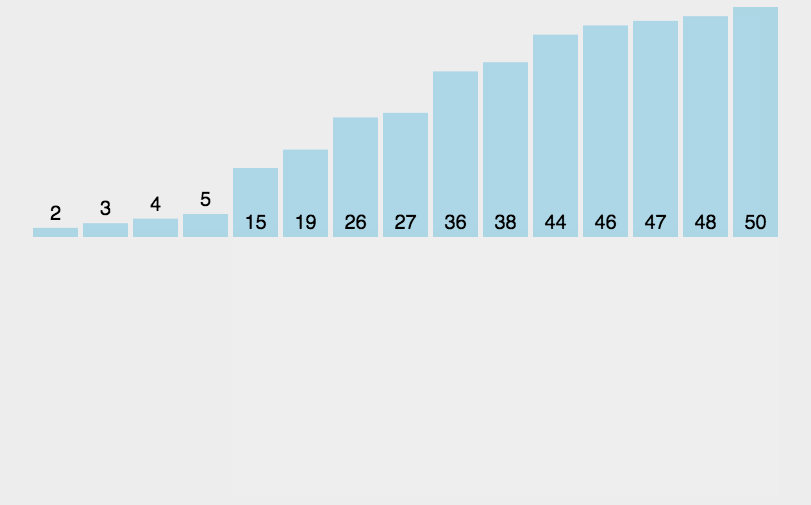
参考代码:
package edu.tyut; import java.util.Arrays; /** * 插入排序: */ public class InsertionSort { public static void insertSort(int[] arrs) { //第一个肯定是有序的,所以从第二个数开始遍历 for (int i = 1 ;i < arrs.length; i++) { int j=0; int temp = arrs[i];//取出第i给数,和前i-1个数比较,插入合适位置。 //因为前i-1个数都是从小到大的有序序列,所以只要当前比较的数arr[j]比temp大,就把这个数后移一位 for (j = i - 1; j >= 0 && temp < arrs[j]; j--) { arrs[j+1]=arrs[j];//因为第i个数已经保存为temp,所以可以向后覆盖 } //将第i个值插入到合适位置,因为交换结束后再自减运算,所以这里需要+1 arrs[j+1]=temp; } } public static void main(String[] args) { int[] arrs=new int[]{2,6,5,2,3,4,3,0,6}; System.out.println(Arrays.toString(arrs)); insertSort(arrs); System.out.println(Arrays.toString(arrs)); } }
希尔排序(Shell Sort)
时间复杂度为O(nlogn),该方法因DL.Shell于1959年提出而得名。超越了O(n2)的算法的历史。他是在直接插入排序的增强,将记录按步长gap分组,然后在分组内进行直接插入排序。不稳定算法。
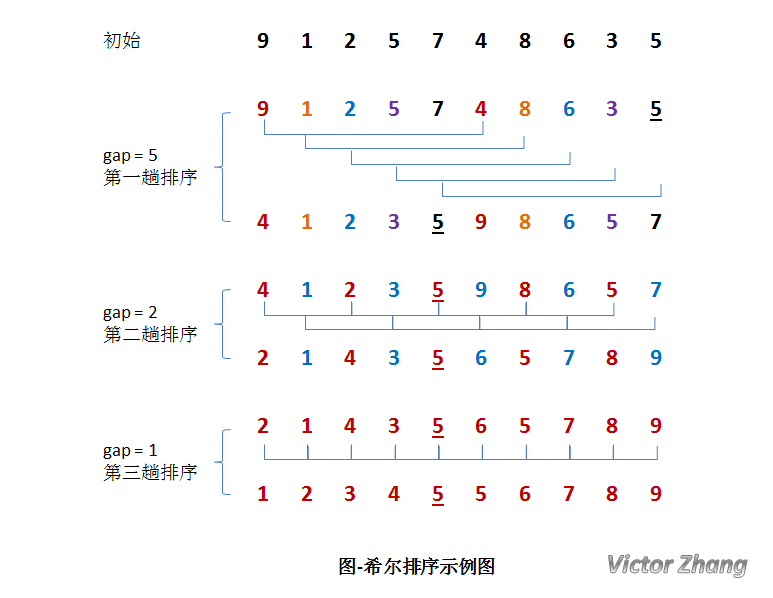
参考代码:
package edu.tyut; import java.util.Arrays; /** * 希尔排序:在直接插入排序的基础上,将记录按步长进行分组 * 所以可知,直接插入排序相当与步长为1的希尔排序 */ public class ShellSort { public static void shellSort(int[] arrs) { //初始化步长为数组长度的一半 int gap = arrs.length / 2; //循环结束条件,当gap<1是,循环结束,即排序结束 while (gap >= 1) { //把距离为gap的元素编为一个组,扫描所有组 for (int i = gap; i < arrs.length; i++) { int j = 0; int temp = arrs[i];//保存待插入元素,以便组内元素向后移动覆盖 //对距离为gap的组内元素进行直接选择排序 for (j = i - gap; j >= 0 && temp < arrs[j]; j = j - gap) { arrs[j+gap]=arrs[j]; } //将待插入元素插入合适位置 arrs[j+gap]=temp; } //一次循环结束,所有分组均已完成直接选择排序,则可将将距离缩小为原本的一半 gap=gap/2; } } public static void main(String[] args) { int[] arrs=new int[]{3,6,8,4,6,7,9,8,7,5}; System.out.println(Arrays.toString(arrs)); shellSort(arrs); System.out.println(Arrays.toString(arrs)); } }
堆排序:就是利用堆进行排序的方法。它的基本思想是,将待排序的序列构造成一个大顶堆。此时,整个序列的最大值就是堆顶的根结点,将它移走(其实就是将其与堆数组的末尾元素交换,此时末尾元素就是最大值),然后将剩余的n-1给序列重新构造成一个堆,这样就会得到n个元素中的次小值。如此反复执行,便能得到一个有序序列。--------用直接插入排序,将数组调整为堆结构,然后再简单选择排序,选择最值交换,再调整堆结构。


参考代码:
package edu.tyut; import java.util.Arrays; /** * 堆排序:利用堆(顺序存储的完全二叉树)进行排序,每次取出堆顶最值后,对堆进行调整,使堆顶元素(根结点)为最值 * 先用简单选择排序筛选出子节点中的最小值,然后通过直接插入排序,将父结点(待插入的值)插入到合适的位置。 */ public class HeapSort { /** * 将数组调整为符合堆规律的结构 * @param arr 传入需要调整的数组 * @param parent 父结点 * @param length 需要调整的数组长度 */ public void heapAdjust(int[] arr, int parent, int length) { int temp = arr[parent];//先保存父结点的值,以便后续移动交换 int child = parent * 2 + 1;//先获取到该父结点的左子结点 while (child < length) { //如果存在右子结点,且右子结点大于左子结点,则选取右子结点 if (child + 1 < length && arr[child] < arr[child + 1]) { child++; } //判断父结点(待插入的值)是否比子节点大 if(temp>arr[child]){ break;//父结点大,结束当前循环 }else { /*此处类似与直接插入排序的思想*/ arr[parent]=arr[child];//将子结点的值覆盖父节点的值 parent=child; child=child *2+1; } } //此时已经找到合适的位置,将待插入的值插入合适的位置 arr[parent]=temp; } /** *堆排序 * @param list */ public void shellSort(int[] list){ /*循环建立初始堆,初始父结点为数组的一半,即完全二叉树的最右下的父结点, 然后递减,依次向上调整,这样任意指定父结点调整时,下面的子节点已经是符合堆规律的*/ //循环建立初始化堆 for (int i = list.length/2; i >=0 ; i--) { heapAdjust(list,i,list.length); } //进行n-1次循环,完成排序,这里类似于选择排序的思想 for (int i = list.length-1; i >0; i--) { //将最大值list[0]与最后一个元素交换 int temp=list[i]; list[i]=list[0]; list[0]=temp; //交换完之后,最大值已经在底层数组的末尾,然后将交换后的堆进行调整 heapAdjust(list,0,i);//注意这里的长度已经-1了,所以堆调整不包含最后一个元素 } } public static void main(String[] args) { int[] arr=new int[]{2,6,4,9,2,3,54,1,6,166,52,6,656,54,451,6,56}; System.out.println(Arrays.toString(arr)); HeapSort heapSort=new HeapSort(); heapSort.shellSort(arr); System.out.println(Arrays.toString(arr)); } }
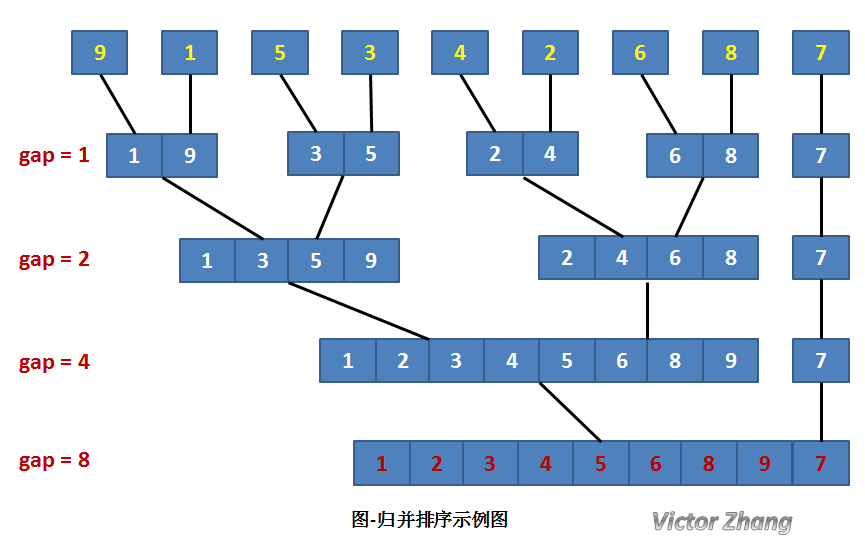
通俗概述:将无序数组进行两两分段,并将相邻两段进行比较排序,最后扩大步长归并结果。
参考代码:
package edu.tyut; import java.util.Arrays; /** * 归并排序 */ public class MergeSort { //在各段内进行排序 private void mergeSort(int[] arr, int low, int mid, int high) { int i = low; // i是第一段序列的起始索引 int j = mid + 1; // j是第二段序列的起始索引 int k = 0; // k是临时存放合并序列的下标 int[] arr2 = new int[high - low + 1]; // arr2是临时合并序列 // 扫描第一段和第二段序列,直到有一个扫描结束 while (i <= mid && j <= high) { // 判断第一段和第二段取出的数哪个更小,将其存入合并序列,并继续向下扫描 if (arr[i] <= arr[j]) { arr2[k] = arr[i]; i++; k++; } else { arr2[k] = arr[j]; j++; k++; } } //最完美的情况就是左右两边都同时扫描完添加进序列,但情况总是一边先结束扫描 // 若第一段序列还没扫描完,将其全部复制到合并序列 while (i <= mid) { arr2[k] = arr[i]; i++; k++; } // 若第二段序列还没扫描完,将其全部复制到合并序列 while (j <= high) { arr2[k] = arr[j]; j++; k++; } // 将合并序列复制到原始序列中 for (k = 0, i = low; i <= high; i++, k++) { arr[i] = arr2[k]; } } //对数组进行分段 private void mergeDiv(int[] arr, int gap, int length) { int i; // 归并gap长度的两个相邻子表 //因为数组索引是从0开始,所以起始索引为0,步长范围内最大索引为i+2*gap-1,中索引为i+gap-1 for (i = 0; i + 2 * gap - 1 < length; i +=(2 * gap) ){ mergeSort(arr, i, i + gap - 1, i + 2 * gap - 1); } // 特殊情况处理,若为奇数表,余下两个子表,后者长度小于gap if (i + gap - 1 < length) { mergeSort(arr, i, i + gap - 1, length - 1); } } public void sort(int[] arr) { if(arr==null){ return; } //首先初始化步长为1,然后2倍增长,与快速排序相反 for (int gap = 1; gap < arr.length; gap = 2 * gap) { mergeDiv(arr, gap, arr.length); } } public static void main(String[] args) { int[] arr = {2,2,5,5,46,8,9,32,5,6,24,6}; MergeSort mergeSort = new MergeSort(); System.out.println("排序前:"+Arrays.toString(arr)); mergeSort.sort(arr); System.out.println("排序后:"+Arrays.toString(arr)); } }
快速排序(Quick Sort)
快速排序是一种交换排序。快速排序由C. A. R. Hoare在1962年提出。
它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分:分割点左边都是比它小的数,右边都是比它大的数。然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归 进行,以此达到整个数据变成有序序列。
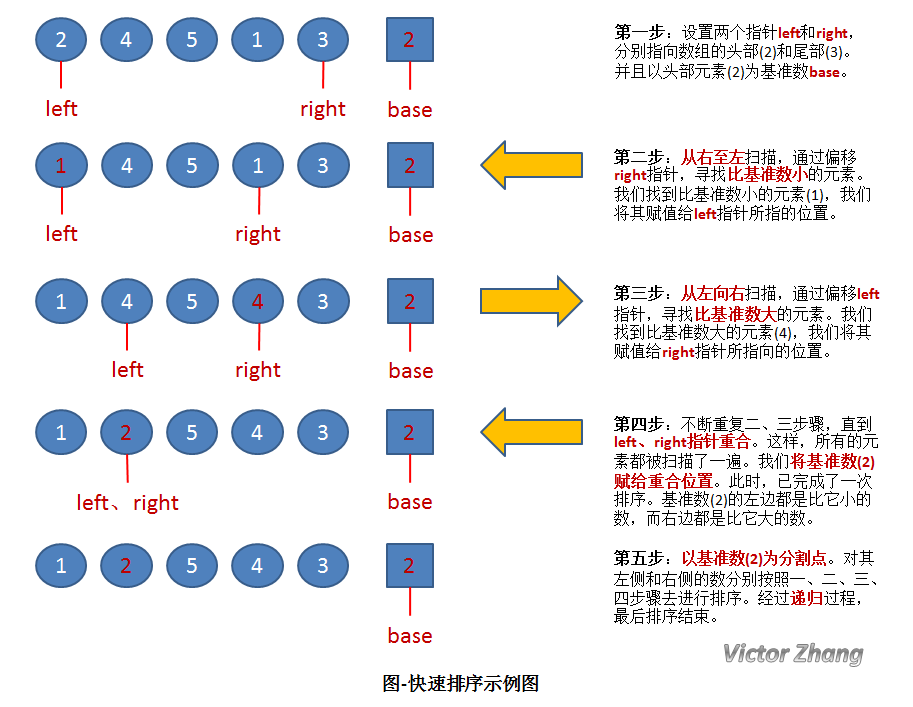
参考代码:
package edu.tyut; /** * 快速排序 */ public class QuickSort { public static void quickSort(int[] arr, int left, int right) { int i = left, j = right, base = arr[left]; while (i < j) { while (i < j && arr[j] >= base) j--; if (i < j) arr[i++] = arr[j]; while (i < j && arr[i] <= base) i++; if (i < j) arr[j--] = arr[i]; } arr[i] = base; // i~j 之间的数据就已经顺序了 if (i > left) quickSort(arr, left, i - 1);// 计算 left ~ i-1 if (j < right) quickSort(arr, j + 1, right);// 计算 j+1 ~ right } public static void printArry(int[] nums) { System.out.print("{ "); for (int i = 0; i < nums.length; i++) { System.out.print(nums[i] + " "); } System.out.println("}"); } public static void main(String[] args) { int[] arr = {2, 5, 5, 4, 6, 44, 9, 65, 62, 6, 9, 56, 56, 2, 62, 65, 95, 5, 23, 9, 562, 6, 95, 6, 59, 465, 65, 95, 9}; printArry(arr); quickSort(arr, 0, arr.length - 1); printArry(arr); } }
*Java系统提供的Arrays.sort函数。对于基础类型,底层使用快速排序。对于非基础类型,底层使用归并排序。请问是为什么?
答:这是考虑到排序算法的稳定性。对于基础类型,相同值是无差别的,排序前后相同值的相对位置并不重要,所以选择更为高效的快速排序,尽管它是不稳定的排序算法;而对于非基础类型,排序前后相等实例的相对位置不宜改变,所以选择稳定的归并排序。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号