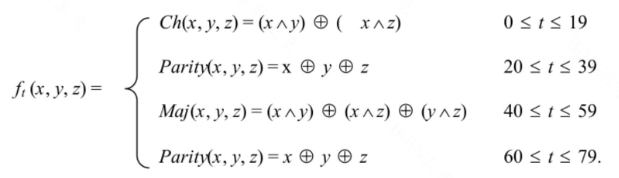5.3 SHA-1

5.3 SHA-1

与MD4相似

算法描述

• 算法的输入:小于2^64比特长的任意消息，分为512比特长的分组。
• 算法的输出:160比特长的消息摘要。
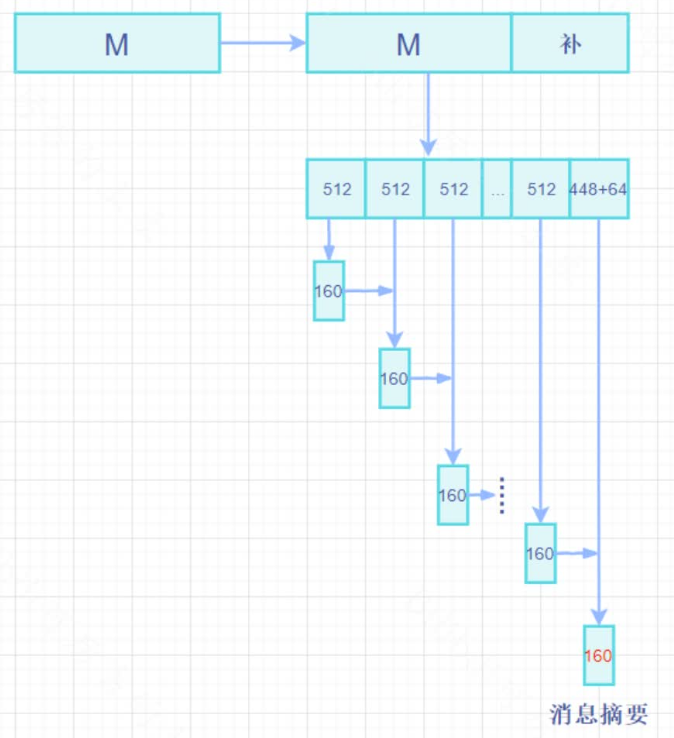
• 算法的框图与MD5一样，但杂凑值的长度和链接变量的长度为160比特

B站视频--讲解得非常好（已三连）

https://www.bilibili.com/video/BV1Ua411679P?spm_id_from=333.337.search-card.all.click

步骤简述：

• 补位——使得所有长度都为512bit
• 对分组（每个512bit）处理
• 对第一个512bit，给一个初始的缓冲区连接变量ABCDE，然后第一个512bit，会得到160bit
• 第一步产生的160bit成为第二步的链接变量ABCDE，与第二步的512bit运算，会得到160bit
• 由此不断重复，得到最终的160bit

1、对消息填充

• 对消息填充，使得其比特长在模512下为448，即填充后消息的长度为512的某一倍数减64，留出的64比特，给第二步。

  • 注：步骤1是必需的，即使消息长度已满足要求，仍需填充。

• 例如，消息长为24bit，则要填充1个1，423个0，最后留下64bit的空缺。

• 留下64位，能表达的最大的数字是2^64 -1，（为什么可以表示原先的长度啊喂！！）

  

2、附加消息长度

• 第一步留出的64比特用来表示消息被填充前的长度。
• 如果消息长度大于2^64，则以264为模数取模。

3、对MD缓冲区初始化

• 使用160比特长的缓冲区存储中间结果和最终杂凑值。缓冲区为5个32比特以big-endian方式存储数据的寄存器【十六进制】
• big-endian模式是指数据的高字节保存在内存的低地址中，反之为little-endian模式

4、分组处理

扩充

前16个是照抄M，后面的W就需要依次计算得出。

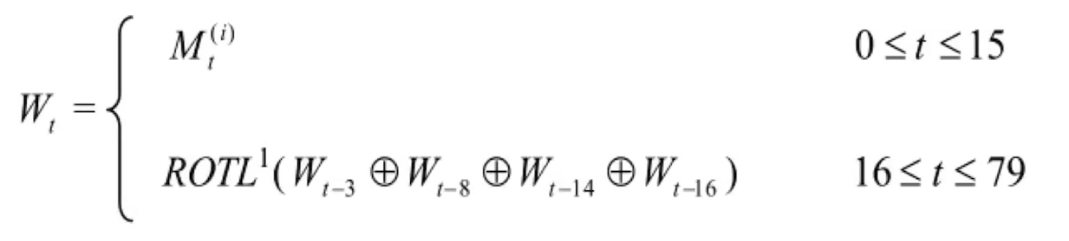
• 原有 512bit = 16个 32bit M[0],M[1]......M[15]
• 扩充后！！
• ​ 80个 32bit W[0], W[1]......W[79]

sha1有四轮运算，每一轮有20=个，然后产生160bit，者160bit的消息摘要存放在5个32bit的链接变量中

其中这个过程的加法是模2^32的

80轮运算

也就是说，对abcde依次进行了某种运算，abcde得到一个新的值。 这样运算80轮

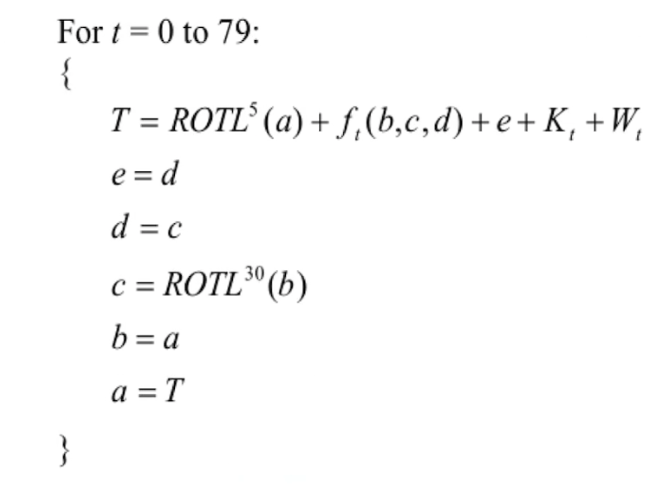
对80轮运算 其中的T的解释

• ROTL^5 五次左移运算
• ft是轮函数，根据t的不同变化
  • 
• Kt是常量函数，也是跟t有关
  • 

5、输出第一个512bit产生的160bit摘要消息（进入下一轮）

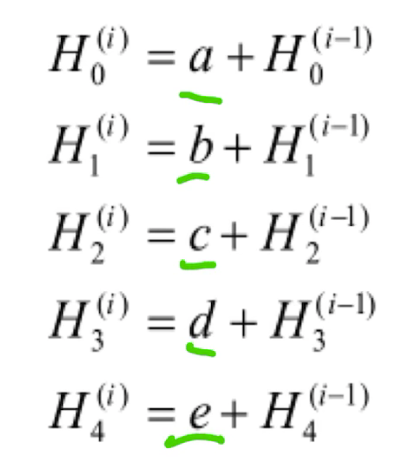
操作

• abcde是80轮运算后得到的。
• 右边的H0 - H4 是初始链接变量
• 左边的H0 -H4 就是第一个160bit的输出

是否为多余1个512bit的分组

• 若此处只有一个512bit的分组，则到这里就结束了
• 但是如果很多个512bit