2.7 m-序列的安全性

2.7 m-序列的安全性

即寻找m序列的递推关系式。

已知一段序列，如果知道其反馈多项式，就可以将其后的序列依次求出，那反馈多项式呢？

方法

• 解方程
  • 已知序列{a}是由n级线性移存器产生的，并且知道{a}的连续2n位，可用解线性方程组的方法得到反馈多项式
• 线性反馈移位寄存器综合解——B-M算法
  • 套方法，一项项计算，按步骤走。

解方程

异或解方程

矩阵解方程

这里c与a挨个相乘，就是包含了所有情况，去解一个大方程。

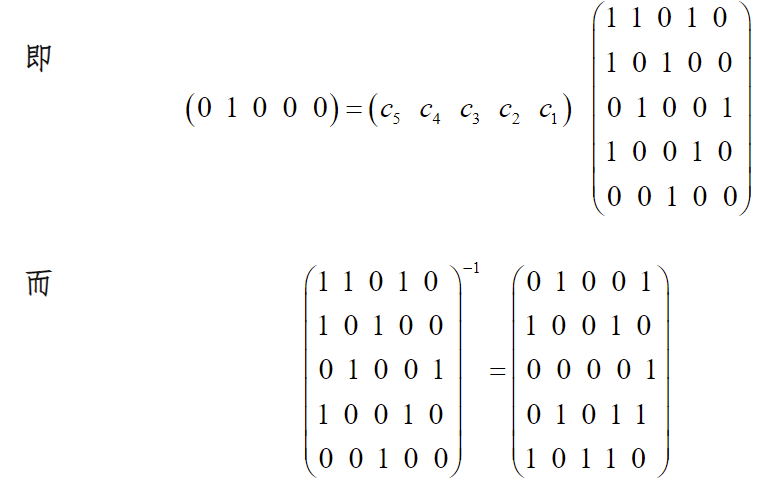
线性反馈移位寄存器综合解

线性移位寄存器的综合问题可表述为:给定一个N长的二元序列a，如何求出产生这一序列的最小级数的线性移位寄存器，即最短的线性移位寄存器。【最短：重构密钥序列所必须付出的最小代价】

准备

B-M算法

算法中规定：

• 在特征多项式f(x)中要求C0=1
• 规定:0级线性移位寄存器是以f(x)=1为特征多项式的线性移位寄存器，且n长(n=1,2,..., N)全零序列，仅由0级线性移位寄存器产生。

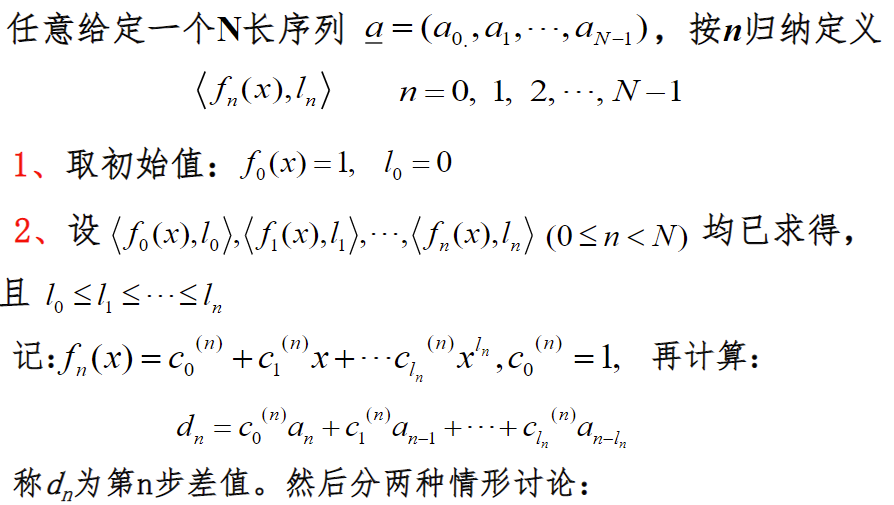
例

密钥流生成器的设计原则

• 长周期
• 高线性复杂度
• 统计性能良好
• 足够的“混乱”
• 足够的“扩散”
• 抵抗不同形式的攻击