2.5 m-序列

2.5 m-序列

• 线性反馈移位寄存器的多项式表示
• m-序列产生的条件

线性移位寄存器----> 一元多项式表示

生成函数

对于一个给定序列{a}，其幂级数，就是生成函数

\[A(x) =\sum_{i=1}^{∞}{a_i}{x_i} \]

定理2.1：生成函数

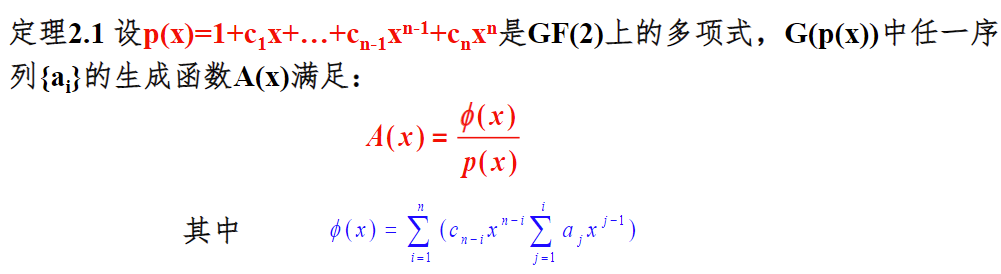
证明

这里的第二行不太明白。

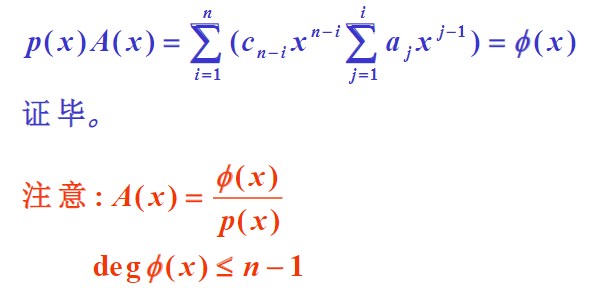
定义：G(p(x))、p(x)的周期

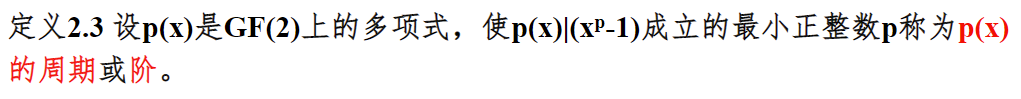
定理：LFSR的级数

定理：输出序列的r只与p(x)有关

m-序列产生的条件

不可约多项式 用到了泰勒展开式

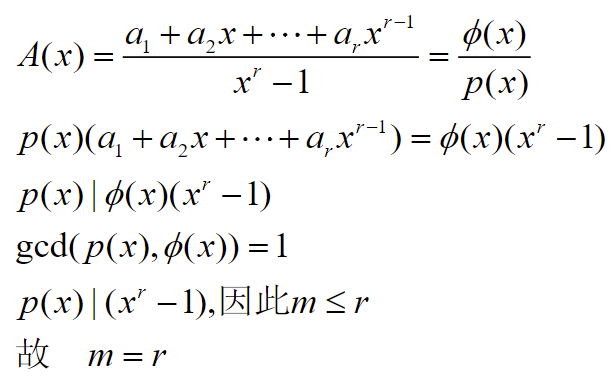
定理：产生序列有最大周期，则P(x)必不可约；反之不可

例

定理：序列为m-序列 ⇔ P(x)阶达（2^n）-1

m-序列举例

最后的这个输出，左移三位就能得到前面的。