2.3二元序列的伪随机性

2.3二元序列的伪随机性

• 二元序列的相关概念
• 伪随机序列

二元序列

GF（2）上由一个无限序列如下，这就是二元序列，每个a 都∈GF（2）

\[\vec{a} = (a_1,a_2,....,a_n,....) \]

周期

对于一个二元序列，当存在正整数l，对于一切正整数k都有如下情况，则称a是周期的

\[a_k = a_k+_l \]

满足上述条件的最小正整数称为a的周期，记作

\[p(\vec{a}) \]

周期的性质

游程

• 设a是GF（2）上周期为p（a）的周期序列，让a的一个周期依次排列头尾相连
• 这一连串两两相邻的项分别称为a的一个周期中一个1游程或一个0游程。
• 而1游程中1的个数或0游程中0的个数称为游程的长度。

【例】

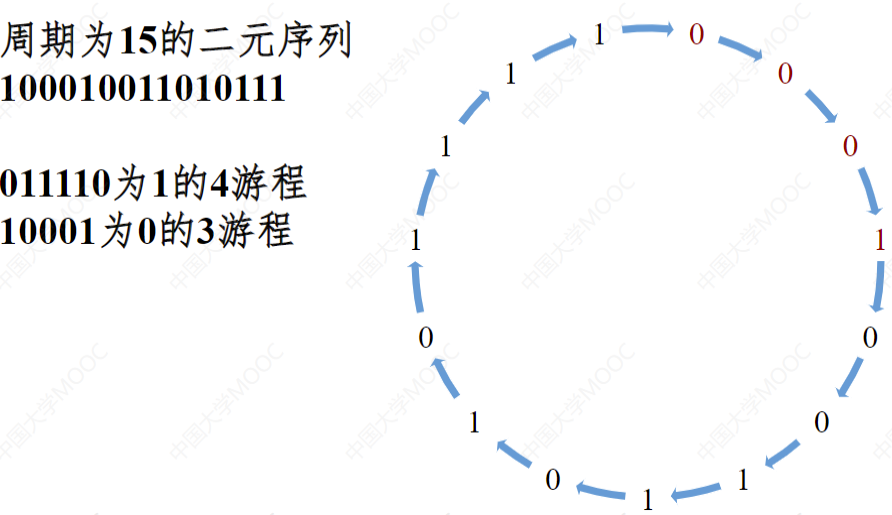
自相关函数

伪随机序列

Golomb伪随机公设

• 在序列的一个周期内，0与1的个数相差至多为1。
  • 说明{a}中0与1出现的概率基本上相同
• 在序列的一个周期内，长为i的游程占游程总数的1/2^i(i=1,2,…)，且在等长的游程中0的游程个数和1的游程个数相等。
  • 说明0与1在序列中每一位置上出现的概率相同
• 异相自相关函数是一个常数。
  • 意味着通过对序列与其平移后的序列做比较，不能给出其他任何信息

伪随机序列定义

对于一个GF（2）上有周期的序列，当R(t) = -1 ，则称a为伪随机序列

【例】

伪随机序列还应满足的条件