ICLR 2022: Anomaly Transformer论文阅读笔记+代码复现

本论文全名为Anomaly Transformer: Time Series Anomaly Detection with Association Descrepancy（通过关联差异进行时序异常检测），主要提出了一种无监督的异常点检测算法，并在6个benchmarks上测试，获取良好结果。

论文链接：ANOMALY TRANSFORMER: TIME SERIES ANOMALY DETECTION WITH ASSOCIATION DISCREPANCY

论文主要想法

作者这里定义了两个概念：prior-association与series-association，用于捕捉时间序列数据中的异常模式和正常模式。

  • 将Transformers应用于时间序列，通过Transformer模型的自注意力（self-attention map），获取每个时间点的时许关联，即于整个时间序列的关联权重分布。这个关联分布可以为整个时序上下文提供丰富的描述，展示动态模式，例如周期或趋势，此关联分布被定义为序列关联（series association）；
  • 作者还观察到，由于异常点和正常点相比十分稀少，异常点的比较难与整个序列建立关联，但由于连续性，异常点更有可能与其相邻的时间点建立强关联。这种 adjacent-concentration inductive bias （临近集中传导偏差）被称为先验关联（prior-association）。

基于以上观察和概念，作者发现：时序中的异常位置的关联应集中在相邻的时间点上，这些时间点由于连续性而更可能包含类似的异常模式。相比之下，占主导地位的正常时间点可以发现与整个系列的信息关联，而不限于相邻区域。

这样产生了新的概念：关联差异（Association Discrepancy），这指的是每个时间点的prior-association与series-association距离的量化。作者希望通过利用“异常点的关联更加相邻集中”这一点，判断出比较小的关联差异，进行无监督异常点识别。

如何计算：

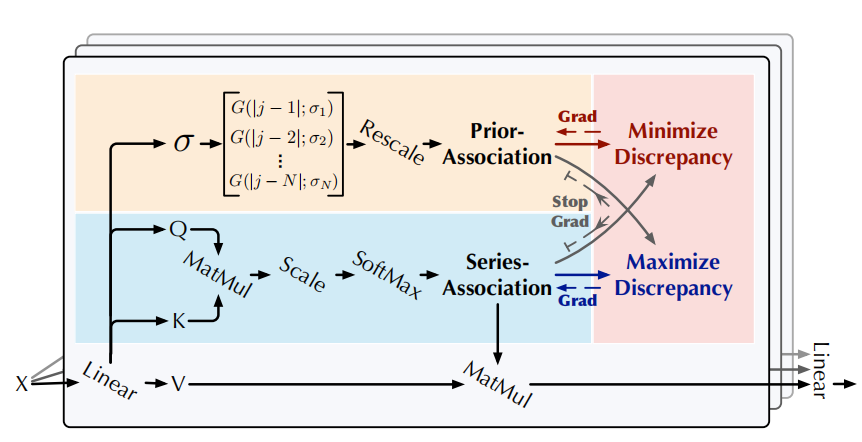
  • 作者将Transformer中的self-attention机制更新为Anomaly-Attention机制，命名为Anomaly transformer，并采用一个双分支的结构来对先验关联、序列关联进行建模。
  • Prior-association：通过可学习的高斯核（learnable Gaussian kernel）来计算；
  • Series-association来自于原本序列中的自关联权重（self-attention weight）。

此外，采用minimax机制来作用于双分支结构，来放大Association Discrepancy的可区分性，并进一步推导出新的基于关联的准则。

相关领域其他工作：

  1. 无监督时间序列异常检测
    • 密度估计方法：计算了局部密度和局部连接性来判断是否是outlier（LOF，COF）或者说使用高斯混合模型来预测密度（DAGMM，MPPCACD）；
    • 聚类方法：通过点到聚类中心的距离来计算anomaly score；
    • 重构方法：计算reconstruction error，例如LSTM-VAE模型和GAN模型；
    • 自回归方法：计算prediction error，例如延展了ARIMA模型的VAR模型（通过 lag-dependent covariance预测未来数据），或者LSTM。
  2. 在时间序列分析中transformers的运用
    • 由于self-attention 机制，transformers在时间序列分析中有广泛运用，比如用于发现可靠的长期时间依赖性。
    • 在时序异常检测中，GTA（Graph Transformer Autoencoder）模型利用Transformers来学习多个物联网传感器之间的关系、并提供了为时序异常检测提供了重构基准。

算法解读

模型结构

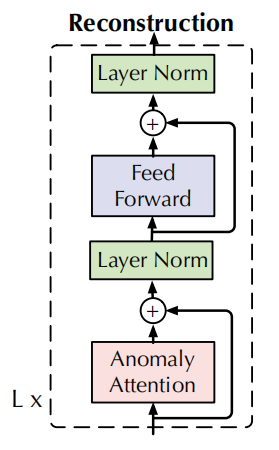
假设我们有L层，一层模型结构为：

img

计算步骤为：

\[\begin{aligned} & \mathcal{Z}^l=\text { Layer-Norm }\left(\text { Anomaly-Attention }\left(\mathcal{X}^{l-1}\right)+\mathcal{X}^{l-1}\right) \\ & \mathcal{X}^l=\text { Layer-Norm }\left(\text { Feed-Forward }\left(\mathcal{Z}^l\right)+\mathcal{Z}^l\right) \end{aligned} \]

以下公式被总结为Anomaly-Attention(·):

\[\begin{aligned} & \text{Initialization}: \mathcal{Q}, \mathcal{K}, \mathcal{V}, \sigma=\mathcal{X}^{l-1} W_{\mathcal{Q}}^l, \mathcal{X}^{l-1} W_{\mathcal{K}}^l, \mathcal{X}^{l-1} W_{\mathcal{V}}^l, \mathcal{X}^{l-1} W_\sigma^l \\ & \text{Prior-Association}: \mathcal{P}^l=\operatorname{Rescale}\left(\left[\frac{1}{\sqrt{2 \pi} \sigma_i} \exp \left(-\frac{|j-i|^2}{2 \sigma_i^2}\right)\right]_{i, j \in\{1, \cdots, N\}}\right) \\ & \text{Series-Association}: \mathcal{S}^l=\operatorname{Softmax}\left(\frac{\mathcal{Q K}^{\mathrm{T}}}{\sqrt{d_{\text {model }}}}\right) \\ & \text{Reconstruction}: \widehat{\mathcal{Z}}^l=\mathcal{S}^l \mathcal{V} \end{aligned} \]

算法图参考：

img

通过KL-Divergence来计算Association Discrepancy：

\[\operatorname{AssDis}(\mathcal{P}, \mathcal{S} ; \mathcal{X})=\left[\frac{1}{L} \sum_{l=1}^L\left(\operatorname{KL}\left(\mathcal{P}_{i,:}^l \| \mathcal{S}_{i,:}^l\right)+\mathrm{KL}\left(\mathcal{S}_{i,:}^l \| \mathcal{P}_{i,:}^l\right)\right)\right]_{i=1, \cdots, N} \]

  • 这里我们使用先序关联、序列关联的对称KL散度来代表这两个分布之间的information gain（信息增益）
  • AssDis（P，S；X）为一个N*1的数组，每一行代表了每个时间点的association discrepancy，对应了输入点的数据X_i
  • 之前的观察可以得出，异常点比起正常点会有较小的AssDis值。

模型优化：minimax

对于非监督学习一般使用重构损失（Reconstruction loss）来进行优化，重建损失将引导序列关联找到最有信息量的关联。

loss函数：

\[\mathcal{L}_{\text {Total }}(\widehat{\mathcal{X}}, \mathcal{P}, \mathcal{S}, \lambda ; \mathcal{X})=\|\mathcal{X}-\widehat{\mathcal{X}}\|_{\mathrm{F}}^2-\lambda \times\|\operatorname{AssDis}(\mathcal{P}, \mathcal{S} ; \mathcal{X})\|_1 \]

为了增强与普通时间点的区别，作者还增加了一项来使关联差异更大，由于prior-association的单峰性，discrepancy loss会引导series-association更加关注不相邻的区域，使得异常的重构更加困难，异常的可识别性更强。

  • \(\|\cdot\|_{\mathrm{F}}^2\) 为Frobenius-norm（F-范数）
  • 在这里，loss function采用F-范数的主要原因可能是为了衡量重构误差的大小。

Minimax 策略：由于直接最大化关联差异会导致高斯核的scale参数急速减小，先序序列会变得无意义，因此作者提出了minimax策略：

img

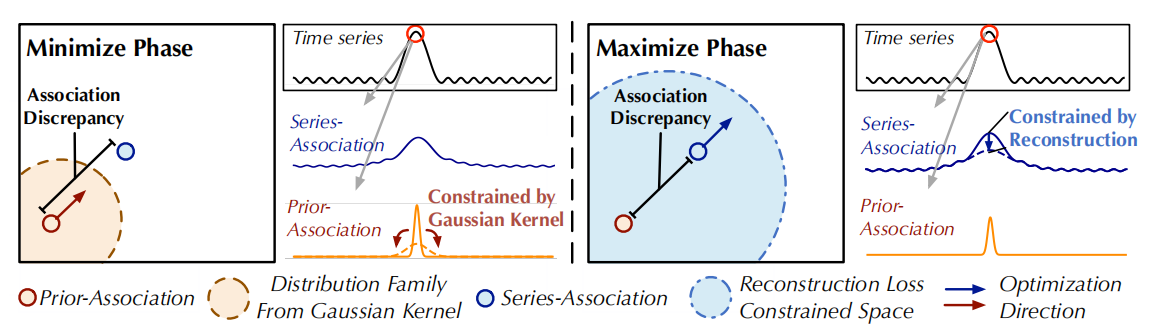
  • 在最小化阶段，用先序序列将关联差异在高斯核分布中最小化；最大化阶段，获取在重构损失中的最优关联序列，来获取最大化的关联差异。
  • 这样的流程迫使关联序列更关注不相邻的水平。

公式

\[\text{Minimize Phase: }\mathcal{L}_{\text{Total}}(\hat{\mathcal{{X}}}, \mathcal{P},\mathcal{S}_{\text{detach}} ,-\lambda; \mathcal{X}) \\ \text{Maximize Phase: }\mathcal{L}_{\text{Total}}(\hat{\mathcal{{X}}}, \mathcal{P}_{\text{detach}}, \mathcal{S}, \lambda; \mathcal{X}) \]

  • detach指的是停止关联的梯度反向传播。由于P在最小化阶段逼近\(S_{\text{detach}}\)，最大化阶段将对series-association产生更强的约束，迫使时间点更多地关注非相邻区域。在重建损失下，异常比正常时间点更难实现，从而放大了关联差异的正常-异常可区分性。

基于关联的异常评判标准

在重构标准中，我们添加了正则化的关联差异，将同时利用时间表示和可区分的关联差异。最后得出的评判标准（异常分数）如下：

\[\operatorname{AnomalyScore}(\mathcal{X})=\operatorname{Softmax}(-\operatorname{AssDis}(\mathcal{P}, \mathcal{S} ; \mathcal{X})) \odot\left[\left\|\mathcal{X}_{i,:}-\widehat{\mathcal{X}}_{i,:}\right\|_2^2\right]_{i=1, \cdots, N} \]

第一部分为正则化的关联差异，第二部分为重构错误。\(\odot\) 为元素乘法

AssDis越小，异常分数越大；reconstruction error越大，异常分数越大。为了更好地重建，异常值通常会降低重构差异，导致越高的异常分数。因此这样的设计可以让重构错误核关联差异协同提高检测性能。

代码复现

1. 装环境

安装pytorch

只能在python3.6上跑，需要安装对应的pytorch（要求：Python 3.6, PyTorch >= 1.4.0）
参考 https://blog.csdn.net/yup1212/article/details/124277058 发现可能只能在1.5版本上运行，刚好满足要求
官网下载v1.5版本的指南： https://pytorch.org/get-started/previous-versions/#v151 ，可以根据自己gpu/电脑系统版本选择
我是linux，cuda版本12.2，这里选择了

conda install pytorch==1.5.1 torchvision==0.6.1 cudatoolkit=10.2 -c pytorch

但后来发现还是报错，
在 torch.autograd.backward(self, gradient, retain_graph, create_graph)
处报错：RuntimeError: no valid convolution algorithms available in CuDNN (getValidAlgorithms at /opt/conda/conda-bld/pytorch_1591914838379/work/aten/src/ATen/native/cudnn/Conv.cpp:430)

意思是无法在CuDNN中找到可用的卷积算法，看下来还是pytorch版本的问题。参考 https://blog.csdn.net/hymn1993/article/details/125558623 发现可以安装python3.7，于是重新安装。参考这篇文章的作者的选择，我安装了pytorch 1.12.1，这里选择了cuda11.3的版本：

conda install pytorch==1.12.1 torchvision==0.13.1 torchaudio==0.12.1 cudatoolkit=11.3 -c pytorch

由于我cuda版本为12.2，不能选择太低版本的比如CUDA 10.2的安装指令，会报错：

NVIDIA A100-PCIE-40GB with CUDA capability sm_80 is not compatible with the current PyTorch installation.
The current PyTorch install supports CUDA capabilities sm_37 sm_50 sm_60 sm_61 sm_70 sm_75 compute_37.
If you want to use the NVIDIA A100-PCIE-40GB GPU with PyTorch, please check the instructions at https://pytorch.org/get-started/locally/

安装其他依赖

pip install pandas scikit-learn

2. 下载数据集

根据作者在README中给到的链接，可以通过google drive获取数据集： https://drive.google.com/drive/folders/1gisthCoE-RrKJ0j3KPV7xiibhHWT9qRm?usp=sharing

3. 进行训练和测试

SMAP

这里我先选择SMAP数据集进行测试。运行 bash ./scripts/SMAP.sh 后获得测试结果：
Accuracy : 0.9906, Precision : 0.9370, Recall : 0.9935, F-score : 0.9644

SML

运行 bash ./scripts/SML.sh 后获得测试结果：

Accuracy : 0.9871, Precision : 0.9183, Recall : 0.9629, F-score : 0.9401

SMD

运行 bash ./scripts/SMD.sh 后获得测试结果：

Accuracy : 0.9916, Precision : 0.8850, Recall : 0.9161, F-score : 0.9003

PSM

运行 bash ./scripts/PSM.sh 后获得测试结果：

Accuracy : 0.9873, Precision : 0.9730, Recall : 0.9816, F-score : 0.9773

代码解读可以参考 https://blog.csdn.net/smileyan9/article/details/128439360
代码复现（讨论更多数据集）可以参考 https://cloud.tencent.com/developer/article/2373880

附录Appendix

KL 散度（Kullback-Leibler Divergence）

D_{KL}(P||Q): KL散度通常用于量化概率分布P与概率分布Q的不同。从采样角度，KL散度描述了我们用分布Q来估计数据的真实分布P的编码损失。
- 假设对某随机变量存在两个概率分布P，Q。如果该随机变量为离散，则KL散度定义为：

\[\mathbb{D}_{\mathrm{KL}}(P \| Q)=\sum_i P(i) \ln \left(\frac{P(i)}{Q(i)}\right) \]

（如果是连续则求和符号变积分符号，范围取-inf~inf）

\(D_{KL}(P\\|Q)=0\) 当且仅当\(P=Q\)

  • 关于KL散度的笔记，链接

Transformers模型

Transformers模型是一类在自然语言处理（NLP）领域广泛使用的深度学习模型。它们以注意力机制（Attention Mechanism）为核心，允许模型在处理输入数据（如文本）时动态地聚焦于信息的不同部分。
Transformers算法原理：

自注意力（Self-Attention）机制：

查询（Query）、键（Key）、值（Value）：自注意力机制通过将输入序列的每个元素转换为查询（Q）、键（K）和值（V）来工作。每个元素对于所有元素（包括自身）生成一个权重，权重决定了在生成输出时应该给予每个元素多少注意力。
注意力权重：注意力权重计算涉及Q和K的点积，然后通常使用softmax函数进行缩放，以确保权重的总和为1。

多头注意力（Multi-Head Attention）：

Transformers模型通常不只计算一组Q、K、V，而是将输入分割成多个头，每个头独立地计算一组Q、K、V，从不同的角度捕捉信息，然后将所有头的输出拼接起来，通过一个线性层得到最终的输出。这样可以让模型同时关注来自不同位置的不同信息。

位置编码（Positional Encoding）：

由于Self-Attention机制本身不包含序列的顺序信息，Transformers引入位置编码来加入序列中每个元素的位置信息。位置编码与输入元素的编码相加，这样模型就能知道序列中元素的顺序。

标准的Encoder-Decoder结构：

Encoder：编码器部分由多个相同的层组成，每层都有多头注意力和前馈神经网络（通常是全连接层）。它逐层处理输入数据，将信息向上传递。
Decoder：解码器也由多个相同的层组成，除了处理前一个解码器层的输出，每一层还需要处理编码器的输出。解码器在自注意力层使用了所谓的masked attention，确保位置i的输出只依赖于小于i的位置，保证了解码的自回归特性。

前馈神经网络（Feed-Forward Networks）：

在每个Encoder和Decoder层中，除了注意力机制外，还有一个前馈神经网络，它对每个位置应用相同的全连接层，但是独立于序列中的其他位置。这允许模型进一步整合每个位置的信息。
更多可以参考Transformer模型详解（图解最完整版）

Reconstruction loss

Reconstruction loss是机器学习中一种常见的损失函数，特别是在无监督学习和生成模型（如自编码器和生成对抗网络）中使用。它衡量的是模型重构输入数据的能力，即模型生成的输出与原始输入数据之间的差异。在不同的上下文中，重构损失可以有不同的形式和名称，但其核心目的相同：使得重构的输出尽可能接近原始输入。

在解释重构损失之前，需要了解自编码器的基本结构，它是一个典型使用重构损失的模型。自编码器通常由两部分组成：编码器和解码器。编码器的任务是将输入数据压缩成一个低维表示（称为编码），而解码器的任务是从这个低维表示重构出原始数据。

重构损失的含义：

衡量差异：重构损失计算的是重构数据（解码器的输出）与原始输入数据之间的差异。这个差异可以通过不同的方法来衡量，例如均方误差（Mean Squared Error, MSE）、交叉熵损失等。

优化目标：在训练过程中，通过最小化重构损失，模型学习到的编码会尽可能包含重建原始数据所需的全部信息，使得解码器可以更准确地重建输入数据。

应用领域：虽然重构损失在自编码器中最为常见，但它也广泛应用于其他生成模型，如变分自编码器（VAEs）和部分生成对抗网络（GANs），在这些模型中，重构损失帮助模型学习生成与真实数据分布尽可能相似的数据。

常见的重构损失类型：

均方误差（MSE）：衡量的是重构值与真实值之间差的平方的平均值，常用于回归问题和连续数据的重构。
交叉熵损失：在处理分类问题或模型输出是概率分布时常用，它衡量的是两个概率分布之间的差异。
重构损失在模型的训练过程中起到至关重要的作用，它直接影响模型的重构质量和学习到的特征的有效性。通过最小化重构损失，可以使得模型在各种任务，如降维、去噪、生成模型等方面表现得更好。

Reference

posted @ 2024-01-05 18:04  落魄统计佬  阅读(2727)  评论(3)  编辑  收藏  举报