哈夫曼树
1.定义
1.1 哈夫曼树
哈夫曼树是一种最基本的压缩编码方法。对于如图所示的两棵二叉树,每个叶子节点都带有权值:

从树中一个结点到另一个结点之间的分支构成两个结点之间的路径,路径上的分支数目称作路径长度。例如,树 a 中根节点到结点 D 的路径长度为 4,树 b 中根节点到结点 D 的路径长度为 2。树的路径长度就是从树根到每一结点的路径长度之和。因此,树 a 的路径长度就为 20,树 b 的路径长度为 16。
如果考虑到带权的结点,结点的带权的路径长度为从该结点到树根之间的路径长度与结点上权的乘积。树的带权路径长度为树中所有叶子结点的带权路径长度之和。
例如,树 a 的 \(WPL=5*1+15*2+40*3+30*4+10*4=315\)。而树 b 的 \(WPL=5*3+15*3+40*2+30*2+10*2=220\)。
其中,【带权路径长度(WPL)】最小的二叉树称作【哈夫曼树】,也称作最优二叉树。
将树 a 转化为哈夫曼树的步骤如下:
- 首先把带有权值的叶子结点按照从小到大的顺序排列成一个有序序列,即:A5,E10,B15,D30,C40。
- 然后取头两个最小权值的结点作为一个新结点 N1 的两个孩子结点,注意相对较小的是左孩子,这里 A 是 N1 的左孩子,E 为 N1 的右孩子。则新节点的权值为两个叶子结点的权值的和,即 5+10=15。
- 然后将 N1 替换 A 与 E,插入有序序列中,保持从小到大的顺序排列。即 N115,B15,D30,C40。
- 重复步骤 2。将 N1 与 B 作为一个新的结点 N2 的两个子结点。N2 的权值为 15+15=30。
- 重复上述步骤,直到排列完成。
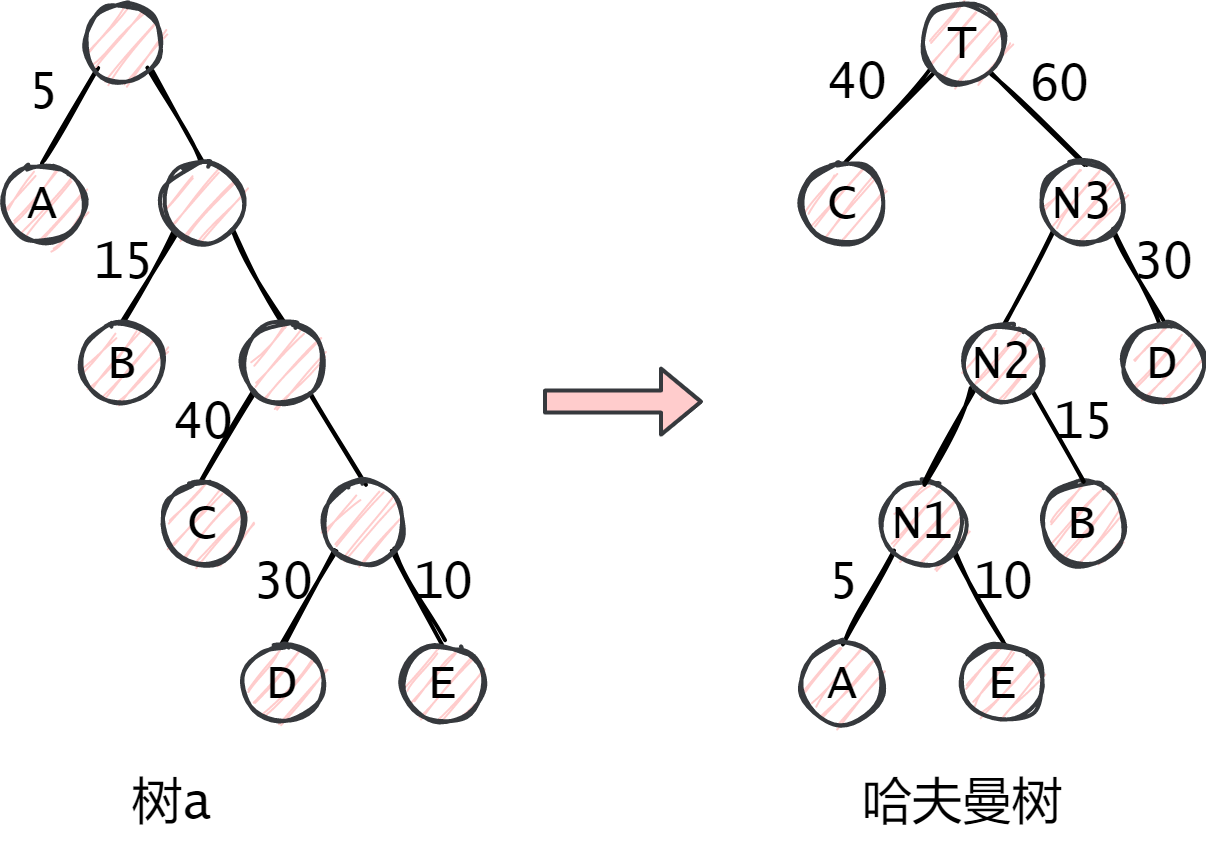
此时哈夫曼树的 \(WPL=40*1+30*2+15*3+10*4+5*4=205\)。
1.2 哈夫曼编码
哈夫曼树最早应用于电文编码。一般地,设需要编码的字符集为 \(d_1,d_2,……,d_n\),各个字符在电文中出现的次数或者频率集合为 \(w_1,w_2,……,w_n\),以 \(d_1,d_2,……,d_n\) 作为叶子结点,以 \(w_1,w_2,……,w_n\) 作为相应叶子结点的权值来构造一棵哈夫曼树。规定哈夫曼树的左分支代表 0,右分支代表 1,则从根结点到叶子结点所经过的路径分支组成的 0 和 1 的序列为该结点对应字符的编码,这就是哈夫曼编码。
其编码过程如下图所示:

哈夫曼编码不同于 ASCII 和 Unicode 这些字符编码,这些字符集中的码长都采用的是长度相同的编码方案,而哈夫曼编码使用的是变长编码,而且哈夫曼编码满足立刻可解码性(就是说任一字符的编码都不会是另一个更长字符编码的前缀),这样当一个字符的编码中的位被接收时,可以立即进行解码而无须等待之后的位来决定是否存在另一个合法的更长的编码。例如,下面两个表中,表 1 不满足立刻可解码性,而表 2 则满足:
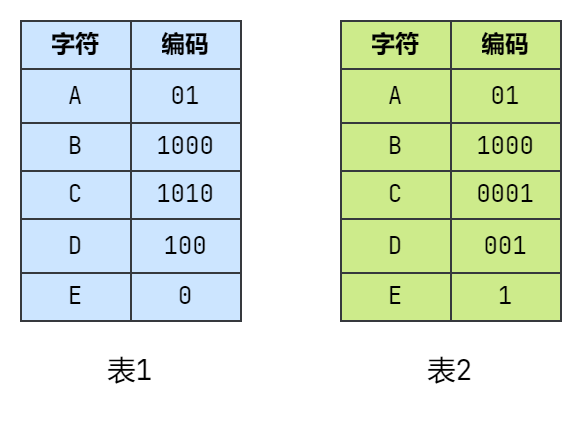
因为哈夫曼编码中每一个字符都位于哈夫曼树的叶子节点中,所以不会存在路径包含问题,这也就是立刻可解码性的原因。
为什么有时候采用哈夫曼编码压缩小文件时文件大小会变大?原因是在采用哈夫曼编码对文件内容进行逐字节编码后,不仅需要按位存储编码后的内容,还需要把原始文件中的字节数据以及权值信息存储到压缩文件当中。有了这些信息才可以在解码时正确构建哈夫曼树,然后进行解码过程。
2.代码实现
2.1 节点定义
哈夫曼树的节点定义如下:
struct Node {
Node(char data, uint weight)
: data_(data)
, weight_(weight)
, left_(nullptr)
, right_(nullptr) { }
char data_;
uint weight_; // 节点的权值
Node* left_;
Node* right_;
};
2.2 构建哈夫曼树
在构建哈夫曼树的过程中,我们不断取出序列中权值最小的两个节点,因此,我们可以使用小根堆来进行构建,其定义如下:
class HuffmanTree {
public:
HuffmanTree()
: root_(nullptr)
, minHeap_([](Node* n1, Node* n2) -> bool {
return n1->weight_ > n2->weight_;
}) {
}
private:
Node* root_;
// 存储字符对应的哈夫曼编码
unordered_map<char, string> codeMap_;
using MinHeap = priority_queue<Node*, vector<Node*>, function<bool(Node*, Node*)>>;
MinHeap minHeap_;
};
那么,构建哈夫曼树的代码如下:
void HuffmanTree::create(const string& str) {
// 先统计字符的权值
unordered_map<char, uint> dataMap;
for (char ch : str) {
dataMap[ch]++;
}
// 生成节点 放入小根堆中
for (auto& pair : dataMap) {
minHeap_.push(new Node(pair.first, pair.second));
}
while (minHeap_.size() > 1) {
// 取出两个权值最小的节点
Node* n1 = minHeap_.top();
minHeap_.pop();
Node* n2 = minHeap_.top();
minHeap_.pop();
// 生成父节点
Node* node = new Node('\0', n1->weight_ + n2->weight_);
node->left_ = n1;
node->right_ = n2;
minHeap_.push(node);
}
root_ = minHeap_.top();
minHeap_.pop();
}
2.3 构建哈夫曼编码
构建哈夫曼编码的过程可以采用前序遍历的方式进行实现,其代码如下:
void HuffmanTree::getHuffmanCode(Node* node, string code) {
if (node->left_ == nullptr && node->right_ == nullptr) {
codeMap_[node->data_] = code;
return;
}
getHuffmanCode(node->left_, code + "0");
getHuffmanCode(node->right_, code + "1");
}
2.4 编码和解码
编码的代码如下:
string HuffmanTree::encode(const string& str) {
string res;
for (char ch : str) {
res.append(codeMap_[ch]);
}
return res;
}
解码的代码如下:
string HuffmanTree::decode(const string& str) {
string res;
Node* cur = root_;
for (char ch : str) {
if (ch == '0') {
cur = cur->left_;
} else {
cur = cur->right_;
}
if (cur->left_ == nullptr && cur->right_ == nullptr) {
res.push_back(cur->data_);
cur = root_;
}
}
return res;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号