【数学】[BZOJ 3884] 上帝与集合的正确用法

---

 

Description

根据一些书上的记载，上帝的一次失败的创世经历是这样的：

第一天， 上帝创造了一个世界的基本元素，称做“元”。

第二天， 上帝创造了一个新的元素，称作“α”。“α”被定义为“元”构成的集合。容易发现，一共有两种不同的“α”。

第三天， 上帝又创造了一个新的元素，称作“β”。“β”被定义为“α”构成的集合。容易发现，一共有四种不同的“β”。

第四天， 上帝创造了新的元素“γ”，“γ”被定义为“β”的集合。显然，一共会有16种不同的“γ”。

如果按照这样下去，上帝创造的第四种元素将会有65536种，第五种元素将会有2^65536种。这将会是一个天文数字。

然而，上帝并没有预料到元素种类数的增长是如此的迅速。他想要让世界的元素丰富起来，因此，日复一日，年复一年，他重复地创造着新的元素……

然而不久，当上帝创造出最后一种元素“θ”时，他发现这世界的元素实在是太多了，以致于世界的容量不足，无法承受。因此在这一天，上帝毁灭了世界。

至今，上帝仍记得那次失败的创世经历，现在他想问问你，他最后一次创造的元素“θ”一共有多少种？

上帝觉得这个数字可能过于巨大而无法表示出来，因此你只需要回答这个数对p取模后的值即可。

你可以认为上帝从“α”到“θ”一共创造了10^9次元素，或10^18次，或者干脆∞次。

 

一句话题意：

Input

接下来T行，每行一个正整数p，代表你需要取模的值

Output

T行，每行一个正整数，为答案对p取模后的值

---

　　第一感觉：不可做- -。

　　此题十分有趣，请大家在仔细思考后再看题解- -。

　　这题有两种做法。。

　　1.出题人的做法：http://blog.csdn.net/popoqqq/article/details/43951401

　　2.另一位机智神牛的做法:我们知道，

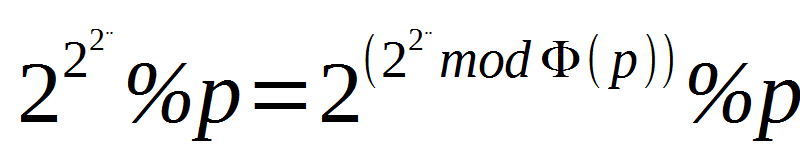 　　但是p与2不一定互质，所以我们可以化成下面的形式。

　　

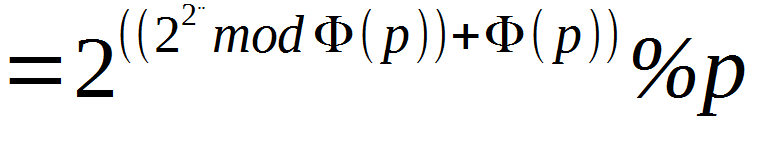
　　设f(p)=。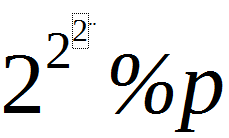

　　那么我们可以得到一个不断递推的公式f(p)=2^(f(phi(p))+phi(p))%p.边界:p=1,f(p)=0.

　　证明算法复杂度如下:

　　若p为偶数，则ϕ(p)≤p2; 
　　若p为奇数，则p存在一个奇数因子q，使得ϕ(p)存在一个偶数因子(q−1)，转化为偶数的情况。 
　　由此可知，ϕ(ϕ(...ϕ(p)))的计算经过O(logp)次的迭代就到了1，所以f(p)的计算是O(p√logp)的。（部分思(dai)想(ma)选自http://blog.csdn.net/skywalkert/article/details/43955611）

　　第二种方法的代码。。

　　

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>

#define ll long long 
using namespace std;

int mod,num[10000001];

int Qvod(int k,int mo)
{
    ll ans=1,x=2;
    while(k!=0)
    {
        if(k&1)ans=ans*x%mo;
        x=x*x%mo;
        k>>=1;
    }
    return ans;
}

int phi(int x)
{
    int ans=x,aa=x;
    for(int i=2;i<=sqrt(ans);i++)if(x%i==0){
        while(x%i==0)x/=i;
        aa=(ll)aa*(i-1)/i;
    }
    if(x!=1)aa=(ll)aa*(x-1)/x;
    return aa;
}

int f(int x)
{
    if(x==1)return 0;
    if(num[x])
        return num[x];
    int sb=phi(x);
    num[x]=Qvod(f(sb)+sb,x);
    return num[x];
}
       
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&mod);
        printf("%d\n",f(mod));
    }
    return 0;
}