【莫比乌斯反演】关于Mobius反演与gcd的一些关系与问题简化(bzoj 2301 Problem b&&bzoj 2820 YY的GCD&&BZOJ 3529 数表)

 

 

　　首先我们来看一道题

　  BZOJ 2301 Problem b

 

 

Description

　　对于给出的n个询问，每次求有多少个数对(x,y)，满足a≤x≤b，c≤y≤d，且gcd(x,y) = k，gcd(x,y)函数为x和y的最大公约数。

Input

　　第一行一个整数n，接下来n行每行五个整数，分别表示a、b、c、d、k

Output

　　共n行，每行一个整数表示满足要求的数对(x,y)的个数

Sample Input

　　2

　　2 5 1 5 1

　　1 5 1 5 2

Sample Output

　　14

　　3

HINT

　　100%的数据满足：1≤n≤50000，1≤a≤b≤50000，1≤c≤d≤50000，1≤k≤50000。

 

　　乍一看，大家的force想法:枚举x，y！之后辗转相除！！

　　但是复杂度已经爆炸。几乎是一个O(n^3)规模的算法 

　　

　　继续想！

　　我们发现:为什么要枚举所有的k啊，我们只要把k的倍数枚举一下就行了啊，然后看看两个数除以k后gcd等不等于1就行了啊。

　　这样O(n^2logn)的时间复杂度!

   

　　继续想！

　　我们求的是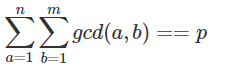

　　我们把它变换一下。。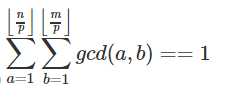

　　而在学习莫比乌斯反演的时候，我们得出了一个性质。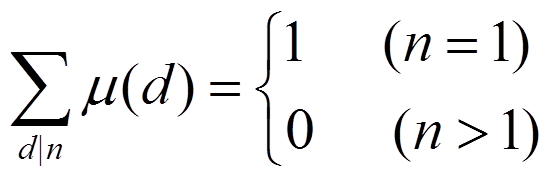

　　所以，我们把gcd(a,b)==1换成上面一行的sigma，把n改成gcd(a,b)即可。

　　变成了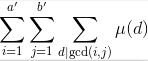

　　现在我们把第三重sigma移动到最外面。变成了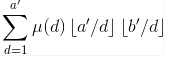(这一步需要仔细思考，要配合容斥原理)

　　复杂度为O(n^2)。然而还是有点慢。

　　

　　我们发现，有一些区间的一些段的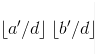是重复的，如下图。

　　

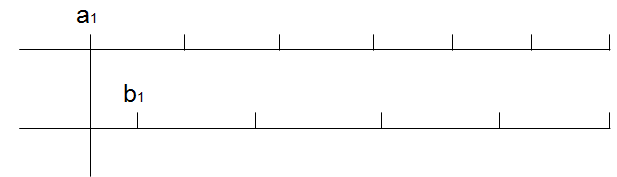
　　a1的意思是第一个使n/ai为整数的d。其他同理。

　　在（a1-1）之前的区间，我们发现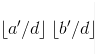一直是重复的，所以我们在线性筛里面放一个处理求Mobius函数的前缀和，最后把一些重复的直接用前缀和乘即可即可，这样节省了很多重复操作。

　　达到了O(nlogn)。

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>

#define viper 50005

using namespace std;

bool is_prime[viper];

int prime[viper],size=0,mu[viper],sum[viper];

void mu_choice()
{
    mu[1]=1;
    for(int i=2;i<=50000;i++)
    {
        if(!is_prime[i])prime[++size]=i,mu[i]=-1;
        int j=1,t=prime[j]*i;
        while(j<=size&&t<=50000)
        {
            is_prime[t]=1;
            if(i%prime[j]==0)
            {
                mu[t]=0;
                break;
            }
            else mu[t]=-mu[i];
            t=prime[++j]*i;
        }
    }
    for(int i=1;i<=50000;i++)sum[i]=sum[i-1]+mu[i];
}

int puck(int l,int r)
{
    if(l<r)swap(l,r);
    int last,re=0;
    for(int i=1;i<=r;i=last+1)
    {
        last=min(l/(l/i),r/(r/i));//每个重复区间的尾端
        re+=(sum[last]-sum[i-1])*(l/i)*(r/i);
    }
    return re;
}

int main()
{
    int T,a,b,c,d,k;
    mu_choice();
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
        a--,c--;
        a/=k,b/=k,c/=k,d/=k;
        printf("%d\n",puck(b,d)+puck(a,c)-puck(a,d)-puck(c,b));//容斥原理
    }
        return 0;
}

 

 

 

　　接下来我们来看下一题。。

　　BZOJ 2820 YY的GCD

 

 

Description

　　神犇YY虐完数论后给傻×kAc出了一题
　　给定N, M,求1<=x<=N, 1<=y<=M且gcd(x, y)为质数的(x, y)有多少对
　　kAc这种傻×必然不会了，于是向你来请教……
　　多组输入

Input

　　第一行一个整数T 表述数据组数
　　接下来T行，每行两个正整数，表示N, M

Output

　　T行，每行一个整数表示第i组数据的结果

Sample Input

　　2
　　10 10
　　100 100

Sample Output

　　30
　　2791

HINT

　　T = 10000
　　N, M <= 10000000

 

　　乍一看，这不和上题没什么区别啊。。不就是枚举质数然后随便求吗。。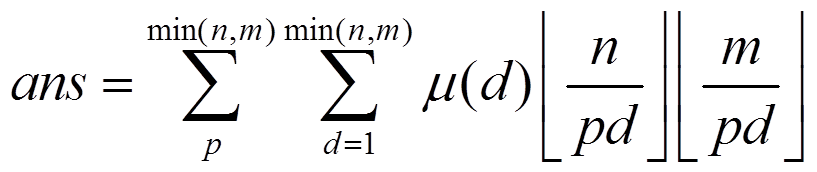

　　然而，这样求肯定TLE。。

　　让我们继续。

　　设T=pd，来变换一下。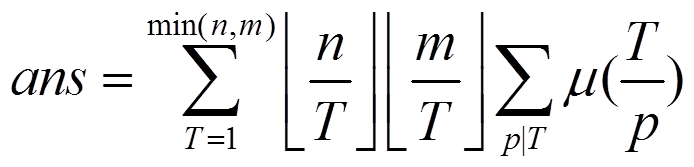

　　之后?把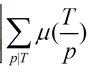预处理一下，把每个质数的倍数枚举一下，分块。。O（n）的时间复杂度(每个质数logn，n内一共n/logn个质数)。

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<cmath>
 4 #include<algorithm>
 5 
 6 #define N 10000001
 7 
 8 using namespace std;
 9 
10 int mu[N],prime[N],b=0;
11 long long f[N];
12 
13 bool is_prime[N];
14 
15 void get_mu()
16 {
17     mu[1]=1;
18     for(int i=2;i<=N-1;i++)
19     {
20         if(!is_prime[i])prime[++b]=i,mu[i]=-1;
21         int j=1,t=2*i;
22         while(j<=b&&t<=N-1)
23         {
24             is_prime[t]=1;
25             if(i%prime[j]==0)
26             {
27                 mu[t]=0;
28                 break;
29             }
30             mu[t]=-mu[i];
31             t=prime[++j]*i;
32         }
33     }
34     for(int i=1;i<=b;i++)
35     {
36         int p=prime[i];
37         for(int j=1;j*p<=N-1;j++)
38             f[p*j]+=mu[j];
39     }
40     for(int i=1;i<=N-1;i++)f[i]+=f[i-1];
41 }
42 
43 int main()
44 {
45     get_mu();
46     int T,l,r;
47     scanf("%d",&T);
48     while(T--) 
49     {
50         scanf("%d%d",&l,&r);
51         if(l<r)swap(l,r);
52         int last;
53         long long ans=0;
54         for(int i=1;i<=r;i=1+last)
55         {
56             last=min(l/(l/i),r/(r/i));
57             ans+=(long long)(f[last]-f[i-1])*(l/i)*(r/i);
58         }
59         printf("%lld\n",ans);
60     }
61     return 0;
62 }

 

 

 

　　BZOJ 3529 数表

　　

 　

Description

    有一张N×m的数表，其第i行第j列（1 < =i < =n，1 < =j < =m）的数值为
能同时整除i和j的所有自然数之和。给定a，计算数表中不大于a的数之和。

Input

    输入包含多组数据。
    输入的第一行一个整数Q表示测试点内的数据组数，接下来Q行，每行三个整数n，m，a(|a| < =10^9)描述一组数据。

Output

    对每组数据，输出一行一个整数，表示答案模2^31的值。

　　让我们先把这道题看简单一点(去掉a的限制)

　　求得是：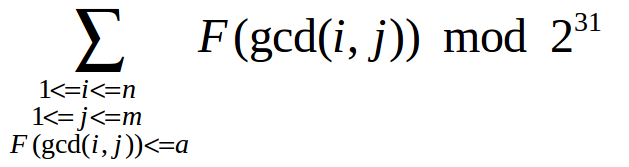

　　F(i)代表i的约数和。

　　

　　令g(i)为1<=x<=n,1<=y<=m,gcd(x,y)=i的数对(x,y)的个数

　　则有。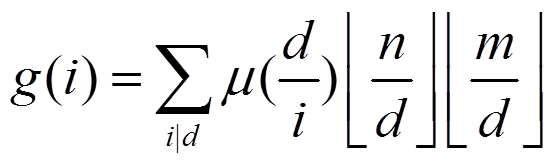

　　

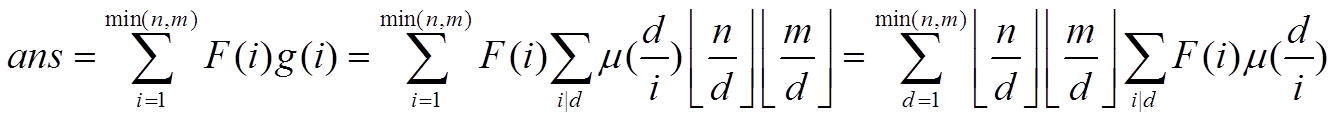
　　接下来又是喜闻乐见的前缀和。

　　在线性筛里面完成即可。

　　但是有a的限制，怎么办？

　　我们可以以a为关键字按升序排序，把F[i]按升序排序。

　　之后每次把a以内的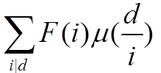按F[i]添加到一个树状数组里面，之后每次分块即可。。

　　

  1 #include<cstdio>
  2 #include<cstring>
  3 #include<cmath>
  4 #include<algorithm>
  5 
  6 #define maxq 40001
  7 
  8 #define maxn 100001
  9 
 10 using namespace std;
 11 
 12 struct ed{
 13     int a,n,m,id,ans;
 14 }a[maxq];
 15 
 16 bool is_prime[maxn];
 17 
 18 int prime[maxn],b=0,mu[maxn],bit[maxn],ans[maxn];
 19 
 20 struct sb{
 21     int num,Id;
 22 }f[maxn];
 23 
 24 void mu_choice()
 25 {
 26     mu[1]=1;
 27     for(int i=2;i<=maxn-1;i++)
 28     {
 29         if(!is_prime[i])prime[++b]=i,mu[i]=-1;
 30         int j=1,t=2*i;
 31         while(j<=b&&t<=maxn-1)
 32         {
 33             is_prime[t]=1;
 34             if(i%prime[j]==0)
 35             {
 36                 mu[t]=0;
 37                 break;
 38             }
 39             mu[t]=-mu[i];
 40             t=prime[++j]*i;
 41         }
 42     }
 43     for(int i=1;i<maxn;i++)
 44     {
 45         for(int j=1;j*i<maxn;j++)
 46             f[j*i].num+=i;
 47         f[i].Id=i;
 48     }
 49 }
 50 
 51 bool cmp(const ed A,const ed B)
 52 {
 53     return A.a<B.a;
 54 }
 55 
 56 bool cmp2(const sb A,const sb B)
 57 {
 58     return A.num<B.num;
 59 }
 60 
 61 void add(int pos,int num)
 62 {
 63     while(pos<=maxn-1)
 64     {
 65         bit[pos]+=num;
 66         pos+=pos&-pos;
 67     }
 68 }
 69 
 70 int sum(int pos)
 71 {
 72     int ne=0;
 73     while(pos>0)
 74     {
 75         ne+=bit[pos];
 76         pos-=pos&-pos;
 77     }
 78     return ne;
 79 }
 80 
 81 void solve(int x)
 82 {
 83     int last;
 84     for(int i=1;i<=a[x].n;i=last+1)
 85     {
 86         last=min(a[x].n/(a[x].n/i),a[x].m/(a[x].m/i));
 87         ans[a[x].id]+=(sum(last)-sum(i-1))*(a[x].n/i)*(a[x].m/i);
 88     }
 89 }
 90 
 91 int main()
 92 {
 93     #ifndef ONLINE_JUDGE
 94            freopen("3529.in","r",stdin);
 95           freopen("3529.out","w",stdout);
 96     #endif
 97     int T,aa,n,m;
 98     scanf("%d",&T);
 99     for(int i=1;i<=T;i++)
100     {
101         scanf("%d%d%d",&n,&m,&aa);
102         if(n>m)swap(n,m);
103         a[i].a=aa,a[i].n=n,a[i].m=m,a[i].id=i;
104     }
105     mu_choice();
106     sort(1+a,a+1+T,cmp);
107     sort(1+f,f+maxn,cmp2);
108     int puck=1;
109     for(int i=1;i<=T;i++)
110     {
111         while(puck<maxn&&f[puck].num<=a[i].a)
112         {
113             for(int j=1;j<=((maxn-1)/f[puck].Id);j++)
114                 add(j*f[puck].Id,mu[j]*f[puck].num);
115             puck++;
116         }
117         solve(i);
118     }
119     for(int i=1;i<=T;i++)
120         printf("%d\n",ans[i]&0x7fffffff);
121     return 0;
122 }
View Code

 

　　代码凑合着看吧。。　　

　　

　　

　　

　　

 

posted @ 2015-07-02 14:44  puck_just_me  阅读(343)  评论(0)  编辑  收藏  举报