组合数学学习笔记

组合计数学习笔记

By Tuifei_oier

前言

组合数学是在各省省选中经常会考到的一个知识点。
尤其会出现在各种颓式子算方案的题目当中。
为了避免被推式子所支配的恐惧，写下了这篇学习笔记，方便自己复习思考。

Part 1 组合恒等式

\(C_n^m=C_n^{n-m}\)
\(\sum\limits_{i=0}^nC_n^i=2^n\)
\(\sum\limits_{i=0}^nC_n^i [i\%2=0]=\sum\limits_{i=0}^nC_n^i [i\%2=1]=2^{n-1}\)
\(\sum\limits_{i=0}^mC_{n+i}^n=C_{n+m+1}^m\)
\(\sum\limits_{i=m}^nC_{i}^m=C_{n+1}^{m+1}\)
\(C_n^m\cdot C_m^k=C_n^k\cdot C_{n-k}^{m-k}\)
\(\sum_{i=0}^kC_n^i\cdot C_m^{k-i}=C_{n+m}^k\)
此式等价于上式\(\sum\limits_{i=0}\sum\limits_{j=0}C_n^i\cdot C_m^j\cdot[i\pm j=k]\)
(我相信自己以后能看得懂这些东西)

Part 2 自然数幂之和与斯特林数

设多项式 \(S_k(n)=\sum_{i=1}^ni^k\) ，则可以证明 \(S_k(n)\) 为关于 \(n\) 的 \(k+1\) 次多项式。
证明（归纳法+二项式定理）,自证不难。
(tips: \(\sum\limits_{i=1}^{n+1}((i+1)^{d+1}-i^{d+1})=?\))
证是证完了，我们咋求呢？

Met.1

拉格朗日插值求 \(S_k(n)\) 即可。
复杂度可以做到 \(O(k\log k)\) 具体做法详见拉格朗日插值。
但是这个算法是要求逆元的，所以它不适用于模数比较***钻的情况。所以，我们接下来会介绍一种复杂度不变，但是可以不必求逆元的算法。

Met.2

第一类斯特林数：\(i\) 个数分入 \(j\) 个非空环排列的方案数，记为 \(\begin{bmatrix}i\\j\end{bmatrix}\) 。
第二类斯特林数：\(i\) 个数分入 \(j\) 个非空集合的方案数，记为 \(\begin{Bmatrix}i\\j\end{Bmatrix}\) 。
递推公式：两类斯特林数均有递推公式。

\[\begin{bmatrix}i\\j\end{bmatrix}=\begin{bmatrix}i-1\\j-1\end{bmatrix}+(i-1)\begin{bmatrix}i-1\\j\end{bmatrix} \]

\[\begin{Bmatrix}i\\j\end{Bmatrix}=\begin{Bmatrix}i-1\\j-1\end{Bmatrix}+j\begin{Bmatrix}i-1\\j\end{Bmatrix} \]

\[\begin{bmatrix}i\\j\end{bmatrix}=\sum\limits_{k=1}^i\begin{bmatrix}i-k\\j-1\end{bmatrix}\times(k-1)!\times C_{i-1}^{k-1} \]

\[\begin{Bmatrix}i\\j\end{Bmatrix}=\sum\limits_{k=1}^i\begin{Bmatrix}i-k\\j-1\end{Bmatrix}\times C_{i-1}^{k-1} \]

这些递推公式可以通过组合意义来简单理解。
进一步，第二类斯特林数还有一个利用容斥理解的通项公式：

\[\begin{Bmatrix}i\\j\end{Bmatrix}=\dfrac{\sum\limits_{k=0}^j(-1)^kC_j^k(j-k)^i}{j!} \]

这个式子用到了一个常用技巧：通过乘上一个 \(j!\) 化无标号为了有标号（注意为什么可以这样做），这样一来就会方便很多，具体过程也可以用组合意义来理解。
但是这个东西的定义对我们解决自然数幂之和的问题有什么帮助呢？在后面讲完斯特林反演后你就会发现这个东西的妙用，它提供给我们一种复杂度 \(O(k^2)\) ，且模数随意的算法。

Met.3（扩展）

最后是一个生成函数相关的算法（伯努利数）。
先给出定义： \(\dfrac{x}{e^x-1}=\sum\limits_{i=0}^{+\infty}\dfrac{B_i}{i!}x^i\) 。
这就是神奇的伯努利数定义。
然后，通过一些神奇的操作，得出一个伯努利多项式：

\[\sum\limits_{i=0}^{+\infty}\dfrac{\beta_i(t)}{i!}x^i=\dfrac{x}{e^x-1}e^{tx} \]

这样一来，就可以得到：

\[\beta_n(t)=\sum\limits_{k=0}^nC_n^kB_{n-k}t^k \]

这就是伯努利多项式的通项公式，它的得来就是把二式右边的两数相乘用生成函数和一式拆开然后做卷积即可。
这个时候，有一个神奇的公式：

\[S_k(n)=\dfrac{1}{k+1}\sum\limits_{i=0}^kC_{k+1}^i(n+1)^iB_{k+1-i} \]

怎么来的？？
证明如下：首先构造一个这样的多项式：

\[\begin{matrix} \sum\limits_{i=0}^{+\infty}\dfrac{\beta_i(t+1)-\beta_i(t)}{i!}x^i=\\ \sum\limits_{i=0}^{+\infty}\dfrac{\beta_i(t+1)}{i!}x^i-\sum\limits_{i=0}^{+\infty}\dfrac{\beta_i(t)}{i!}x^i=\\ \dfrac{x}{e^x-1}e^{tx}(e^x-1)=\\ xe^{tx}=\\ x\sum\limits_{i=1}^{+\infty}\dfrac{t^i}{i!}x^i \end{matrix}\]

此时，左右都是关于 \(x\) 的多项式，考虑对应项系数：

\[\dfrac{\beta_{i+1}(t+1)-\beta_{i+1}(t)}{(i+1)!}=\dfrac{t^i}{i!} \]

\[t^i=\dfrac{\beta_{i+1}(t+1)-\beta_{i+1}(t)}{(i+1)} \]

这个时候就很显然该怎么做了（套个 \(\sum\)，然后右边用伯努利多项式通项公式化简）。
这样我们就可以 \(O(klogk)\) 的求出一个 \(S_k(n)\) 。
这里还有一点：怎么求 \(B\) ？在生成函数学习笔记中会有提到。

Part 3 容斥

谈到组合数学就离不开容斥这个玩意儿，毕竟它有相当广泛的用处，啥时候用都可以。
首先给出容斥定理：

\[|\cup_{i=1}^nA_i|=\sum\limits_{k=1}^n(-1)^{k+1}(\sum_{1\le i_1<i_2<...<i_k\le n}|A_{i_1}\cap A_{i_2}...\cap A_{i_k}|) \]

\[|\cap_{i=1}^nA_i|=\sum_{S\subset[n]}(-1)^{|S|}|\cap_{i\in S}C_UA_i| \]

这就是最基础的容斥定理，除此之外还有
min-max 容斥：

\[max{S}=\sum\limits_{T\subset S}(-1)^{|T|+1}min{T} \]

等其他推论。

min-max容斥的由来：
假设 \(S=\{1,3,4,7\}\) ,定义
\(A_1=\{1\},A_2=[1,3],A_3=[1,4],A_4=[1,7]\)
然后带入容斥定理的第一种形式中即可。

容斥的用法相当丰富，在后面的例题中在详解。

Part 4 斯特林数与斯特林反演

先是一些基础定义：

下降幂：\(x^{\underline{n}}=x(x-1)(x-2)...(x-n+1)\)
下降幂有一个简单性质：\(C_n^m\cdot m!=n^{\underline m}\)

上升幂：\(x^{\overline n}=x(x+1)(x+2)...(x+n-1)\)

接下来是两个定理：

\[x^k=\sum\limits_{i=0}^k\begin{Bmatrix}k\\i\end{Bmatrix}x^{\frac{i}{}} \]

\[x^{\overline{k}}=\sum\limits_{i=0}^k\begin{bmatrix}k\\i\end{bmatrix}x^i \]

第一个式子用组合意义很好理解，第二个式子可以用归纳法来证明（自证不难）。
然后就是重头戏了：斯特林反演。
先给出式子吧：

\[f(n)=\sum_{k=0}^n\begin{Bmatrix}n\\k\end{Bmatrix}g(k)\Longleftrightarrow g(n)=\sum_{k=0}^n(-1)^{n-k}\begin{bmatrix}n\\k\end{bmatrix}f(k) \]

接下来，我们要一步步推出斯特林反演。

Lemma.1

\[\begin{matrix}x^{\frac{n}{}}=(-1)^n(-x)^{\overline{n}} \\ x^{\overline{n}}=(-1)^n(-x)^{\frac{n}{}}\end{matrix} \]

这两个式子直接按定义拆开证明就好了。

Lemma.2

\[[m=n]=\sum_{k=m}^n(-1)^{n-k}\begin{bmatrix}n\\k\end{bmatrix}\begin{Bmatrix}k\\m\end{Bmatrix} \]

这个式子乍一看让人摸不着头脑，但是运用刚才的 Lemma.1 是可以证明(构造多项式)的：

\[\begin{matrix} n^m=\sum\limits_{i=0}^m\begin{Bmatrix}m\\i\end{Bmatrix}n^{\underline i} \\ =\sum\limits_{i=0}^m\begin{Bmatrix}m\\i\end{Bmatrix}(-1)^i(-n)^{\overline i} \\ \sum\limits_{i=0}^m\begin{Bmatrix}m\\i\end{Bmatrix}(-1)^i\sum\limits_{j=0}^i(-n)^j\begin{bmatrix}i\\j\end{bmatrix} \\ =\sum\limits_{j=0}^mn^j\sum\limits_{i=j}^m\begin{bmatrix}i\\j\end{bmatrix}\begin{Bmatrix}m\\i\end{Bmatrix} \end{matrix}\]

左右都是关于 \(n\) 的多项式，所以对应项系数相同。
所以 Lemma.2 得证。

最后，我们就可以运用 Lemma.2 直接代入证明斯特林反演了。

Extra?

还记得前文求自然幂之和的 Met.2 吗？我们现在就可以继续这个过程了。

首先，有一个下降幂的式子：

\[x^k=\sum\limits_{i=0}^k\begin{Bmatrix}k\\i\end{Bmatrix}x^{\frac{i}{}} \]

就别多想，套个斯特林反演。

\[x^{\underline k}=\sum_{i=0}^k(-1)^{k-i}\begin{bmatrix}k\\i\end{bmatrix}x^i \]

取出右边求和中的 \(x^k\) 一项，得：

\[x^k=x^{\underline k}-\sum_{i=0}^{k-1}(-1)^{k-i}\begin{bmatrix}k\\i\end{bmatrix}x^i \]

这个时候，使用我们的惯用套路：套 \(\sum\) ！

\[\begin{matrix} S_k(n)=\sum\limits_{x=1}^nx^k\\ =\sum\limits_{x=1}^n(x^{\underline k}-\sum\limits_{i=0}^{k-1}(-1)^{k-i}\begin{bmatrix}k\\i\end{bmatrix}x^i)\\ =k!\sum\limits_{x=1}^nC_x^k-\sum\limits_{x=1}^n\sum\limits_{i=0}^{k-1}(-1)^{k-i}\begin{bmatrix}k\\i\end{bmatrix}x^i \\ =k!C_{n+1}^{k+1}-\sum\limits_{i=0}^{k-1}(-1)^{k-i}\begin{bmatrix}k\\i\end{bmatrix}S_i(n) \end{matrix}\]

这样就得出了一个可以递推求出所有 \(S_k(n)\) 的算法了。

Part 5 Burnside Lemma

设 \(G\) 是作用于集合 \(S\) 的一个置换群，\(X^g\) 为一个 \(g\in G\) 作用于 \(S\) 时的不动点，\(|X/G|\) 为轨道数，则：

\[|X/G|=\dfrac{1}{|G|}\sum_{g\in G}|X^g| \]

这个式子中有很多奇怪的概念，在 OI 中我们通常可以这样理解：

置换

OI 中一般是类似旋转、翻转的操作，例如：
对于一个排列 \(p\)，我们把一个序列的 \(i\) 变为 \(p_i\) 的操作就是对原序列的一个置换。当 \(p=2,4,1,3\) 作用在序列 \(3,4,5,1,2\) 时，会得到：\(1,3,5,2,4\)。(\(1\rightarrow2,2\rightarrow4,3\rightarrow1,4\rightarrow3\))

对于一个集合而言，置换可以理解为从 \(S\) 到 \(S\) 本身的一个双射（一一对应）。

群

若干个元素组成的集合 \(G\)，需满足：

1. 包含单位元。即 \(\exists\ e\in G\) 满足 \(\forall\ g\in G\) 有 \(e\cdot g=g\cdot e=g\)。
2. 任意元素存在逆元。即 \(\forall\ x\in G,\exists\ y\in G\) 满足 \(x\cdot y=e\)。
3. 封闭性。即 \(\forall\ x,y\in G,x\cdot y\in G\)。
4. 结合律。即 \(a\cdot(b\cdot c)=(a\cdot b)\cdot c\)。

不动点

即当置换 \(g\) 作用于 \(S\) 时，如果 \(S\) 不发生本质上的改变，则将所有这样 \(S\) 组成的集合称为置换 \(g\) 的不动点。

轨道数

可以理解为在 \(G\) 中所有元素的作用下本质不同的点的个数。

通过一道题目来理解这些内容。

Part 6 例题

接下来就是检验前面学习的种种内容的时间了。

无向环染色

给定一个 \(n\) 个点的无标号环，用 \(m\) 种颜色给每个点染色，求染色方案数。
\(tips:1\le n,m\le10^9\)。

把环看成有标号，则我们相当于要知道有多少中本质不同的染色方案，两种方案如果可以通过旋转环上的点来相互得到就是本质相同。
考虑套用 Burnside 引理：

\[|X/G|=\dfrac{1}{|G|}\sum_{g\in G}|X^g| \]

则 \(S\) 就是有标号情况下所有 \(m^n\) 种染色方案构成的集合，\(G\) 就是一共 \(n\) 种旋转方式（顺时针转 \(1\) 个位置、\(2\) 个...\(n\) 个位置这 \(n\) 种方式（必须确保有单位元，即转 \(n\) 个位置））构成的集合，而 \(|X^g|\) 就是求有多少种 \(S\) 中的方案使得其转了 \(g\) 代表的位置后和原来相同，\(|X/G|\) 即为要求的答案。

于是：

\[ANS=\dfrac{1}{n}\sum_{i=1}^nf(i) \]

即枚举转 \(i\) 个位置，\(f(i)\) 为转 \(i\) 个位置后和原来相同的染色方案数。
考虑把旋转转化为一个作用于序列 \(1,2,3,...,n\) 的排列 \(p\)，即：

\[p=i,i+1,...,n,1,...,i-1 \]

如果我们建立一张 \(n\) 个点的图，\(i\) 向 \(p_i\) 连一条有向边，会得到若干个环，则称这些环就是置换 \(p\) 拆分成的轮换。
对于这道题的旋转，可以证明它会被拆分成 \((i,n)\) 个大小都为 \(\dfrac{n}{(i,n)}\) 的轮换。而不动点中元素需满足同一个轮换中的点染成同样的颜色，所以

\[f(i)=m^{(i,n)} \]

代回原式化简求值即可，复杂度 \(O(\log n)\)。

回文数个数

题意：给定 \(n\) ，询问有多少个 \(n\) 位数字串是回文的，且它的奇数位数字等于偶数位数字（可含前导 0 ）。
\(tips:n \le 10^6\)

三维偏序(加强？)

给定三个 \(n\) 的排列 \(A,B,C\) ，求满足 \(A_i<A_j,B_i<B_j,C_i<C_j\) 的点对 \((i,j)\) 数量。
\(tips:n\le10^6\)

子集族数量(ARC096E)

求有多少个子集族（可以简单理解为子集的集合），满足：

• 其中任意一个子集都是 \(\{1,2,...,n\}\) 的子集；
• 任意两个子集互不相同；
• \(1,2,...,n\) 都在其中至少出现了两次。

答案对 \(P\) 取模。
\(tips:2\le n\le3000,10^8\le P\le10^9+7,P\) 为质数。

方阵

给定 \(n\cdot m\) 的矩阵，每个格子填上 \([1,c]\) 中的数字，求任意两行都不相同且任意两列都不相同的方案数。
\(tips:n,m\le5000\)

连通块个数

求所有 \(n\) 个点的带标号无向图中的连通块个数的 \(k\) 次方之和。
\(tips:n\le10^5,k\le15,T\le10^5\)

求和(LOJ 2058)

给定 \(n\) ，求：

\[f(n)=\sum_{i=0}^n\sum_{j=0}^i\begin{Bmatrix}i\\j\end{Bmatrix}2^jj! \]

\(tips:1\le n\le10^5\)

建筑师(Luogu 4609)

求有多少个长度为 \(n\) 的排列 \(p\) 满足：从 \(1\) 到 \(n\) 将 \(p_i\) 入单调上升的不弹栈单调栈得到的栈大小为 \(x\)，从 \(n\) 到 \(1\) 将 \(p_i\) 入单调上升的不弹栈单调栈得到的栈大小为 \(y\)。
\(T\) 组询问。
\(tips:1\le n\le50000,1\le x,y\le100,1\le T\le2000\)

JZPTREE

给定一棵 \(n\) 个节点边权为 \(1\) 的树，要求对于每个点，求：

\[\sum_{j=1}^ndis(i,j)^m \]

\(tips:1\le n\le50000,1\le m\le500\)

Xor(SRM 670)

给定 \(m\) 张 \(n\) 个点的无向图，定义两个无向图的 \(xor\) 运算为：得到一个 \(n\) 个点的无向图，同时仅保留在两张图中总共出现恰好一次的边。
求有多少种方案在选出若干张无向图后，异或所得的图连通。
\(tips:1\le n\le9,1\le m\le50\)

小 c 的岛屿-Part 1

求 \(n\) 个点 \(m\) 条边的无向连通图数量。
\(tips:1\le n\le50\)

随机游走(Luogu 5643)

给定一棵 \(n\) 个点的树和一个起点 \(x\)，需回答 \(m\) 次询问：
每次询问给出一个 \([n]\) 的子集 \(S\)，回答从 \(x\) 开始在树上随机游走，期望需要走多少步才能到达 \(S\) 中的所有点。
定义随机游走：每次在所有与当前点有连边的点中等概率挑一个点走过去。
\(tips:1\le n\le18,1\le m\le5000\)

Part 7 例题题解

回文数个数

首先考虑 \(n\) 是偶数，则任意一个回文数字串都是满足条件的。
接下来只要考虑 \(n\) 为奇数的情况，分两种情况考虑：

1. \(n=4k+1\) ，此时最中间的位置是一个奇数位，我们写出题设条件的式子：
   \(2(a_1+a_3+...+a_{2k-1})+a_{2k+1}=2(a_2+a_4+...+a_{2k})\)
   两边除以 \(2\) ，则：
   \(a_1+a_3+...+a_{2k-1}+\dfrac{1}{2}a_{2k+1}=a_2+a_4+...+a_{2k}\)
   这时，我们再移项处理一下：
   \(a_1+a_3+...+a_{2k-1}-a_2-a_4-...-a_{2k}=-\dfrac{1}{2}a_{2k+1}\)
   注意到所有 \(a\in[0,9]\) ，则 \(-a\in[-9,0]\) ，所以 \(9-a\in[0,9]\) 。
   设 \(b_i=9-a_i\) ，有：
   \(a_1+a_3+...+a_{2k-1}+b_2+b_4+...+b_{2k}=9k-\dfrac{1}{2}a_{2k+1}\)
   这个时候左边所有数都是属于 \([0,9]\) 的，而右边可以通过枚举 \(a_{2k+1}\) 来变成一个常数，那么我们就只要考虑这样一个经典问题了：
   给定 \(n\) 个变量属于 \([0,x]\) ，且变量之和为 \(y\) ，求方案数。
   这个问题使用容斥+插板法就可以方便的解决了。
2. \(n=4k+3\) ，此时我们只要枚举前后两端的值，中间就又变成 \(n=4k+1\) 的情况了。

综上，复杂度为 \(O(n)\) ，不考虑组合数的预处理复杂度。

三维偏序加强版

因为 \(n\) 最大到 \(10^6\) ，所以 CDQ 啥的做法都会被卡。
但是有一个条件：\(A,B,C\) 都是排列，即限定值域且没有重复，所以可以从这里入手思考。
设 \(S_a\) 表示满足 \(A_i<A_j\) 的 \((i,j)\) 集合，\(S_b\) 表示满足 \(B_i<B_j\) 的 \((i,j)\) 集合，\(S_c\) 表示满足 \(C_i<C_j\) 的 \((i,j)\) 集合。则所求答案为 \(|S_a\cap S_b\cap S_c|\) 。
考虑用容斥来求，移项一下可得：

\[|S_a\cap S_b|+|S_a\cap S_c|+|S_b\cap S_c|-|S_a|-|S_b|-|S_c|+|U|=|S_a\cap S_b\cap S_c|+|C_{U}(S_a\cup S_b\cup S_c)| \]

其中不难发现 \(|C_{U}(S_a\cup S_b\cup S_c)|\) 恰等于 \(|S_a\cap S_b\cap S_c|\) ，而左边的东西都可以 \(O(nlogn)\) 的求值，所以总的复杂度为 \(O(nlogn)\) 。

ARC 096E

题目中的“至少出现 \(2\) 次”给我们启发，让我们有了尝试容斥的想法。
设 \(f(i)\) 表示至少有 \(i\) 个数字出现次数 \(\le1\) 的方案数，则答案为：

\[\sum_{i=0}^n(-1)^iC_n^if(i) \]

考虑 \(f(i)\) 的求法。因为有 \(i\) 个数字出现了 \(\le1\) 次，我们就先确定要把这个 \(i\) 个出现次数 \(\le1\) 的数字分入 \(j\) 个集合。
但是这时就会有一个问题：可能有的数字没有出现过，这个时候怎么办？
一种比较巧妙的解决方法是新加入一个集合，其中有一个元素 \(0\) ，然后 \(i\) 个数字分入 \(j+1\) 个集合，和 \(0\) 在一个集合的就是没出现过，那么方案数为 \(\begin{Bmatrix}i+1\\j+1\end{Bmatrix}\) 。
接下来就考虑剩下的 \(n-i\) 个数字随便放，所以

\[f(i)=\sum_{j=0}^i\begin{Bmatrix}i+1\\j+1\end{Bmatrix}2^{2^{n-i}}2^{(n-i)j} \]

所以最终答案为：

\[\sum_{i=0}^n(-1)^iC_n^i\sum_{j=0}^i\begin{Bmatrix}i+1\\j+1\end{Bmatrix}2^{2^{n-i}}2^{(n-i)j} \]

复杂度 \(O(n^2)\)。

方阵

这道题首先可以只考虑 \(n\) 行 \(m\) 列的方格每一行都不相同的方案数，记为 \(f(m)\)，则：

\[f(m)=(c^m)^{\underline n} \]

之后，考虑怎么求每行每列都不相同的方案数，记为 \(g(m)\)。发现这个东西不是很好直接求。
这时，我们可以考虑反演来得出它的值：
首先，考虑用 \(g(m)\) 来表示 \(f(m)\) ：

\[f(m)=\sum_{i=0}^m\begin{Bmatrix}m\\i\end{Bmatrix}g(i) \]

这个式子的意思是：把这 \(m\) 列分成 \(i\) 种类型，然后每种类型各不相同。
这个时候套斯特林反演，得到：

\[g(m)=\sum_{i=0}^m(-1)^{m-i}\begin{bmatrix}m\\i\end{bmatrix}f(i) \]

于是就可以 \(O(nm)\) 的解决这个问题了。

连通块个数

考虑一个这样的式子(重点！！)：

\[(\sum_{i=1}^nx_i)^m=\sum_{j=0}^m\begin{Bmatrix}m\\j\end{Bmatrix}j!C_{\sum_{i=1}^nx_i}^j \]

如果 \(x_i\in\{0,1\}\)，则这个式子可以理解为：对于一个状态 \(\{x_1,x_2,...,x_n\}\)，如果它其中的 \(j\) 个 \(x_i\) 同时为 \(1\)，则会对答案产生 \(\begin{Bmatrix}m\\j\end{Bmatrix}j!\) 的贡献。
在这样的基础上，我们来考虑这道题。
设 \(x_i\) 表示第 \(i\) 种连通块是否出现，我们可以把答案写成：

\[\sum_G(\sum x_i)^k \]

即

\[\sum_G\sum_{j=0}^k\begin{Bmatrix}k\\j\end{Bmatrix}j!C_{\sum x_i}^j \]

\[=\sum_{j=0}^k\begin{Bmatrix}k\\j\end{Bmatrix}j!\sum_GC_{\sum x_i}^j \]

我们只要求 \(\sum\limits_GC_{\sum x_i}^j\)，即有多少种情况同时有 \(j\) 个选定的 \(x_i\) 为 \(1\) ，即等价于 \(\sum\limits_{|S|=j}cnt(S)\)，\(cnt(S)\) 为包含 \(S\) 中连通块的 \(n\) 个点的图数量。
考虑如何求这个，我们设 \(g_{i,j}\) 表示 \(i\) 个点构成 \(j\) 个连通块的方案数，\(f_i\) 表示 \(i\) 个点连通图的数量，则：

\[g_{i,j}=\sum_{l=1}^iC_{i-1}^{l-1}f_l\,g_{i-l,j-1} \]

\[f_i=2^{C_i^2}-\sum_{j=1}^{i-1}C_{i-1}^{j-1}f_j\times2^{C_{i-j}^2} \]

则最终答案为：

\[\sum_{j=0}^k\begin{Bmatrix}k\\j\end{Bmatrix}j!\sum_{i=1}^nC_n^ig_{i,j}2^{C_{n-i}^2} \]

卷积求 \(f,g\) 后，每组询问也可以卷积求答案，复杂度 \(O((n+Tk)logn)\)。

求和

\[\begin{matrix} f(n)=\sum\limits_{i=0}^n\sum\limits_{j=0}^i\begin{Bmatrix}i\\j\end{Bmatrix}2^jj! \\ =\sum\limits_{j=0}^n2^j\sum\limits_{i=0}^n\begin{Bmatrix}i\\j\end{Bmatrix}j! \\ =\sum\limits_{j=0}^n2^j\sum\limits_{i=0}^n\sum\limits_{k=0}^j(-1)^kC_j^k(j-k)^i \\ =\sum\limits_{j=0}^n2^j\sum\limits_{k=0}^j(-1)^kC_j^k\sum\limits_{i=0}^n(j-k)^i \\ =\sum\limits_{j=0}^n2^j\sum\limits_{k=0}^j(-1)^kC_j^k\dfrac{(j-k)^{n+1}-1}{j-k-1} \end{matrix}\]

不难发现这个式子是可以卷积的，于是这道题就被解决了，复杂度 \(O(n\log n)\)。

建筑师

考虑在 \(n\) 出现位置的左边，有 \(x-1\) 个“可视”楼，右边有 \(y-1\) 个。
此时我们可以发现一个性质：一个将 \(n-1\) 个数分为 \(x+y-2\) 个圆排列的方案，恰好对应 \(C_{x+y-2}^{x-1}\) 个原题的合法方案。

考虑为什么这是对的，我们如果将除了 \(n\) 以外的 \(x+y-2\) 个可视楼分别把它们和因为它们而不可视的楼“打包在一起”，如图：

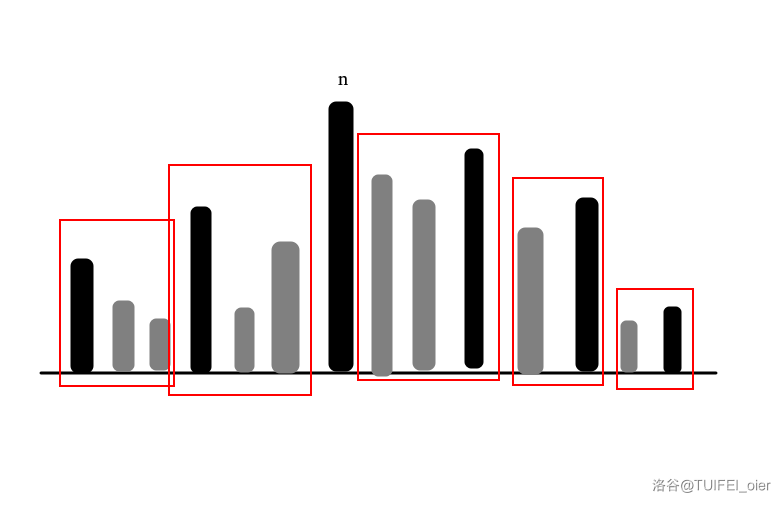
这样我们会得到 \(x+y-2\) 个包，且黑色的可视楼都是每个包内最高的楼。
因此，这 \(x+y-2\) 个包可以映射一个 \(n-1\) 个数 \(x+y-2\) 个圆排列的方案。
对于这 \(x+y-2\) 个包一共可以有 \(C_{x+y-2}^{x-1}\) 种分别放在 \(n\) 左右的方案，因此它们一起对应一种圆排列，这样就证明了：\(C_{x+y-2}^{x-1}\) 种原序列方案恰映射一种圆排列；

其次，考虑任何一个圆排列，我们也可以构造出 \(C_{x+y-2}^{x-1}\) 种原序列的方案，因此它们是一一对应的，于是本题答案即为：

\[\begin{bmatrix}n-1\\x+y-2\end{bmatrix}C_{x+y-2}^{x-1} \]

这种通过构造一一对应关系来转化题目的想法非常值得积累。

JZPTREE

考虑一个这样的式子：

\[x^k=\sum_{i=1}^k\begin{Bmatrix}k\\i\end{Bmatrix}x^{\frac{i}{}} \]

则答案可以转化为：

\[ANS_x=\sum_{y=1}^n(dis(x,y))^m \]

\[=\sum_{y=1}^n\sum_{i=1}^m\begin{Bmatrix}m\\i\end{Bmatrix}(dis(x,y))^{\frac{i}{}} \]

\[=\sum_{i=1}^m\begin{Bmatrix}m\\i\end{Bmatrix}\sum_{y=1}^n(dis(x,y))^{\frac{i}{}} \]

则我们可以考虑设状态 \(dp_{i,j}\) 表示 \(i\) 子树中的点到 \(i\) 的距离的 \(j\) 次下降幂的和，就可以 \(O(nm)\) 转移了。
这之后，换根 DP 出每个点的答案，代入计算即可。
复杂度 \(O(nm)\)。

随机游走

当 DP 的转移过程存在环时，我们有一个算法是通过高斯消元来解方程。
实际上，当 DP 的转移是在树上进行，且仅跟儿子和父亲有关时，我们有这样一个更优的解法：我们可以得出这样的方程：

\[f_x=A_xf_{fa}+B_x \]

即，我们可以把原本关于若干个 \(f\) 的方程，写成一个只跟 \(f_x,f_{fa}\) 相关，而其他项全部作为常量的形式。
这样一来，如果最后化出来的 \(A_x,B_x\) 都与父亲无关，我们就可以直接树形 DP 求出每个点的 \(A_x,B_x\)，之后 \(dp_{root}=B_{root}\)，然后就可以从上到下 \(O(n)\) 求解 \(f_x\) 了。

对于这道题，我们首先使用 \(min-max\) 容斥，然后在树上用这样的 idea 进行 DP（\(f_{x,S}\) 表示 \(x\) 点第一次碰到 \(S\) 中的点期望还需多少步），求出根节点的 DP 值然后就可以得出答案了。时间复杂度 \(O(Q2^n)\)。
事实上，如果预处理出对于每个 \(S\) 的 \(f_{root,S}\)，则我们可以用 FWT 求一个子集和，时间复杂度优化为 \(O(n2^n+Q)\)。

这个 idea 非常重要且比较简单，需要熟练掌握。

Summary

组合数学是 oi 数学中的主要考点，掌握它是学习 oi 数学相当重要的一方面。
通过两天的学习和做题，相信自己会对这个知识点有更深一步的理解。