代码改变世界

javascript数据结构与算法-- 二叉树

2015-03-23 21:22  龙恩0707  阅读(12427)  评论(10)  编辑  收藏  举报

javascript数据结构与算法-- 二叉树

  树是计算机科学中经常用到的一种数据结构。树是一种非线性的数据结构，以分成的方式存储数据，树被用来存储具有层级关系的数据，比如文件系统的文件，树还被用来存储有序列表。我们要研究的是二叉树，在二叉树上查找元素非常快，为二叉树添加元素或者删除元素，也是非常快的。

树的基本结构示意图如下：

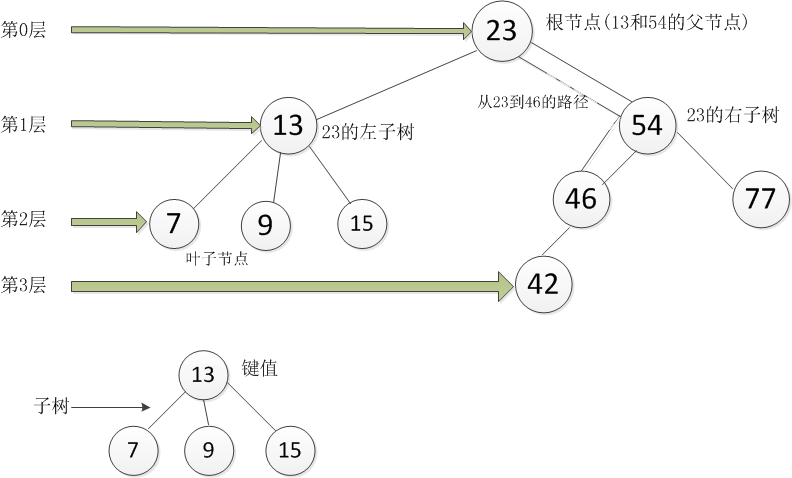
我们现在最主要的是要来学习二叉树，二叉树是一种特殊的树，它的特征是 子节点个数不超过2个。如下图就是二叉树的基本结构示意图如下：

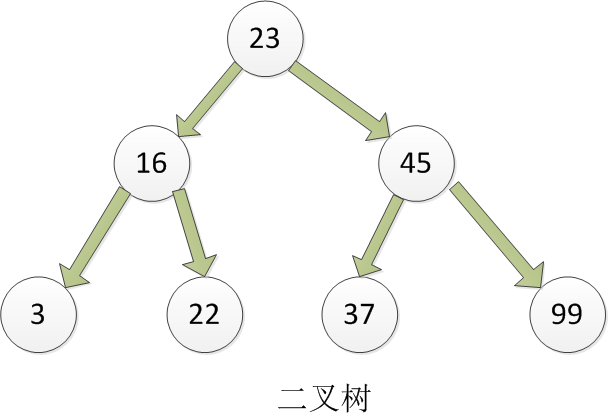
二叉树是一种特殊的树，相对较少的值保存在左节点上，较大的值保存在右节点中。这一特性使得查找的效率非常高，对于数值型和非数值型的数据，比如单词和字符串都是一样。

下面我们来学习插入节点的操作吧！

1.   二叉树是由节点组成的，所以我们需要定义一个对象node，可以保存数据，也可以保存其他节点的链接(left 和 right)，show()方法用来显示保存在节点中的数据。Node代码如下：

 function Node(data,left,right) {
    this.data = data;
    this.left = left;
    this.right = right;
    this.show = show;
}

插入节点分析如下：

代码如下：

function Node(data,left,right) {
    this.data = data;
    this.left = left;
    this.right = right;
    this.show = show;
}
function show() {
    return this.data;
}
function BST() {
    this.root = null;
    this.insert = insert;
    this.inOrder = inOrder;
}
function insert(data) {
    var n = new Node(data,null,null);
    if(this.root == null) {
        this.root = n;
    }else {
        var current = this.root;
        var parent;
        while(current) {
            parent = current;
            if(data <  current.data) {
                current = current.left;
                if(current == null) {
                    parent.left = n;
                    break;
                }
            }else {
                current = current.right;
                if(current == null) {
                    parent.right = n;
                    break;
                }
            }
        }
    }
}
初始代码如下：
var nums = new BST();
nums.insert(23);
nums.insert(45);
nums.insert(16);
nums.insert(37);
nums.insert(3);
nums.insert(99);
nums.insert(22);

示意图如下：

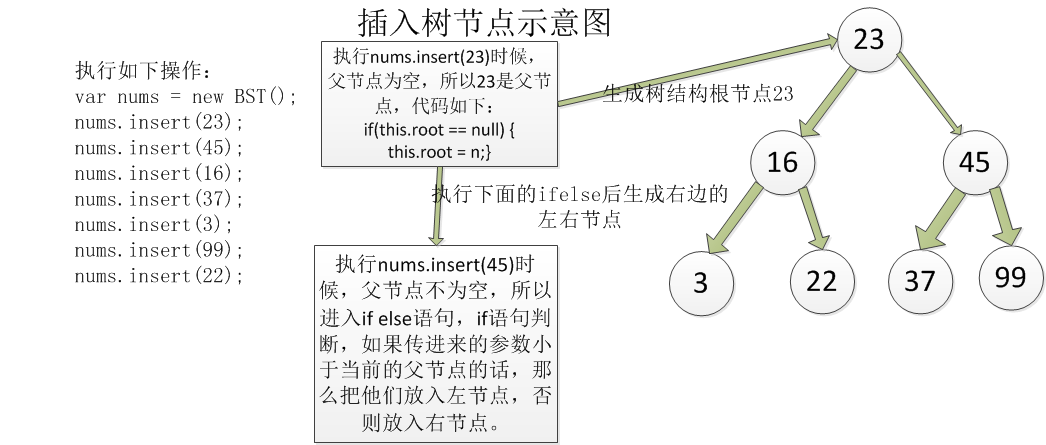
1. 执行insert(23)时候，由于根节点== null 所以 根节点为23.

2. 执行insert(45)的时候，根节点不等于null，因此进入while语句；由于45 > 大于根节点23 所以就进入else语句，当前current的值如下图：

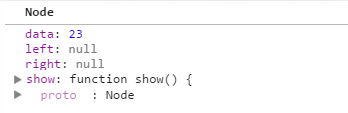
当执行 current = current.right; 这句代码时候，当前current值变为null了，然后进行if判断代码如下：

if(current == null) {
         parent.right = n;
         break;

}

所以45为根节点的右节点了。跳出循环语句；

3. 执行insert(16)的时候，根节点不等于null，因此进入while语句，由于16 < 小于根节点23，所以就进入if语句，那么当前的current值如下：

当执行到 current = current.left; 的时候，current的值就变为null，所以接着往下执行代码：

if(current == null) {
    parent.left = n;
    break;
}

就把当前的节点16插入到根节点的左节点上。

4. 接着执行 insert(37) 的时候，根节点不等于null，因此进入else语句中的while语句，由于37 大于根节点23，所以就进入while语句中的else语句，当前的current值为：

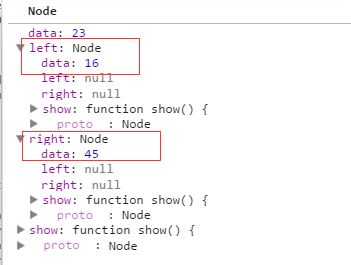
当执行current = current.right;这句代码的时候，那么当前current = 45的那个节点(如上图所示)；当再执行下面的代码：

if(current == null) {
    parent.right = n;
    break;
}

那么current != null 所以接着进入下一次while循环，执行这句代码后；parent = current;

那么parent = 45的那个节点了，current值如下所示：

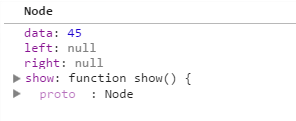
接着进入if语句判断，由于当前的根节点是45，所以37 小于根节点 45了，所以就进入if语句代码如下：

if(data <  current.data) {
    current = current.left;
    if(current == null) {
        parent.left = n;
        break;
    }
}

Current = current.left 因此current = null; 继续执行上面的if语句判断是否为null的时候，因此就把37放入根节点为45的左节点上了。

5. 直接执行insert(3); 的时候，根节点不为空，所以就进入else语句的while语句中，由于当前的data = 3，所以执行如下if判断代码：

if(data <  current.data) {
    current = current.left;
    if(current == null) {
        parent.left = n;
        break;
    }
}

插入的节点值3 小于 根节点23，进入if语句里面执行，但是当前的current值如下：

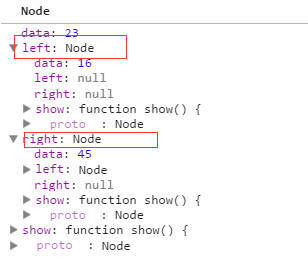
所以当执行 current = current.left 的时候，那么current = 16的那个节点了，如下所示：

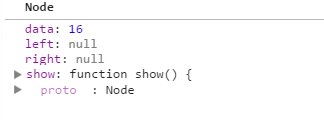
因此current 不等于null，所以就执行到下一次while循环，继续进入while中的if判断，由于当前的根节点是16，所以也就进入了if里面的代码去执行，在执行这句代码后：

current = current.left; 由上图可知：current = null；current就等于null了；再执行代码如下：

if(current == null) {
    parent.left = n;
    break;
}

就把节点3 插入到当前的根节点为16的左节点了。

6. 执行insert(99)的时候；当前的根节点23 小于 99，那么就进入else语句了，那么current值就等于如下：

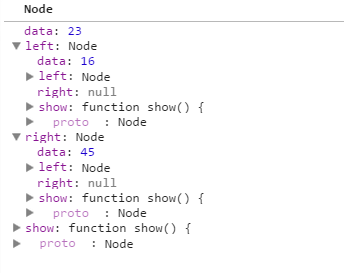
当执行 current = current.right; 的时候 ，那么current 就等于如下：

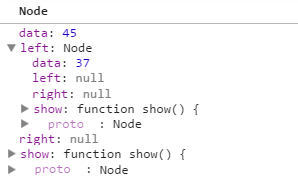
再接着执行代码：

if(current == null) {
    parent.right = n;
    break;
}

如上图所示，current并不等于null，所以执行下一次while循环，继续进入while中的else语句，那么当前的current值如下：

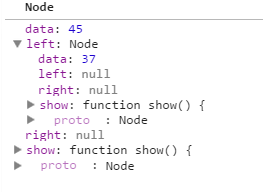
当执行current = current.right;这句代码的时候，那么current 就等于 null了，所以执行if语句代码如下：

if(current == null) {
    parent.right = n;
    break;
}

就把99节点插入到当前的根节点为45节点的右节点了。

7. 执行 insert(22);的时候，由于根节点为23，所以节点22 小于 23，所以进入while中的if语句里面了，那么当前current值如下：

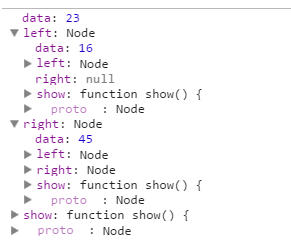
当执行 current = current.left; 的时候，那么current值变为如下所示：

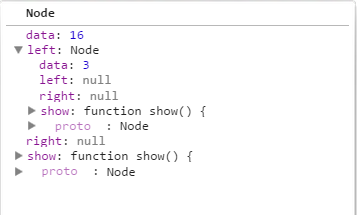
所以执行 if语句代码如下：

if(current == null) {
    parent.left = n;
    break;
}

不等于null，所以斤进入while下一次循环，由于当前的根节点16 小于插入的节点22 ，所以就进入else语句了，那么当前的current值如下：

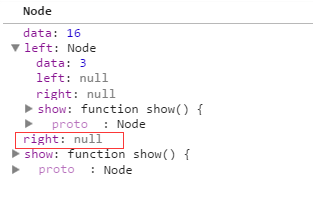
再执行这句代码 current = current.right; 那么current就等于null了；因此就把节点22插入到根节点为16上面的右节点上了；

以上是插入节点的整个流程！

二：遍历二叉查找树；

遍历二叉树的方法有三种，中序，先序和后序。

1. 中序；

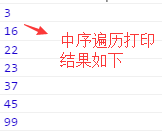
如下图所示：

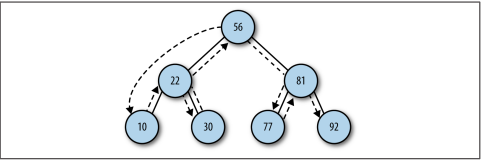
中序遍历使用递归的方式实现，该方法需要以升序访问树中的所有节点，先访问左子树，再访问根节点，最后访问右子树。

代码如下：

// 中序遍历
function inOrder(node) {
       if(!(node == null)) {
           inOrder(node.left);
           console.log(node.show());
           inOrder(node.right);
       }
}

代码分析如下：

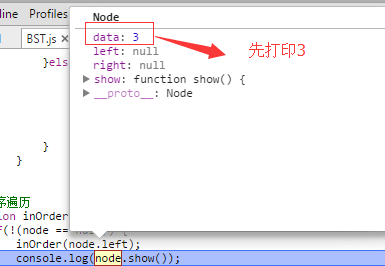
JS所有代码如下：

function Node(data,left,right) {
    this.data = data;
    this.left = left;
    this.right = right;
    this.show = show;
}

function show() {
    return this.data;
}

function BST() {
    this.root = null;
    this.insert = insert;
    this.inOrder = inOrder;
}

function insert(data) {
    var n = new Node(data,null,null);
    if(this.root == null) {
        this.root = n;
    }else {
        var current = this.root;
        var parent;
        while(current) {
            parent = current;
            if(data <  current.data) {
                current = current.left;
                if(current == null) {
                    parent.left = n;
                    break;
                }
            }else {
                current = current.right;
                if(current == null) {
                    parent.right = n;
                    break;
                }
            }
        }
    }
}
// 中序遍历
function inOrder(node) {
    if(!(node == null)) {
        inOrder(node.left);
        console.log(node.show());
        inOrder(node.right);
    }
}
代码初始化如下：
var nums = new BST();
nums.insert(23);
nums.insert(45);
nums.insert(16);
nums.insert(37);
nums.insert(3);
nums.insert(99);
nums.insert(22);
inOrder(nums.root);

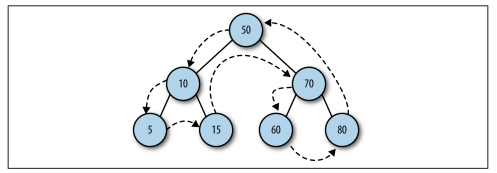
2. 先序：先序遍历先访问根节点，然后以同样方式访问左子树和右子树。如下图所示：

代码如下：

// 先序遍历 
function preOrder(node) {
       if(!(node == null)) {
           console.log(node.show());
           preOrder(node.left);
           preOrder(node.right);
        }
}

JS所有代码如下：

function Node(data,left,right) {
    this.data = data;
    this.left = left;
    this.right = right;
    this.show = show;
}
function show() {
    return this.data;
}
function BST() {
    this.root = null;
    this.insert = insert;
    this.inOrder = inOrder;
}
function insert(data) {
    var n = new Node(data,null,null);
    if(this.root == null) {
        this.root = n;
    }else {
        var current = this.root;
        var parent;
        while(current) {
            parent = current;
            if(data <  current.data) {
                current = current.left;
                if(current == null) {
                    parent.left = n;
                    break;
                }
            }else {
                current = current.right;
                if(current == null) {
                    parent.right = n;
                    break;
                }
            }
        }
    }
}
// 中序遍历
function inOrder(node) {
    if(!(node == null)) {
        inOrder(node.left);
        console.log(node.show());
        inOrder(node.right);
    }
}

// 先序遍历 
function preOrder(node) {
    if(!(node == null)) {
        console.log(node.show());
        preOrder(node.left);
        preOrder(node.right);
    }
}
初始化代码如下：
var nums = new BST();
nums.insert(23);
nums.insert(45);
nums.insert(16);
nums.insert(37);
nums.insert(3);
nums.insert(99);
nums.insert(22);
console.log("--------------");
preOrder(nums.root);

先序遍历打印如下：

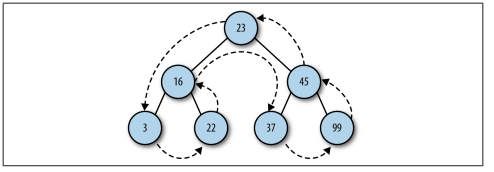
3. 后序：后序遍历先访问叶子节点，从左子树到右子树，再到根节点，如下所示：

JS代码如下：

// 后序遍历
function postOrder(node) {
    if(!(node == null)) {
        postOrder(node.left);
        postOrder(node.right);
        console.log("后序遍历"+node.show());
    }
}

所有的JS代码如下：

function Node(data,left,right) {
    this.data = data;
    this.left = left;
    this.right = right;
    this.show = show;
}

function show() {
    return this.data;
}

function BST() {
    this.root = null;
    this.insert = insert;
    this.inOrder = inOrder;
}

function insert(data) {
    var n = new Node(data,null,null);
    if(this.root == null) {
        this.root = n;
    }else {
        var current = this.root;
        var parent;
        while(current) {
            parent = current;
            if(data <  current.data) {
                current = current.left;
                if(current == null) {
                    parent.left = n;
                    break;
                }
            }else {
                current = current.right;
                if(current == null) {
                    parent.right = n;
                    break;
                }
            }
        }
    }
}
// 中序遍历
function inOrder(node) {
    if(!(node == null)) {
        inOrder(node.left);
        console.log(node.show());
        inOrder(node.right);
    }
}

// 先序遍历 
function preOrder(node) {
    if(!(node == null)) {
        console.log(node.show());
        preOrder(node.left);
        preOrder(node.right);
    }
}

// 后序遍历
function postOrder(node) {
    if(!(node == null)) {
        postOrder(node.left);
        postOrder(node.right);
        console.log("后序遍历"+node.show());
    }
}
页面初始化如下：
var nums = new BST();
nums.insert(23);
nums.insert(45);
nums.insert(16);
nums.insert(37);
nums.insert(3);
nums.insert(99);
nums.insert(22);
console.log("--------------");
postOrder(nums.root);

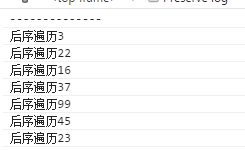
打印如下：

在二叉查找树上进行查找

查找二叉树上的最小值与最大值非常简单，因为较小的值总是在左子节点上，在二叉树上查找最小值，只需要遍历左子树，直到找到最后一个节点。

1. 二叉树查找最小值

代码如下：

// 二叉树查找最小值
function getMin(){
    var current = this.root;
    while(!(current.left == null)) {
         current = current.left;
      }
    return current.data;
}

所有JS代码如下：

function Node(data,left,right) {
    this.data = data;
    this.left = left;
    this.right = right;
    this.show = show;
}

function show() {
    return this.data;
}

function BST() {
    this.root = null;
    this.insert = insert;
    this.inOrder = inOrder;
    this.getMin = getMin;
}

function insert(data) {
    var n = new Node(data,null,null);
    if(this.root == null) {
        this.root = n;
    }else {
        var current = this.root;
        var parent;
        while(current) {
            parent = current;
            if(data <  current.data) {
                current = current.left;
                if(current == null) {
                    parent.left = n;
                    break;
                }
            }else {
                current = current.right;
                if(current == null) {
                    parent.right = n;
                    break;
                }
            }
        }
    }
}
// 中序遍历
function inOrder(node) {
    if(!(node == null)) {
        inOrder(node.left);
        console.log(node.show());
        inOrder(node.right);
    }
}

// 先序遍历 
function preOrder(node) {
    if(!(node == null)) {
        console.log(node.show());
        preOrder(node.left);
        preOrder(node.right);
    }
}

// 后序遍历
function postOrder(node) {
    if(!(node == null)) {
        postOrder(node.left);
        postOrder(node.right);
        console.log("后序遍历"+node.show());
    }
}

// 二叉树查找最小值
function getMin(){
    var current = this.root;
    while(!(current.left == null)) {
        current = current.left;
    }
    return current.data;
}
测试代码初始化如下：
var nums = new BST();
nums.insert(23);
nums.insert(45);
nums.insert(16);
nums.insert(37);
nums.insert(3);
nums.insert(99);
nums.insert(22);
var min = nums.getMin();
console.log(min);  // 打印出3

代码分析如下：

1 当执行到getMin()方法内的 var current = this.root的时候，当前的this.root的值为如下：

 

因此进入while内的循环，执行到代码：

current = current.left，current.left值如下：

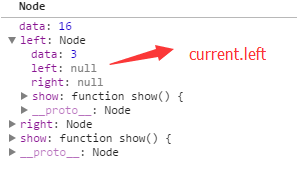
赋值给current，因此current等于上面的节点。接着继续循环遍历while，执行到代码 current = current.left ， current.left值变成如下：

然后值赋值给current。再继续遍历，进入while循环，while(!(current.left == null)) {}代码判断，由上图可知；current.left = null,因此就跳出整个while循环，因此打印3出来。

2.在二叉树上查找最大值；只需遍历右子树，直到查到最后一个节点，该节点上保存的值即为最大值。

JS代码如下：

// 二叉树上查找最大值
function getMax() {
    var current = this.root;
    while(!(current.right == null)) {
        current = current.right;
    }
    return current.data;
}

下面是所有的JS代码：

function Node(data,left,right) {
    this.data = data;
    this.left = left;
    this.right = right;
    this.show = show;
}

function show() {
    return this.data;
}

function BST() {
    this.root = null;
    this.insert = insert;
    this.inOrder = inOrder;
    this.getMin = getMin;
    this.getMax = getMax;
}

function insert(data) {
    var n = new Node(data,null,null);
    if(this.root == null) {
        this.root = n;
    }else {
        var current = this.root;
        var parent;
        while(current) {
            parent = current;
            if(data <  current.data) {
                current = current.left;
                if(current == null) {
                    parent.left = n;
                    break;
                }
            }else {
                current = current.right;
                if(current == null) {
                    parent.right = n;
                    break;
                }
            }
        }
    }
}
// 中序遍历
function inOrder(node) {
    if(!(node == null)) {
        inOrder(node.left);
        console.log(node.show());
        inOrder(node.right);
    }
}

// 先序遍历 
function preOrder(node) {
    if(!(node == null)) {
        console.log(node.show());
        preOrder(node.left);
        preOrder(node.right);
    }
}

// 后序遍历
function postOrder(node) {
    if(!(node == null)) {
        postOrder(node.left);
        postOrder(node.right);
        console.log("后序遍历"+node.show());
    }
}

// 二叉树查找最小值
function getMin(){
    var current = this.root;
    while(!(current.left == null)) {
        current = current.left;
    }
    return current.data;
}

// 二叉树上查找最大值
function getMax() {
    var current = this.root;
    while(!(current.right == null)) {
        current = current.right;
    }
    return current.data;
}
HTML初始化如下：
var nums = new BST();
nums.insert(23);
nums.insert(45);
nums.insert(16);
nums.insert(37);
nums.insert(3);
nums.insert(99);
nums.insert(22);
var min = nums.getMin();
console.log(min);

var max = nums.getMax();
console.log(max);

分析还是和上面最小值分析一个道理，这里就不分析了。

上面2个方法返回最小值和最大值，但是有时候，我们希望方法返回存储最小值和最大值的节点，这很好实现，只需要修改方法，让它返回当前节点，而不是节点中存储的数据即可。

在二叉树上查找给定值

 在二叉树上查找给定值，需要比较该值和当前节点上的值得大小。通过比较，就能确定如果给定值不在当前节点时，就要向左遍历和向右遍历了。

代码如下：

// 查找给定值
function find(data) {
    var current = this.root;
    while(current != null) {
        if(current.data == data) {
            return current;
        }else if(data < current.data) {
            current = current.left;
        }else {
            current = current.right;
        }
    }
    return null;
}

代码分析如下：

比如现在的二叉树是如下这个样子：

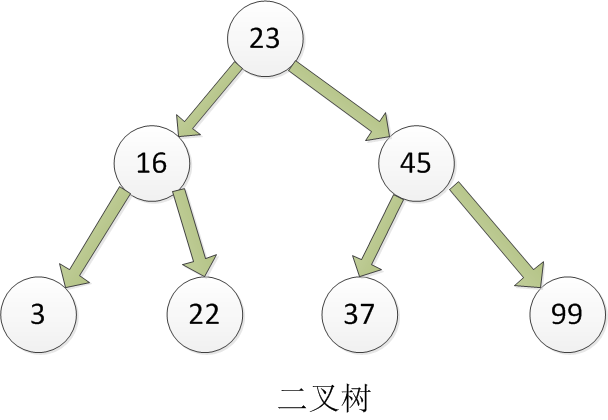
页面初始化 查找二叉树上的45 节点，代码初始化如下：

var value = nums.find("45");

截图如下：

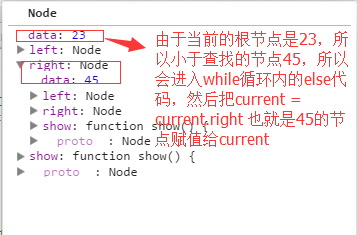
然后就return 45的节点上了。

所有的JS代码如下：

function Node(data,left,right) {
    this.data = data;
    this.left = left;
    this.right = right;
    this.show = show;
}

function show() {
    return this.data;
}

function BST() {
    this.root = null;
    this.insert = insert;
    this.inOrder = inOrder;
    this.getMin = getMin;
    this.getMax = getMax;
    this.find = find;
}

function insert(data) {
    var n = new Node(data,null,null);
    if(this.root == null) {
        this.root = n;
    }else {
        var current = this.root;
        var parent;
        while(current) {
            parent = current;
            if(data <  current.data) {
                current = current.left;
                if(current == null) {
                    parent.left = n;
                    break;
                }
            }else {
                current = current.right;
                if(current == null) {
                    parent.right = n;
                    break;
                }
            }
        }
    }
}
// 中序遍历
function inOrder(node) {
    if(!(node == null)) {
        inOrder(node.left);
        console.log(node.show());
        inOrder(node.right);
    }
}

// 先序遍历 
function preOrder(node) {
    if(!(node == null)) {
        console.log(node.show());
        preOrder(node.left);
        preOrder(node.right);
    }
}

// 后序遍历
function postOrder(node) {
    if(!(node == null)) {
        postOrder(node.left);
        postOrder(node.right);
        console.log("后序遍历"+node.show());
    }
}

// 二叉树查找最小值
function getMin(){
    var current = this.root;
    while(!(current.left == null)) {
        current = current.left;
    }
    return current.data;
}

// 二叉树上查找最大值
function getMax() {
    var current = this.root;
    while(!(current.right == null)) {
        current = current.right;
    }
    return current.data;
}

// 查找给定值
function find(data) {
    var current = this.root;
    while(current != null) {
        if(current.data == data) {
            return current;
        }else if(data < current.data) {
            current = current.left;
        }else {
            current = current.right;
        }
    }
    return null;
}

从二叉查找树上删除节点。

原理：从二叉树上删除节点首先要判断当前节点是否包含待删除的数据，如果包含，则删除该节点；如果不包含，则要比较当前节点上的数据和待删除的数据。如果待删除数据小于当前节点上的数据，则要移到当前节点的左子节点继续比较；如果删除的数据大于当前节点上的数据，则移至当前节点的右子节点继续比较。

如果待删除节点是叶子节点(没有子节点的节点)，那么只需要将父节点指向它的链接指向null；

如果待删除的节点只包含一个子节点，那么原本指向它的节点就得做点调整，使其指向它的子节点。

最后，如果待删除节点包含2个子节点，正确的做法有2种，1：要么查找待删除节点左子树上的最大值，要么查找其右子树上的最小值。这里我们选择后一种；

下面是我们删除节点的JS代码如下：

function remove(data) {
    root = removeNode(this.root,data);
}
function getSmallest(node) {
   if (node.left == null) {
      return node;
   }
   else {
      return getSmallest(node.left);
   }
}
function removeNode(node,data) {
    if(node == null) {
        return null;
    }
    if(data == node.data) {
        // 没有子节点的节点
        if(node.left == null && node.right == null) {
            return null;
        } 
        // 没有左子节点的节点
        if(node.left == null) {
            return node.right;
        }
        // 没有右子节点的节点
        if(node.right == null) {
            return node.left;
        }
        // 有2个子节点的节点
        var tempNode = getSmallest(node.right);
        node.data = tempNode.data;
        node.right = removeNode(node.right,tempNode.data);
        return node;
    }else if(data < node.data) {
        node.left = removeNode(node.left,data);
        return node;
    }else {
        node.right = removeNode(node.right,data);
        return node;
    }
}

我们还是以上面的二叉树来分析下代码原理：

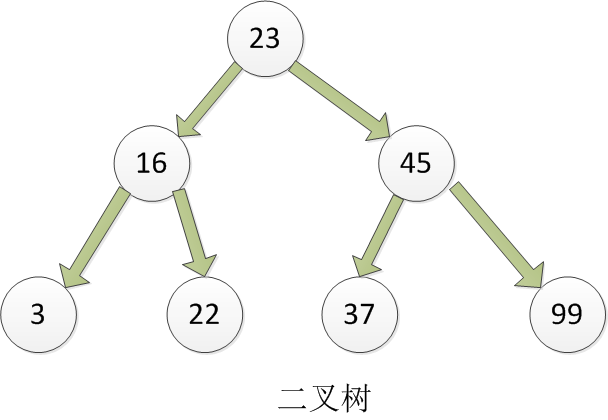
1. 比如我现在要删除根节点为23的节点，代码初始化如下：

   nums.remove(23);

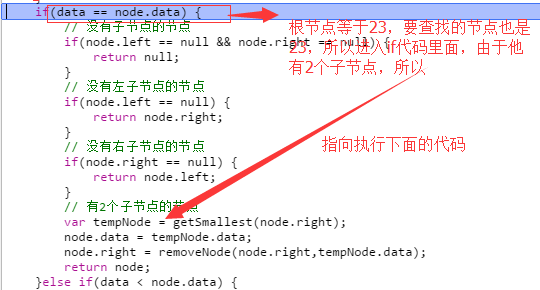
执行这个代码后 var tempNode = getSmallest(node.right); 就指向45的那个节点了，如下：

然后执行下面的获取右子树上的最小值的方法；

function getSmallest(node) {
   if (node.left == null) {
      return node;
   }
   else {
      return getSmallest(node.left);
   }
}

里面使用递归的方式执行代码，当node.left == null 时候，就返回当前node节点；如下：

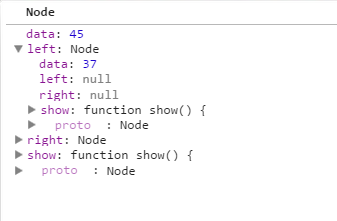
如上所示，当node等于37的时候 就返回node为37的节点。

下面继续执行第二句代码；如下：

node.data = tempNode.data; 那么node.data = 37了；下面是node节点的截图如下：

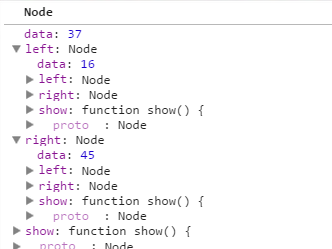
接着继续执行下面的代码

node.right = removeNode(node.right,tempNode.data);

同时又使用递归的方式removeNode()方法；返回如下节点：

所有的JS代码如下：

function Node(data,left,right) {
    this.data = data;
    this.left = left;
    this.right = right;
    this.show = show;
}

function show() {
    return this.data;
}

function BST() {
    this.root = null;
    this.insert = insert;
    this.inOrder = inOrder;
    this.getMin = getMin;
    this.getMax = getMax;
    this.find = find;
    this.remove = remove;
}

function insert(data) {
    var n = new Node(data,null,null);
    if(this.root == null) {
        this.root = n;
    }else {
        var current = this.root;
        var parent;
        while(current) {
            parent = current;
            if(data <  current.data) {
                current = current.left;
                if(current == null) {
                    parent.left = n;
                    break;
                }
            }else {
                current = current.right;
                if(current == null) {
                    parent.right = n;
                    break;
                }
            }
        }
    }
}
// 中序遍历
function inOrder(node) {
    if(!(node == null)) {
        inOrder(node.left);
        console.log(node.show());
        inOrder(node.right);
    }
}

// 先序遍历 
function preOrder(node) {
    if(!(node == null)) {
        console.log(node.show());
        preOrder(node.left);
        preOrder(node.right);
    }
}

// 后序遍历
function postOrder(node) {
    if(!(node == null)) {
        postOrder(node.left);
        postOrder(node.right);
        console.log("后序遍历"+node.show());
    }
}

// 二叉树查找最小值
function getMin(){
    var current = this.root;
    while(!(current.left == null)) {
        current = current.left;
    }
    return current.data;
}

// 二叉树上查找最大值
function getMax() {
    var current = this.root;
    while(!(current.right == null)) {
        current = current.right;
    }
    return current.data;
}

// 查找给定值
function find(data) {
    var current = this.root;
    while(current != null) {
        if(current.data == data) {
            return current;
        }else if(data < current.data) {
            current = current.left;
        }else {
            current = current.right;
        }
    }
    return null;
}

function remove(data) {
    root = removeNode(this.root,data);
}
function getSmallest(node) {
   if (node.left == null) {
      return node;
   }
   else {
      return getSmallest(node.left);
   }
}
function removeNode(node,data) {
    if(node == null) {
        return null;
    }
    if(data == node.data) {
        // 没有子节点的节点
        if(node.left == null && node.right == null) {
            return null;
        } 
        // 没有左子节点的节点
        if(node.left == null) {
            return node.right;
        }
        // 没有右子节点的节点
        if(node.right == null) {
            return node.left;
        }
        // 有2个子节点的节点
        var tempNode = getSmallest(node.right);
        node.data = tempNode.data;
        node.right = removeNode(node.right,tempNode.data);
        return node;
    }else if(data < node.data) {
        node.left = removeNode(node.left,data);
        return node;
    }else {
        node.right = removeNode(node.right,data);
        return node;
    }
}
代码初始化如下：
var nums = new BST();
nums.insert(23);
nums.insert(45);
nums.insert(16);
nums.insert(37);
nums.insert(3);
nums.insert(99);
nums.insert(22);
var min = nums.getMin();
console.log(min);
var max = nums.getMax();
console.log(max);
var value = nums.find("45");
console.log(value);
nums.remove(23);