WP7-XNA 3D开发 模型变换(缩放、移动、旋转)
前文已经简单介绍模型的显示方式。本文来介绍模型的控制(缩放、移动、旋转)
先来个模型这回给模型先加个贴图 为了好看。。 - -
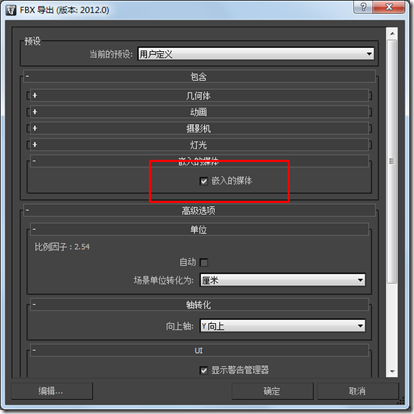
因为这回的模型包括贴图,再导出时记得勾选包含嵌入的媒体
然后新建一个项目,就叫ModelControl吧 ╮(╯▽╰)╭, 先让模型显示出来
1: protected override void Draw(GameTime gameTime)
2: {
3: GraphicsDevice.Clear(Color.CornflowerBlue);
4:
5: // TODO: Add your drawing code here
6: Matrix world = Matrix.Identity;
7: Matrix view = Matrix.CreateLookAt(new Vector3(0, 0, 50),Vector3.Zero,Vector3.Up);
8: Matrix projection = Matrix.CreatePerspectiveFieldOfView(MathHelper.PiOver4, GraphicsDevice.Viewport.AspectRatio, 0.1f, 50f);
9:
10: model.Draw(world, view, projection);
11:
12: base.Draw(gameTime);
13: }
对模型的变换其实就是对模型在世界中的矩阵进行变换,就是上面代码中的world(理解成模型自己的世界吧,这个世界和真实世界时相对关系,对world的变换就是模型的小世界相对于整个真实世界的相对变换),其实代码中设置world=Martix.Identity,就是设施模型世界和真实世界重合,阿米托福~~
这里有必要提到一个神奇的数学知识——矩阵(具体不做赘述,请自行百度)。
矩阵分为两类(未考证),用来表示模型位置的位置矩阵,和用来表示模型变化的变换(平移、缩放、旋转)矩阵。然后就是矩阵最欢乐的一个性质,一个表示位置的矩阵乘一个变换矩阵得到的结果矩阵就是这个模型在那个位置按照变换矩阵变化后的状态。更欢乐地一点是可以用多个变换矩阵相乘得到的结果就是这么多变换以后的结果,也就是可以用一个矩阵乘的结果来代替这一堆变换矩阵后的结果。(这玩意太抽象,好理解 不好描述,看了下面例子就会明白。。。╮(╯▽╰)╭)
矩阵是一个很深得学科 ,也是做3D的基本功,好在XNA提供了N多方法来方便的创建矩阵。具体这里给出两篇文章是用来简单介绍矩阵的。
http://www.cnblogs.com/desmend/archive/2008/09/20/1294880.html
http://blog.sina.com.cn/s/blog_6cccb1630100m24z.html
模型的缩放
Matrix.CreateScale(float scale); 用来创建缩放矩阵,参数表示缩放比例。
比如。。我们可以这么做,让我们的模型变成原来的2倍大小。
1: protected override void Draw(GameTime gameTime)
2: {
3: GraphicsDevice.Clear(Color.CornflowerBlue);
4:
5: // TODO: Add your drawing code here
6: Matrix world = Matrix.Identity;
7: Matrix view = Matrix.CreateLookAt(new Vector3(0, 0, 50),Vector3.Zero,Vector3.Up);
8: Matrix projection = Matrix.CreatePerspectiveFieldOfView(MathHelper.PiOver4, GraphicsDevice.Viewport.AspectRatio, 0.1f, 50f);
9:
10: Matrix change = Matrix.CreateScale(2.0f);//创建一个缩放矩阵,让模型变成原来的两倍大小
11: world *= change;//让模型矩阵乘上变化矩阵的结果
12:
13: model.Draw(world, view, projection);//显示变化后的模型
14:
15: base.Draw(gameTime);
16: }
对比下(使用前 vs 使用后)
模型的移动
Matrix.CreateTranslation(Vector3 translation); 用来创建位移矩阵,参数是表示位移方向和距离的矢量。
比如。。我们可以这么做,让我们的模型向X轴正方向移动10CM(模型半径我创建的时候设置的是5cm);
1: protected override void Draw(GameTime gameTime)
2: {
3: GraphicsDevice.Clear(Color.CornflowerBlue);
4:
5: // TODO: Add your drawing code here
6: Matrix world = Matrix.Identity;
7: Matrix view = Matrix.CreateLookAt(new Vector3(0, 0, 50),Vector3.Zero,Vector3.Up);
8: Matrix projection = Matrix.CreatePerspectiveFieldOfView(MathHelper.PiOver4, GraphicsDevice.Viewport.AspectRatio, 0.1f, 50f);
9:
10: model.Draw(world, view, projection);//显示变化前的模型
11:
12: Matrix change = Matrix.CreateTranslation(new Vector3(10, 0, 0));//让模型向X轴正方向移动10cm
13: world *= change;//让模型矩阵乘上变化矩阵的结果
14:
15: model.Draw(world, view, projection);//显示变化后的模型
16:
17: base.Draw(gameTime);
18: }
效果如下
模型的旋转
旋转的情况比较多.XNA也提供了多个创建不同旋转方式的方法。
我选我觉得比较用的上的进行介绍。
可以参考之前提到的这篇文章 (XNA中三维空间物体的几种旋转方法)
首先是最常用到的Matrix. CreateRotationX、Matrix. CreateRotationY、Matrix. CreateRotationZ三个方法(参数是一个float类型的弧度(角度到弧度的转换可以使用MathHelper.ToRadians(旋转度数)));
这3个方法分别表示模型沿X\Y\Z三个轴旋转。旋转的方向按照右手螺旋定则(右手伸出大拇指做出“你真棒”的手势,然后把拇指沿着旋转轴正方向的时候,四指握拳的方向就是当前轴的正方向)
沿着X轴旋转90°
1: protected override void Draw(GameTime gameTime)
2: {
3: GraphicsDevice.Clear(Color.CornflowerBlue);
4:
5: // TODO: Add your drawing code here
6: Matrix world = Matrix.Identity;
7: Matrix view = Matrix.CreateLookAt(new Vector3(0, 0, 50),Vector3.Zero,Vector3.Up);
8: Matrix projection = Matrix.CreatePerspectiveFieldOfView(MathHelper.PiOver4, GraphicsDevice.Viewport.AspectRatio, 0.1f, 50f);
9:
10: Matrix change = Matrix.CreateRotationX(MathHelper.ToRadians(90));//模型沿着X轴旋转90度
11: world *= change;//让模型矩阵乘上变化矩阵的结果
12:
13: model.Draw(world, view, projection);//显示变化后的模型
14:
15: base.Draw(gameTime);
16: }
结果如下
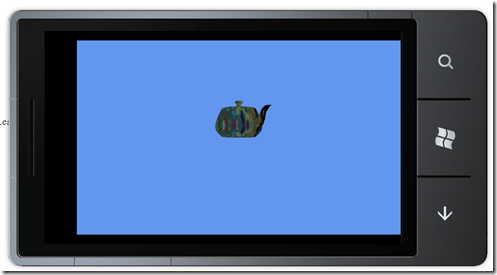
同理,沿着Y轴逆向旋转45°
1: Matrix change = Matrix.CreateRotationY(MathHelper.ToRadians(-45));
结果如下
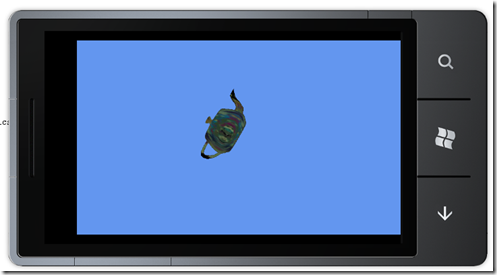
同理,沿着Z轴旋转60°
1: Matrix change = Matrix.CreateRotationZ(MathHelper.ToRadians(60));
结果如下
最后介绍一种,除了沿着轴旋转外,个人认为比较常用的方法Matrix.CreateFromAxisAngle,绕任意矢量旋转,参数有两个,一个是作为轴的矢量,一个是旋转弧度。(旋转方向依然按照右手法则)
比如沿着(1,1,0)这个轴 旋转90°
1: Matrix change = Matrix.CreateFromAxisAngle(new Vector3(1, 1, 0), MathHelper.ToRadians(90));
结果如下(由于投影矩阵设置的不太合适 有点哈哈镜效果。。。见谅。。)
好了 模型的变换介绍完毕。收工~~
出处:http://tugeler.cnblogs.com/
本文版权归作者所,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。









【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· winform 绘制太阳,地球,月球 运作规律
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理