深度学习的反向传播笔记
深度学习反向学习方法可以说是神经网络中比较难懂的一块了,主要是公式的推导和计算要有一些数学知识
可以说这个思想的精髓是数学也不为过
因为都是数学公式表达式,不知道怎么发,直接转成了图片,可以放大查


这里的误差推荐用平方差



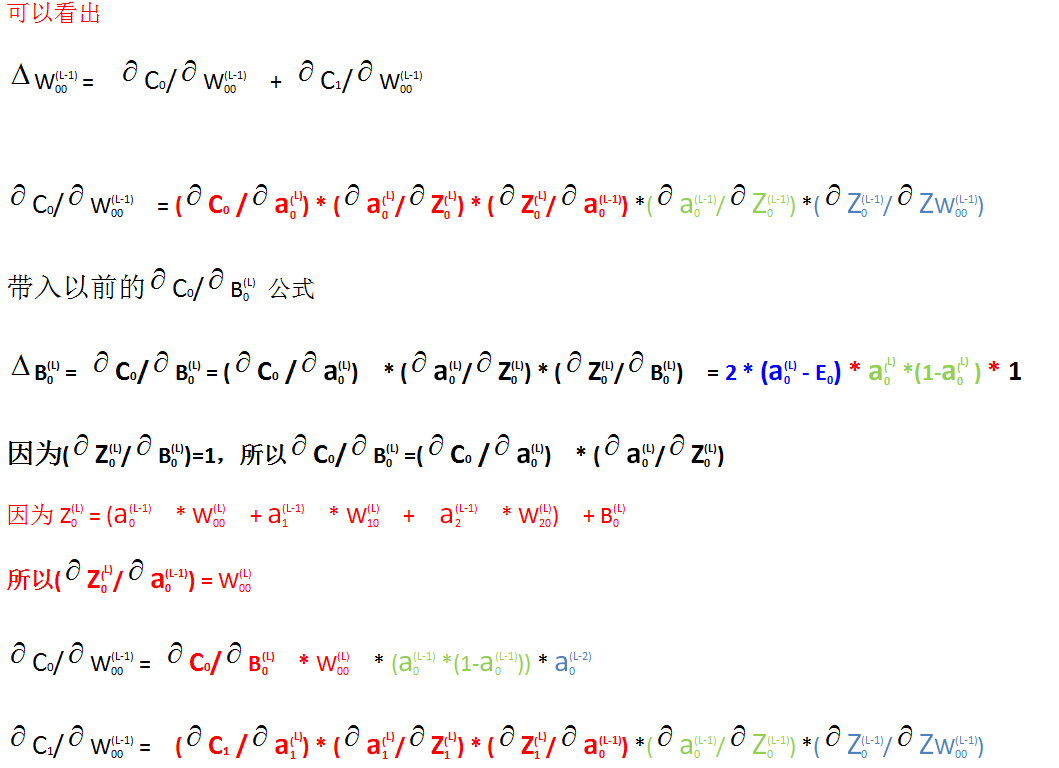



每次学习神经网络,看到反向传播都有点蒙,做个标件,以后如果还有什么再补充~~~
2019年9月24号修正
1 backprop(Dwtab, Dbtab, Tlist, Val, N) -> 2 {_, Tname} = lists:keyfind(N-1, 1, Tlist), 3 V = ets:tab2list(Tname), 4 {_, Ntname} = lists:keyfind(N, 1, Tlist), 5 ok = do_work2(Dwtab, Dbtab, Ntname, N, Val, lists:nth(N, ?NETWORK), V), 6 backprop(Dwtab, Dbtab, Tlist, N-1). 7 8 do_work2(_, _, _, _, _, 0, _) -> 9 ok; 10 do_work2(Dwtab, Dbtab, Tname, N, Val, H, V) -> 11 [{_, A}]= ets:lookup(Tname, H), 12 E = lists:nth(H, Val), 13 Num = lists:nth(N, ?NETWORK), 14 Dx = (2/Num) * (A-E) * A * (1-A), 15 _ = [ets:insert(Dwtab, {[N-1, X], [N, H], Dx*Y})|| {X, Y} <- V ], 16 _ = ets:insert(Dbtab, {N, H, Dx}), 17 do_work2(Dwtab, Dbtab, Tname, N, Val, H-1, V). 18 19 20 backprop(Dwtab, Dbtab, _, 1) -> 21 Dwl = ets:tab2list(Dwtab), 22 Dbl = ets:tab2list(Dbtab), 23 ?SERVERNAME ! {dx, Dwl, Dbl}; 24 backprop(Dwtab, Dbtab, Tlist, N) -> 25 {_, Tname} = lists:keyfind(N-1, 1, Tlist), 26 V = ets:tab2list(Tname), 27 {_, Ntname} = lists:keyfind(N, 1, Tlist), 28 ok = do_work3(Dwtab, Dbtab, Ntname, N, lists:nth(N, ?NETWORK), V), 29 backprop(Dwtab, Dbtab, Tlist, N-1). 30 31 32 do_work3(_, _, _, _, 0, _) -> 33 ok; 34 do_work3(Dwtab, Dbtab, Tname, N, H, V) -> 35 [{_, A}]= ets:lookup(Tname, H), 36 W = [ X || [_, X] <- lists:sort(ets:match(?WTNAME, {[N, H], '$1', '$2'}))], 37 D = [ X || [_, X] <- lists:sort(ets:match(Dbtab, {N+1, '$1', '$2'}))], 38 Dx = dot(W, D) * A * (1-A), 39 _ = [ets:insert(Dwtab, {[N-1, X], [N, H], Dx*Y})|| {X, Y} <- V ], 40 _ = ets:insert(Dbtab, {N, H, Dx}), 41 do_work3(Dwtab, Dbtab, Tname, N, H-1, V).
用erlang实现的反向传播代码,和python比速度慢一点,还有优化空间
2021年11月25号再次修正,python实现比erlang或者golang快很多,python的numpy库太强大了~~~
网上的python代码如下
1 """ 2 network.py 3 ~~~~~~~~~~ 4 5 A module to implement the stochastic gradient descent learning 6 algorithm for a feedforward neural network. Gradients are calculated 7 using backpropagation. Note that I have focused on making the code 8 simple, easily readable, and easily modifiable. It is not optimized, 9 and omits many desirable features. 10 """ 11 12 #### Libraries 13 # Standard library 14 import random 15 16 # Third-party libraries 17 import numpy as np 18 19 class Network(object): 20 21 def __init__(self, sizes): 22 """The list ``sizes`` contains the number of neurons in the 23 respective layers of the network. For example, if the list 24 was [2, 3, 1] then it would be a three-layer network, with the 25 first layer containing 2 neurons, the second layer 3 neurons, 26 and the third layer 1 neuron. The biases and weights for the 27 network are initialized randomly, using a Gaussian 28 distribution with mean 0, and variance 1. Note that the first 29 layer is assumed to be an input layer, and by convention we 30 won't set any biases for those neurons, since biases are only 31 ever used in computing the outputs from later layers.""" 32 self.num_layers = len(sizes) 33 self.sizes = sizes 34 self.biases = [np.random.randn(y, 1) for y in sizes[1:]] 35 self.weights = [np.random.randn(y, x) 36 for x, y in zip(sizes[:-1], sizes[1:])] 37 38 def SGD(self, training_data, epochs, mini_batch_size, eta, 39 test_data=None): 40 """Train the neural network using mini-batch stochastic 41 gradient descent. The ``training_data`` is a list of tuples 42 ``(x, y)`` representing the training inputs and the desired 43 outputs. The other non-optional parameters are 44 self-explanatory. If ``test_data`` is provided then the 45 network will be evaluated against the test data after each 46 epoch, and partial progress printed out. This is useful for 47 tracking progress, but slows things down substantially.""" 48 if test_data: n_test = len(test_data) 49 n = len(training_data) 50 for j in range(epochs): 51 random.shuffle(training_data) 52 mini_batches = [ 53 training_data[k:k+mini_batch_size] 54 for k in range(0, n, mini_batch_size)] 55 for mini_batch in mini_batches: 56 self.update_mini_batch(mini_batch, eta) 57 if test_data: 58 print ("Epoch {0}: {1} / {2}".format( 59 j, self.evaluate(test_data), n_test)) 60 else: 61 print ("Epoch {0} complete".format(j)) 62 63 def update_mini_batch(self, mini_batch, eta): 64 """Update the network's weights and biases by applying 65 gradient descent using backpropagation to a single mini batch. 66 The ``mini_batch`` is a list of tuples ``(x, y)``, and ``eta`` 67 is the learning rate.""" 68 nabla_b = [np.zeros(b.shape) for b in self.biases] 69 nabla_w = [np.zeros(w.shape) for w in self.weights] 70 for x, y in mini_batch: 71 delta_nabla_b, delta_nabla_w = self.backprop(x, y) 72 nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)] 73 nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)] 74 self.weights = [w-(eta/len(mini_batch))*nw 75 for w, nw in zip(self.weights, nabla_w)] 76 self.biases = [b-(eta/len(mini_batch))*nb 77 for b, nb in zip(self.biases, nabla_b)] 78 79 def backprop(self, x, y): 80 """Return a tuple ``(nabla_b, nabla_w)`` representing the 81 gradient for the cost function C_x. ``nabla_b`` and 82 ``nabla_w`` are layer-by-layer lists of numpy arrays, similar 83 to ``self.biases`` and ``self.weights``.""" 84 nabla_b = [np.zeros(b.shape) for b in self.biases] 85 nabla_w = [np.zeros(w.shape) for w in self.weights] 86 # feedforward 87 activation = x 88 activations = [x] # list to store all the activations, layer by layer 89 zs = [] # list to store all the z vectors, layer by layer 90 for b, w in zip(self.biases, self.weights): 91 # print(b) 92 # print(w) 93 # print(activation) 94 z = np.dot(w, activation)+b 95 zs.append(z) 96 activation = sigmoid(z) 97 activations.append(activation) 98 # print("zs:", zs) 99 print("activations:", activations) 100 # backward pass 101 delta = self.cost_derivative(activations[-1], y) * \ 102 sigmoid_prime(zs[-1]) 103 nabla_b[-1] = delta 104 nabla_w[-1] = np.dot(delta, activations[-2].transpose()) 105 # Note that the variable l in the loop below is used a little 106 # differently to the notation in Chapter 2 of the book. Here, 107 # l = 1 means the last layer of neurons, l = 2 is the 108 # second-last layer, and so on. It's a renumbering of the 109 # scheme in the book, used here to take advantage of the fact 110 # that Python can use negative indices in lists. 111 for l in range(2, self.num_layers): 112 z = zs[-l] 113 sp = sigmoid_prime(z) 114 delta = np.dot(self.weights[-l+1].transpose(), delta) * sp 115 nabla_b[-l] = delta 116 nabla_w[-l] = np.dot(delta, activations[-l-1].transpose()) 117 # print("nabla_b:", nabla_b) 118 # print("nabla_w:", nabla_w) 119 return (nabla_b, nabla_w) 120 121 def evaluate(self, test_data): 122 """Return the number of test inputs for which the neural 123 network outputs the correct result. Note that the neural 124 network's output is assumed to be the index of whichever 125 neuron in the final layer has the highest activation.""" 126 test_results = [(np.argmax(self.feedforward(x)), y) 127 for (x, y) in test_data] 128 return sum(int(x == y) for (x, y) in test_results) 129 130 def cost_derivative(self, output_activations, y): 131 """Return the vector of partial derivatives \partial C_x / 132 \partial a for the output activations.""" 133 return (output_activations-y) 134 135 #### Miscellaneous functions 136 def sigmoid(z): 137 """The sigmoid function.""" 138 return 1.0/(1.0+np.exp(-z)) 139 140 def sigmoid_prime(z): 141 """Derivative of the sigmoid function.""" 142 return sigmoid(z)*(1-sigmoid(z))
使用golang改写了一下,速度快了不少,可是golang的float64精度不够,准确率没python好
//向前传播函数,根据权重和偏移算出结果
func feedforward(input []float64) ([]float64, [][]float64) {
var val [][]float64
val=append(val, input)
for i1, v1 := range wei {
var out []float64
for i2, v2 := range v1 {
var v float64
for i3, v3 := range v2 {
v = v + v3 * input[i3]
}
out = append(out, sigmoid(v + bas[i1][i2]))
}
val = append(val, out)
input = out
}
return input, val
}
//反向传播函数,根据偏差修改权重和偏移
func backprop(val [][]float64, exp []float64) ([][][]float64, [][]float64) {
var dwl [][][]float64
var dbl [][]float64
lnum := len(val)
var wll [][]float64
var bll []float64
// fmt.Println("+++++++len(val[lnum-1]):++++++", len(val[lnum-1]))
for i,v := range exp {
a := val[lnum-1][i]
// dx := 2.0/float64(len(val[lnum-1])) * (a-v) * a * (1-a)
dx := (a-v) * a * (1-a)
var wl []float64
for _, v1 := range val[lnum-2] {
wl = append(wl, dx*v1)
}
wll = append(wll, wl)
bll = append(bll, dx)
}
dwl = append(dwl, wll)
dbl = append(dbl, bll)
// fmt.Println("dbl:", dbl)
// fmt.Println("dwl:", dwl)
return backprop_2(val, dbl, dwl)
}
//反向传播2
func backprop_2(val,dbl [][]float64, dwl [][][]float64) ([][][]float64, [][]float64) {
lnum := len(wei)
// fmt.Println("lnum:", lnum)
for i:=1; i<lnum; i++ {
// fmt.Println("i:", i)
var wll [][]float64
var bll []float64
for i1, v1 := range val[lnum-i] {
// fmt.Println("i1:", i1)
var v float64
var wl []float64
for i2, v2 := range dbl[i-1] {
// fmt.Println("i2:", i2)
v = v + (wei[lnum-i][i2][i1]) * v2
}
dx := v * v1 * (1-v1)
for _, v3 := range val[lnum-i-1] {
// fmt.Println("i3:", i3)
wl = append(wl, dx*v3)
}
wll = append(wll, wl)
bll = append(bll, dx)
}
dwl = append(dwl, wll)
dbl = append(dbl, bll)
// fmt.Println("dbl:", dbl)
// fmt.Println("dwl:", dwl)
}
// fmt.Println("dwl:", dwl)
// fmt.Println("dbl:", dbl)
return dwl, dbl
}
//工作进程并发
func work(cnt int, input, exp [][]float64) {
var wch = make(chan [][][]float64, cnt)
var bch = make(chan [][]float64, cnt)
defer close(wch)
defer close(bch)
for i:=0; i<cnt; i++ {
go func(wc chan <- [][][]float64, bc chan <- [][]float64, in, ex []float64) {
_, val := feedforward(in)
// fmt.Println("now out:", out)
// fmt.Println("now val:", val)
dw, db := backprop(val, ex)
wc <- dw
bc <- db
}(wch, bch, input[i], exp[i])
}
var dwall [][][]float64
var dball [][]float64
for i:=0; i<cnt; i++ {
w := <- wch
dwall = addwlist(dwall, w)
b := <- bch
dball = addblist(dball, b)
}
wei = subwlist(wei, dwall, eta/float64(cnt))
bas = subblist(bas, dball, eta/float64(cnt))
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号