LeetCode刷题回顾

目录

• 排序
  • 快速排序
  • 归并排序
  • 插入排序
  • 桶排序（待完成）
• 二分
  • 整数二分查找的模板
  • 数的平方根
  • 按权重随机选择
• 数学问题
  • 快速幂
• 动态规划
  • 斐波那契数列
  • 跳台阶
  • 最大子序和
  • 零钱兑换
• DFS/BFS
  • 深度优先搜索
    • 排列数字
    • 字典序排数
    • n-皇后问题
  • 广度优先搜索
    • 走迷宫
• 最短路问题
  • Floyd算法
• 贪心（待完成）
• 其他（待完成）
  • C++中的cin和cout

排序

快速排序

void quick_sort(vector<int> &vec, int l, int r)
{
    // 递归终止条件 当只有一个元素时已不需要排序 直接返回
    if (l >= r) return;
    // 取数组中[l]作为随机点x的值
    int i = l - 1, j = r + 1, x = vec[l];
    // 调整区间的操作 令左侧的数都 < x 且右侧的数都 > x
    while (i < j)
    {
        while (vec[++i] < x);
        while (vec[--j] > x);
        // 调整后i和j所在的位置就是不满足while条件的位置
        // 如果i在j的左边 证明i是小于j的(由上述while循环的条件得到) 则需要交换
        if (i < j)
            ::swap(vec[i], vec[j]);
    }
    // 递归处理两边 以j为分界线(此时的i要么与j相等,要么比j大1)
    quick_sort(vec, l, j);
    quick_sort(vec, j + 1, r);
}

int main()
{
    vector<int> v{-2, 1, -3, 4, -1, 2, 1, -5, 4};
    quick_sort(v, 0, v.size() - 1);
    for (int i : v)
        cout << i << endl;
    return 0;
}

归并排序

void merge_sort(vector<int>& vec, int l, int r, vector<int>& cachedVec)
{
    // 递归终止条件 当只有一个元素时已不需要排序 直接返回
    if (l >= r) return;
    // 右移一位 代表除以2 (左移3位则代表乘以2^3) 由于运算优先级 优点是可以少打一个括号
    int mid = l + r >> 1;
    // 递归左边和右边
    merge_sort(vec, l, mid, cachedVec);
    merge_sort(vec, mid + 1, r, cachedVec);
    // 归并操作 i代表左半边数组的起点 j代表右半边数组的起点 cachedIndex代表缓存数组的起点
    int i = l, j = mid + 1, cachedIndex = 0;
    // 从两半边数组中选一个小的数放入缓存数组 然后"指针"推进
    while (i <= mid && j <= r)
    {
        if (vec[i] <= vec[j])
            cachedVec[cachedIndex++] = vec[i++];
        else
            cachedVec[cachedIndex++] = vec[j++];
    }
    // TIPS:不可能出现左右都有剩下的情况
    // 如果左边的指针还没移动到底 则将剩下的数搬过去
    while (i <= mid)
        cachedVec[cachedIndex++] = vec[i++];
    // 如果右边的指针还没移动到底 则将剩下的数据搬过去
    while (j <= r)
        cachedVec[cachedIndex++] = vec[j++];

    // 根据本次归并的范围 将缓存数组中的数据搬到原数组对应的位置(缓存数组从头开始搬)
    for (i = l, j = 0; i <= r; i++, j++)
        vec[i] = cachedVec[j];
}

int main()
{
    vector<int> v{-2, 1, -3, 4, -1, 2, 1, -5, 4};
    vector<int> cachedVec(v.size());
    merge_sort(v, 0, v.size() - 1, cachedVec);
    for (int i : v)
        cout << i << endl;
    return 0;
}

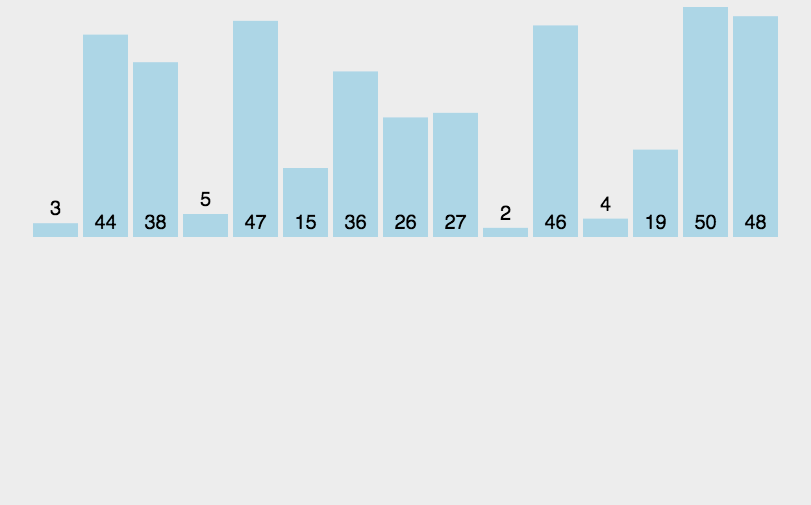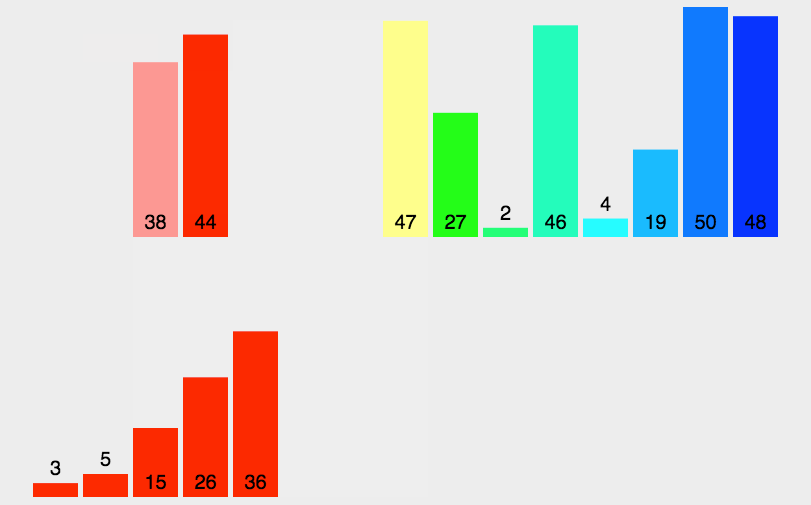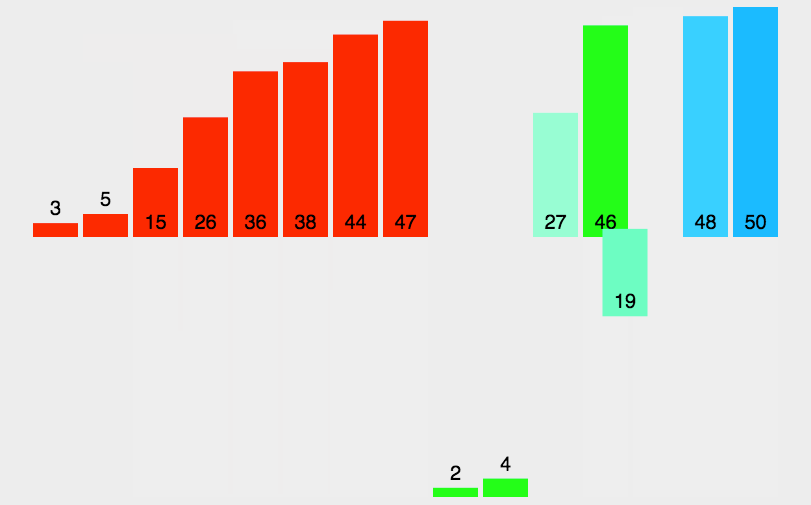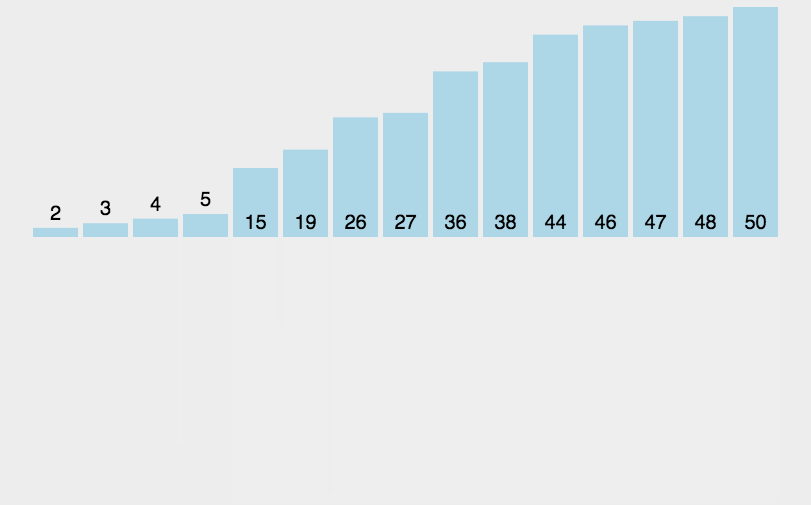
个人对归并过程的小图解

实际过程的由l和r框起来的一小段其实是小于等于cachedVec的，cachedVec与整段v等长。而每次缓存都会从cachedVec的头开始，而不是从与l对齐的位置开始

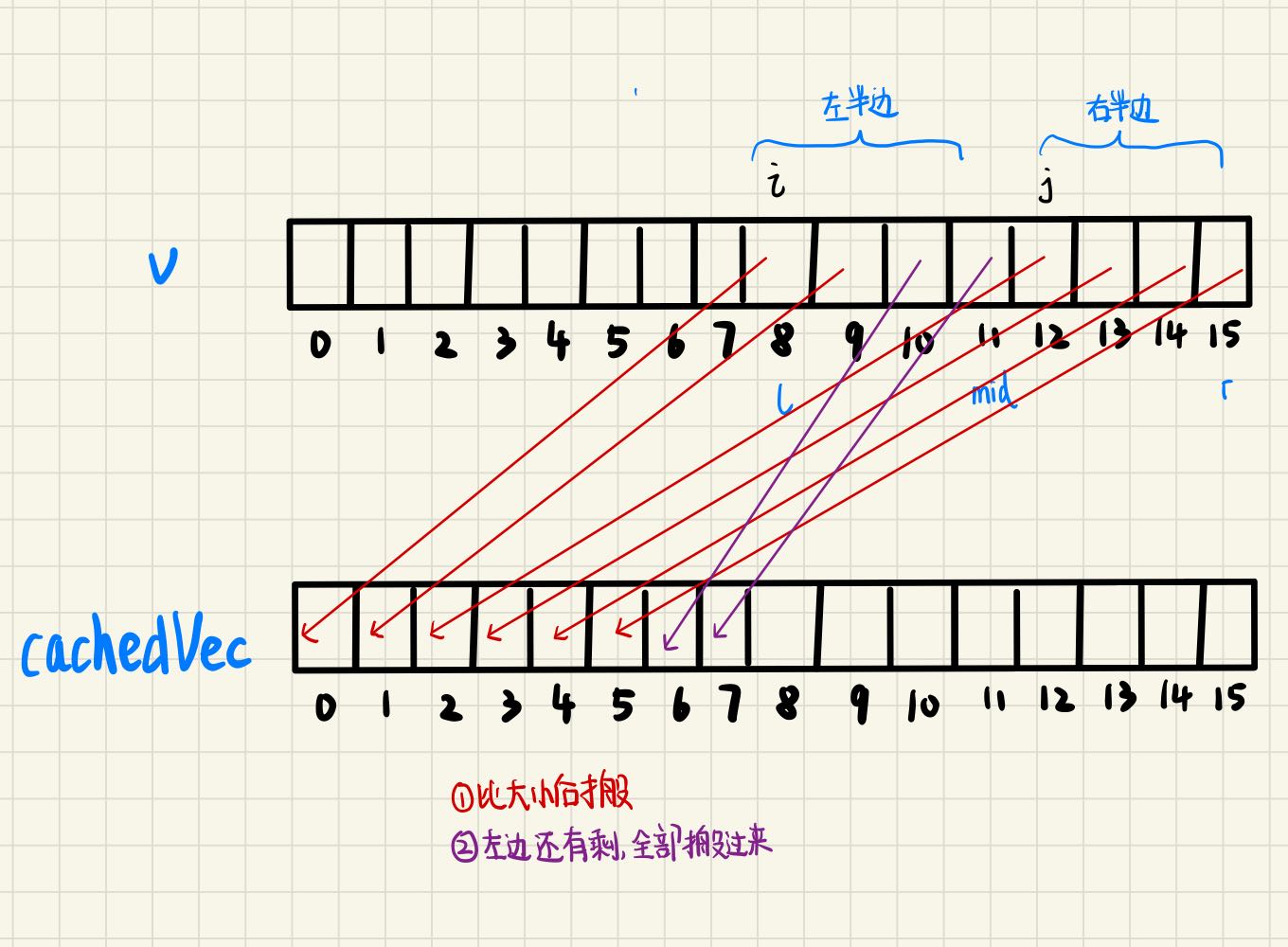
动图解析 该动图的缓存数组表示的不直观 缓存数组并不是一直都与l对齐的

插入排序

template<typename T>
void insert_sort(std::vector<T>& data)
{
    for (std::size_t i = 0; i < data.size(); i++)
    {
        for (std::size_t j = i; j > 0 && data[j] < data[j - 1]; j--)
            std::swap(data[j], data[j - 1]);
    }
}

插入排序的优化，使用二分查找找到当前数据应该插入的位置。平均时间复杂度是O(nlog2 n)

template<typename T>
std::size_t bSearch(const std::vector<T>& data, std::size_t l, std::size_t r, T findData)
{
    while (l < r)
    {
        std::size_t mid = (l + r) / 2;
        if (findData <= data[mid])
            r = mid;
        else
            l = mid + 1;
    }
    return l;
}

template<typename T>
void insert_sort(std::vector<T>& data)
{
    for (std::size_t i = 0; i < data.size(); i++)
    {
        T insertData = data[i];
        // 找到该数据应该插入到哪个地方
        std::size_t insertIndex = bSearch(data, 0, i - 1, insertData);
        // 将该区间往后移
        for (std::size_t from = i; from > insertIndex; from--)
            data[from] = data[from - 1];
        data[insertIndex] = insertData;
    }
}

桶排序（待完成）

二分

整数二分查找的模板

l与r代表数组的左右两端，是可以取到的值，而不是像STL中的end()

int bSearch(int l, int r)
{
    while (l < r)
    {
        int mid = l + r / 2;
        if (check(x)) r = mid;
        else l = mid + 1;
    }
    return l;
}

int bSearch(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 / 2;
        if (check(x)) l = mid;
        else r = mid - 1;
    }
    return l;
}

注解：

• 在答案取不到值的时候，函数返回的值是第一个/最后一个满足check(x)条件的值
• 在while循环结束后，l的值与r相等，所以返回哪个都可以
• check(x)包含取等的情况

以上的注解可能看起来有点抽象，来看这个简单的二分查找例子

vector<int> vec = {1, 2, 3, 3, 3, 5, 6, 9};

int midSearchFirst(int l, int r, int x)
{
    while (l < r)
    {
        int mid = (l + r) / 2;
        // 走左边
        if (x <= vec[mid]) r = mid;
        // 走右边
        else l = mid + 1;
    }
    return l;
}

int midSearchLast(int l, int r, int x)
{
    while (l < r)
    {
        int mid = (l + r + 1) / 2;
        // 走右边
        if (x >= vec[mid]) l = mid;
        // 走左边
        else r = mid - 1;
    }
    return l;
}

• 查找数字3，midSearchFirst找到的是2号位的3，midSearchLast找到的是4号位的3
• 查找数组4，midSearchFirst返回4号位的3，midSearchLast返回五号位的5

在STL中，有lower_bound和upper_bound两种，两者默认操作升序数组（默认为less<T>()）

vector<int> vec = {1, 2, 3, 3, 3, 5, 6, 9};

int main()
{
    // 找大于等于
    cout << *lower_bound(vec.begin(), vec.end(), 5) << endl;	// 5
    // 找大于
    cout << *upper_bound(vec.begin(), vec.end(), 5) << endl;	// 6
}

• 如果找的是数3，那么lower_bound会返回指向第一个3的指针，upper_bound会返回指向最后一个3的指针
• 如果找的是数4，那么lower_bound，upper_bound都会返回指向数字5的指针
• 如果找的是数-100，那么两者都会返回指向数组第一个元素的指针；如果找的是数100，那么两者都会返回vec.end()。因此在查找的时候应该把数据限制在该数组的最大最小范围内

vector<int> vec = {1, 2, 3, 3, 3, 5, 6, 9};
// 找小于等于
std::cout << *std::lower_bound(vec.rbegin(), vec.rend(), 5, greater<>{}) << std::endl;
// 找小于
std::cout << *std::upper_bound(vec.rbegin(), vec.rend(), 5, greater<>{}) << std::endl;

数的平方根

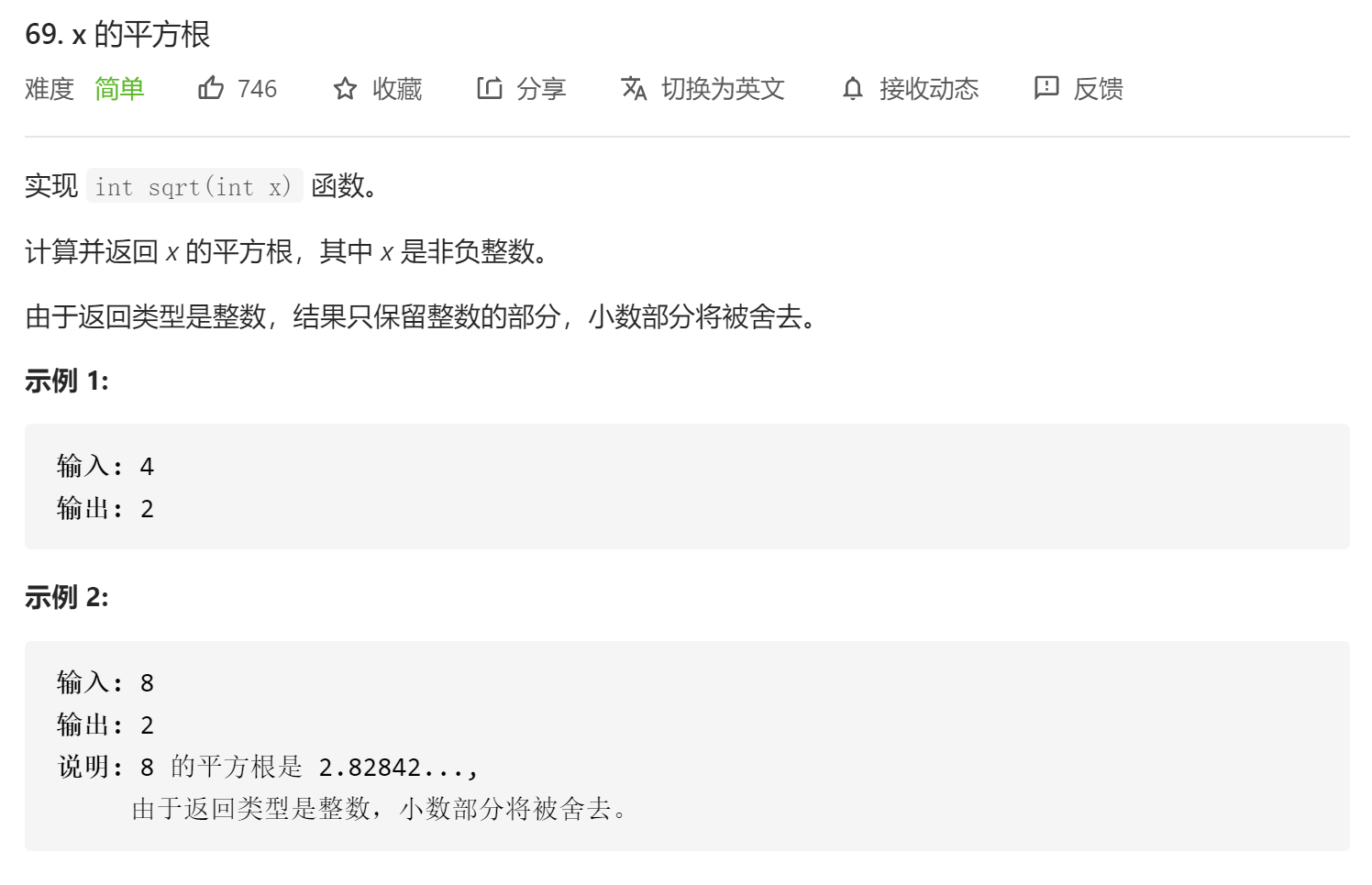
class Solution
{
public:
    long long mySqrt(long long x)
    {
        // 定义边界 从 0-x 开始分
        long long l = 0, r = x;
        while (l < r)
        {
            long long mid = (l + r + 1) / 2;
            // 当x等于5时，要求result为2 也就是说2是满足5 > 2 * 2最后的一个值，因为5 < 3 * 3
            // 所以选用 x >= mid * mid 作为判定条件而不是 x <= mid * mid
            if (x / mid >= mid)
                l = mid;
            else
                r = mid - 1;
        }
        // 返回l或者返回r都行
        return l;
    }
};

按权重随机选择

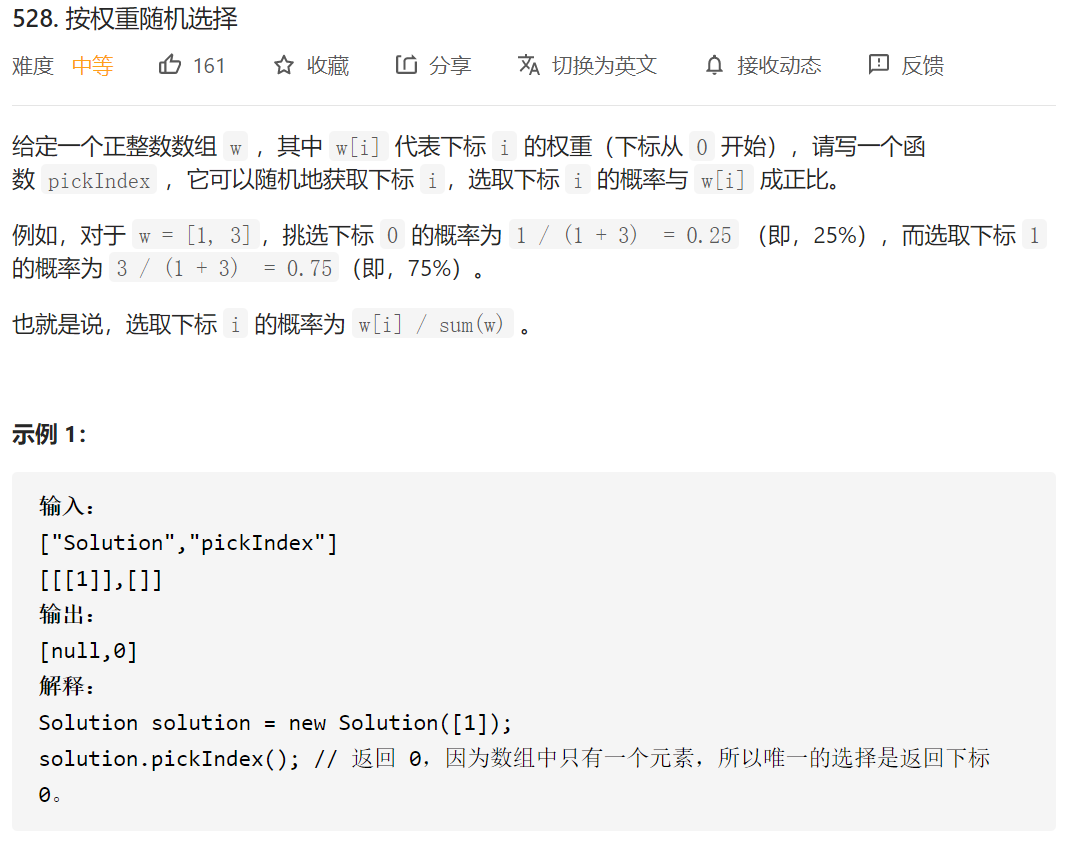
利用前缀和+随机数充当概率模拟，利用二分加快index查找

#include<random>
class Solution {
public:
    default_random_engine e;
    uniform_int_distribution<int> u;

    vector<int> sumVec;

    Solution(vector<int>& w) : sumVec(w.size() + 1), e()
    {
        sumVec[0] = 0;
        for (int i = 1; i < sumVec.size(); i++)
            sumVec[i] = sumVec[i - 1] + w[i - 1];
        u = uniform_int_distribution<int>(0, sumVec[w.size()] - 1);
    }

    int midSearch(int l, int r, int x)
    {
        while (l < r)
        {
            int mid = (l + r + 1) / 2;
            if (x >= sumVec[mid])
                l = mid;
            else
                r = mid - 1;
        }
        return l;
    }

    int pickIndex() {
        return midSearch(0, sumVec.size() - 1, u(e));
    }
};

使用STL自带的二分查找

#include<random>
class Solution {
public:
    default_random_engine e;
    uniform_int_distribution<int> u;
    
    vector<int> sumVec;
    Solution(vector<int>& w) : sumVec(w.size() + 1), e()
    {
        sumVec[0] = 0;
        for (int i = 1; i < sumVec.size(); i++)
            sumVec[i] = sumVec[i - 1] + w[i - 1];
        u = uniform_int_distribution<int>(0, sumVec[w.size()] - 1);
    }
    
    int pickIndex() {
        int randomNum = u(e);
        auto iterator = lower_bound(sumVec.begin(), sumVec.end(), randomNum);
        if (*iterator != randomNum)
            iterator--;
        int index = iterator - sumVec.begin();
        return index;
    }
};

数学问题

快速幂

long long quick_power(int a, int k, int p)
{
    int result = 1;
    while (k)
    {
        if (k & 1)
            result = result * a % p;
        k >>= 1;
        a = a * a % p;
    }
    return result;
}

动态规划

递归的时间复杂度计算 = 递归调用的次数 * 递归函数本身的复杂度

本人对动态规划的理解

• 先写原始递归解法，此时递归开销大，进行了许多重复操作
• 优化为带备忘录的递归解法（对原递归树进行剪枝操作），此时算法思路仍为自顶向下
• 由于备忘录中记录的数据与dp数组中记录的一致，故此时将算法思路转为自底向上，就是动态规划解法

斐波那契数列

原始递归解法，复杂度为 2^n * 1

class Solution 
{
public:
    int fib(int n) 
    {
        if (n == 0) return 0;
        if (n == 1) return 1;
        return (fib(n - 1) + fib(n - 2)) % 1000000007;
    }
};

这种解法具有很多的冗余操作，比如重复计算（递归）的41和40等等，此时利用备忘录能够避免不必要的递归

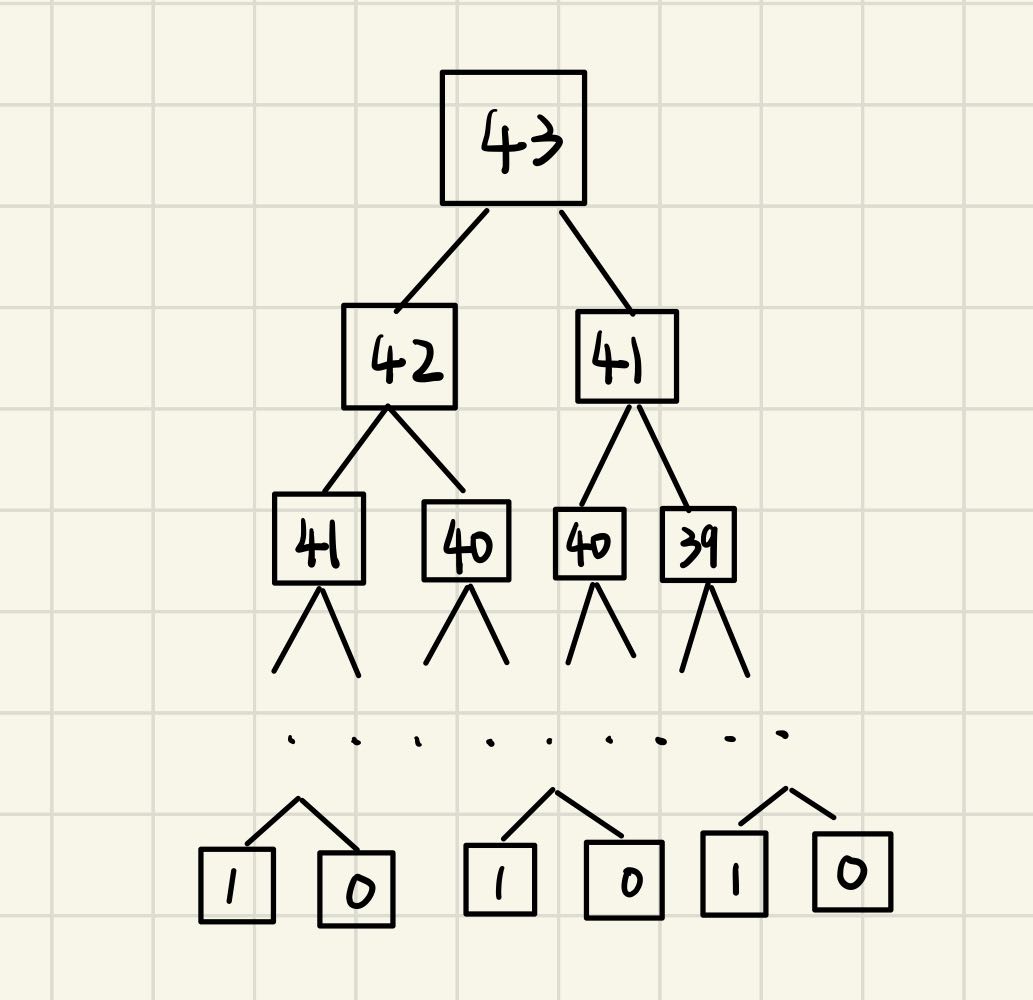
带备忘录的递归解法，相当于对原递归树做了剪枝操作，时间复杂度为o(n)

class Solution 
{
public:
    vector<int> cachedVec;
    int fib(int n) 
    {
        cachedVec = vector<int>(n + 1, -1);
        cachedVec[0] = 0;
        cachedVec[1] = 1;
        return dp(n);
    }

    int dp(int n)
    {
        if (cachedVec[n] != -1) return cachedVec[n];
        cachedVec[n] = (dp(n - 1) + dp(n - 2)) % 1000000007;
        return cachedVec[n];
    }
};

此时的解法已经和动态规划很接近了，区别就在于思路是自顶向下还是自底向上

原先我计算43的时候，需要递归去找42和41，计算42的话，需要去找41和40，这就是自顶向下

而自底向上的思路是，当我知道0和1的时候，就能推出2，而知道了1和2，就能推出3，这是一种自底向上的迭代解法

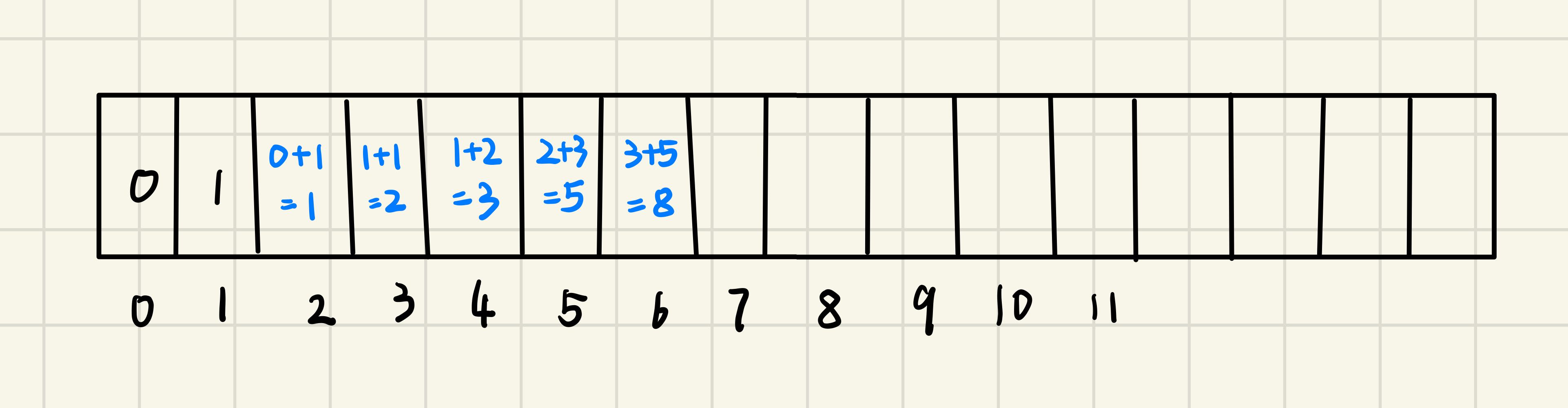
class Solution 
{
public:
    int fib(int n)
    {
        vector<int> dp(n + 1, -1);
        dp[0] = 0;
        dp[1] = 1;
        for (int i = 2; i <= n; i++)
        {
            dp[i] = (dp[i - 1] + dp[i - 2]) % 1000000007;
        }
        return dp[n];
    }
};

而又由于此题每当更新dp数组的值的时候，只需要用到前两个槽的值，所以可以进一步优化，省略掉整个数组，用三个int值代替

class Solution 
{
public:
    int fib(int n) 
    {
        if (n == 0 || n == 1) return n;
        int a = 0, b = 1, result = 0;
        for (int i = 2; i <= n; i++)
        {
            // F(n) = F(n - 2) + F(n - 1);
            result = (a + b) % 1000000007;
            // 往前移
            a = b;
            b = result;
        }
        return result;
    }
};

跳台阶

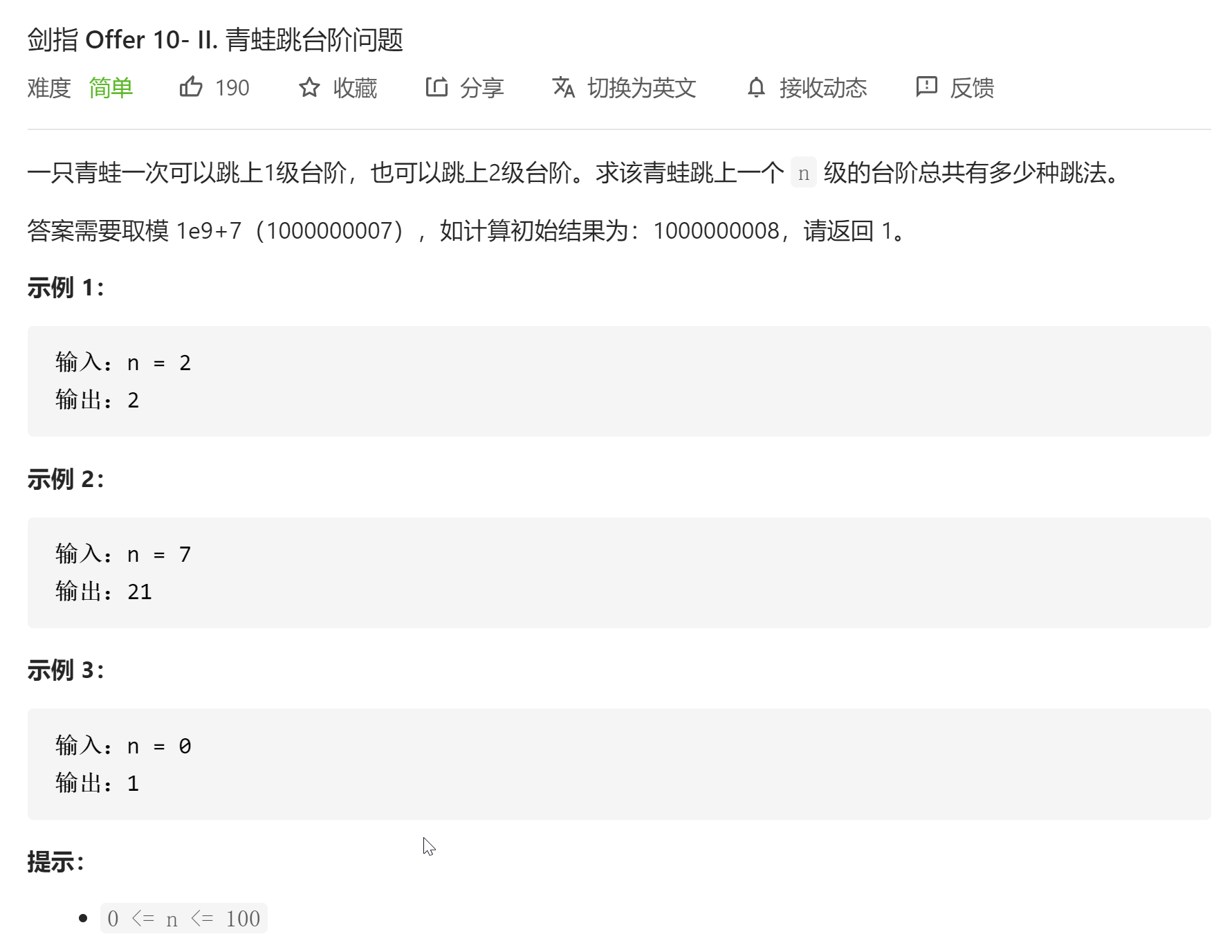
题目分析：小青蛙有两种跳法，要么一次跳一格，要么一次跳两格。假设它需要跳上两格高的楼梯，那么它有两种选择，一次性跳两格高（F(n - 2)），达到终点，F(0) = 1；要么跳一格（F(n - 1)），距离终点还剩下1格，F(1) = 1。

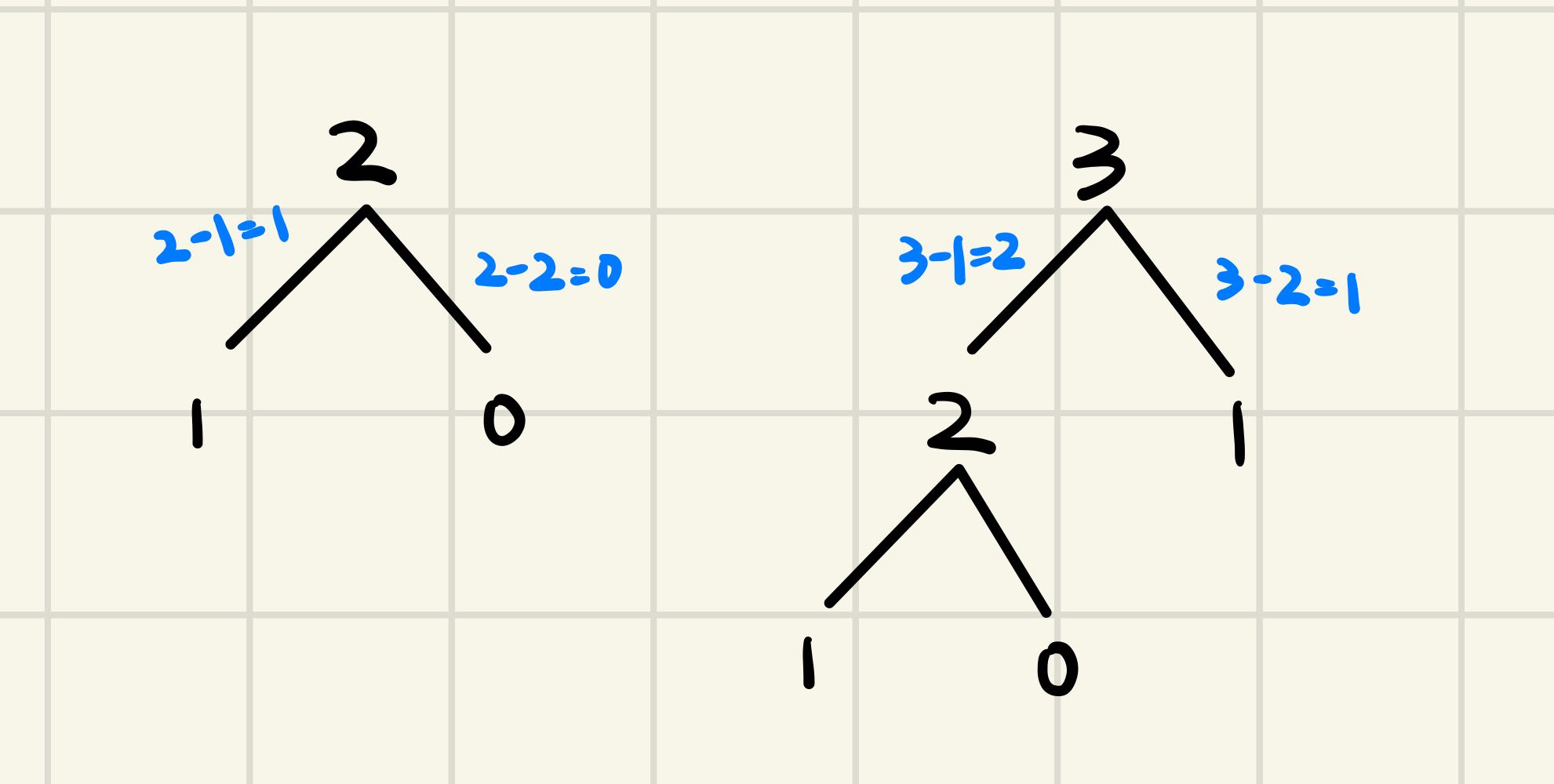
同理，小青蛙想跳三格高的楼梯，一开始也有两种选择，跳2或者跳1，也就是说它跳3格的跳法数量是跳2格的跳法数量 + 跳1格的跳法数量，即F(3) = F(3 - 2) + F(3 - 1)

所以通项为F(n) = F(n - 2) + F(n - 1)，特殊值为F(0) = 1，F(1) = 1

class Solution 
{
public:
    int numWays(int n) {
        if (n == 0) return 1;
        if (n == 1) return 1;
        int a = 1, b = 1, result = 0;
        for (int i = 2; i <= n; i++)
        {
            result = (a + b) % 1000000007;
            a = b;
            b = result;
        }   
        return result;
    }
};

最大子序和

由题意，先建立一个与nums等长的dp数组, 用来记录nums数组中的最大子序和，然后给dp[0]赋特殊值为nums[0]，作为第一个连续子数组的和，同时设置result，用于记录dp数组中的最大值

然后逐个遍历dp数组，比较dp数组中储存的值与nums中下一位的值的和，如果新连续数组的和较小，则终止连续，立nums下一位元素为新连续数组的首位；若和计算结果较大，则连续继续

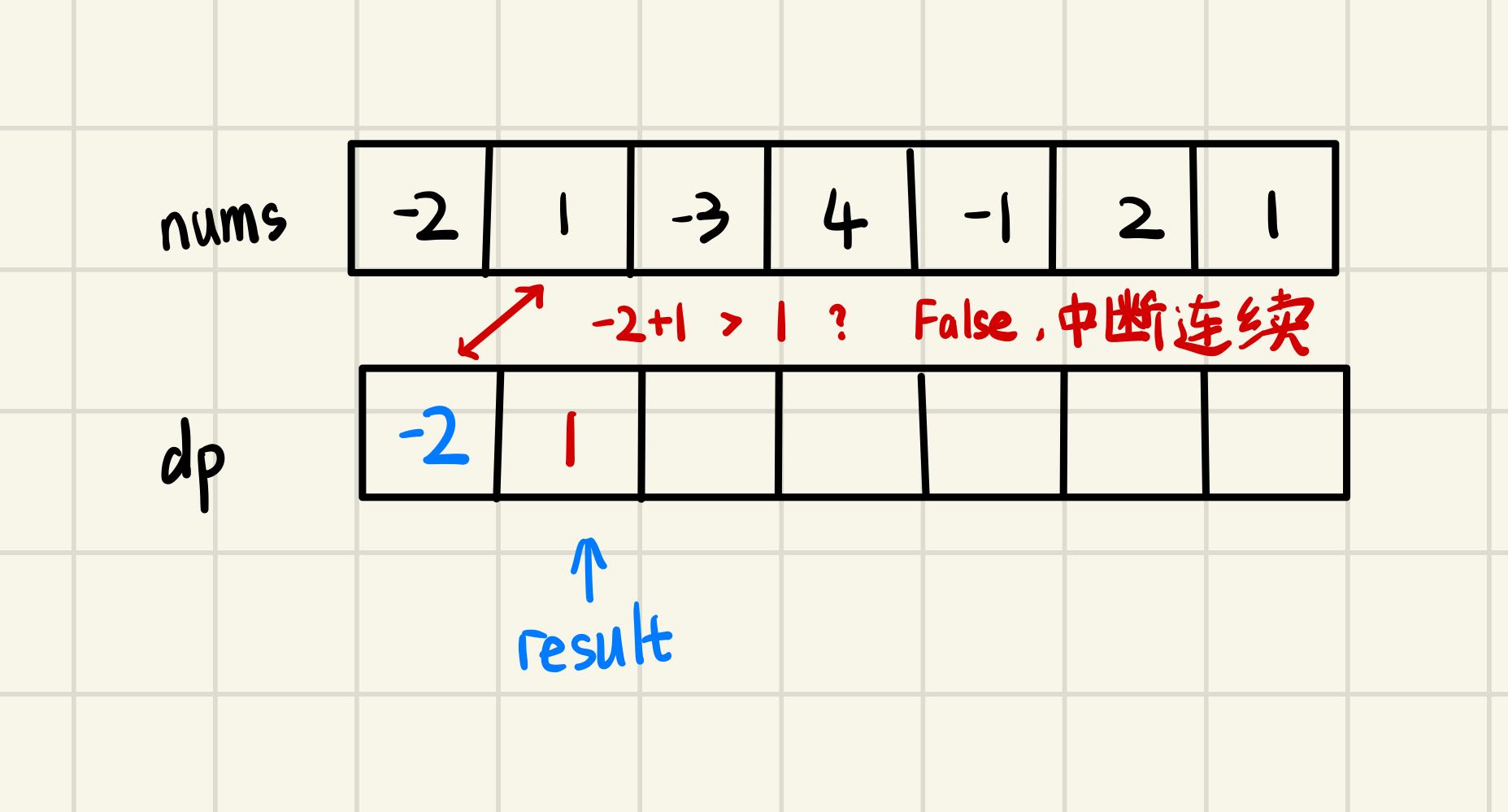
遍历结束时的result就是题目的解

class Solution 
{
public:
    int maxSubArray(const vector<int>& nums)
    {
        auto vecSize = nums.size();
        if (vecSize == 0) return 0;
        int dp = nums[0];
        int result = dp;
        for (int i = 1; i < nums.size(); i++)
        {
            dp = ::max(dp + nums[i], nums[i]);
            result = ::max(result, dp);
        }
        return result;
    }
};

零钱兑换

纯递归解法

class Solution 
{
public:
    int coinChange(const vector<int>& coins, int amount)
    {
        // 零钱太少 不够用
        if (amount < 0) return -1;
        // 刚刚好换完
        if (amount == 0) return 0;
        int result = INT32_MAX;
        for (int coin : coins)
        {
            int subResult = coinChange(coins, amount - coin);
            if (subResult < 0) continue;
            result = ::min(result, subResult + 1);
        }
        // 如果都被continue了 则result仍然是INT32_MAX 也就是说结果是无法兑换
        return result == INT32_MAX ? -1 : result;
    }
};

使用带备忘录的递归解法

class Solution 
{
public:
    vector<int> cachedVec;
    const int defaultValue = -2;
    
    int coinChange(const vector<int>& coins, int amount)
    {
        cachedVec = vector<int>(amount + 1, defaultValue);
        cachedVec[0] = 0;
        return dp(coins, amount);
    }

    int dp(const vector<int>& coins, int amount)
    {
        if (amount < 0) return -1;
        if (cachedVec[amount] != defaultValue)
            return cachedVec[amount];
        int subAmount = INT32_MAX;
        for (int coin : coins)
        {
            // 检测缓存数组中是否已经存有数据
            int subResult = dp(coins, amount - coin);
            if (subResult == -1) continue;
            subAmount = ::min(subAmount, subResult + 1);
        }
        cachedVec[amount] = subAmount == INT32_MAX ? -1 : subAmount;
        return cachedVec[amount];
    }
};

动态规划解法

class Solution 
{
public:
    int coinChange(const vector<int>& coins, int amount)
    {
        vector<int> dp(amount + 1, amount + 1);
        dp[0] = 0;
        for (int i = 1; i < dp.size(); i++)
        {
            for (int coin : coins)
            {
                if (i - coin < 0) continue;
                dp[i] = ::min(dp[i], dp[i - coin] + 1);
            }
        }
        return dp[amount] == amount + 1 ? -1 : dp[amount];
    }
};

DFS/BFS

	数据结构	空间	特点
DFS	stack	O(H)和高度成正比	不具备最短路
BFS	queue	O(2^n)随深度增加指数增长	最短路

深度优先搜索

看起来有点像前序遍历

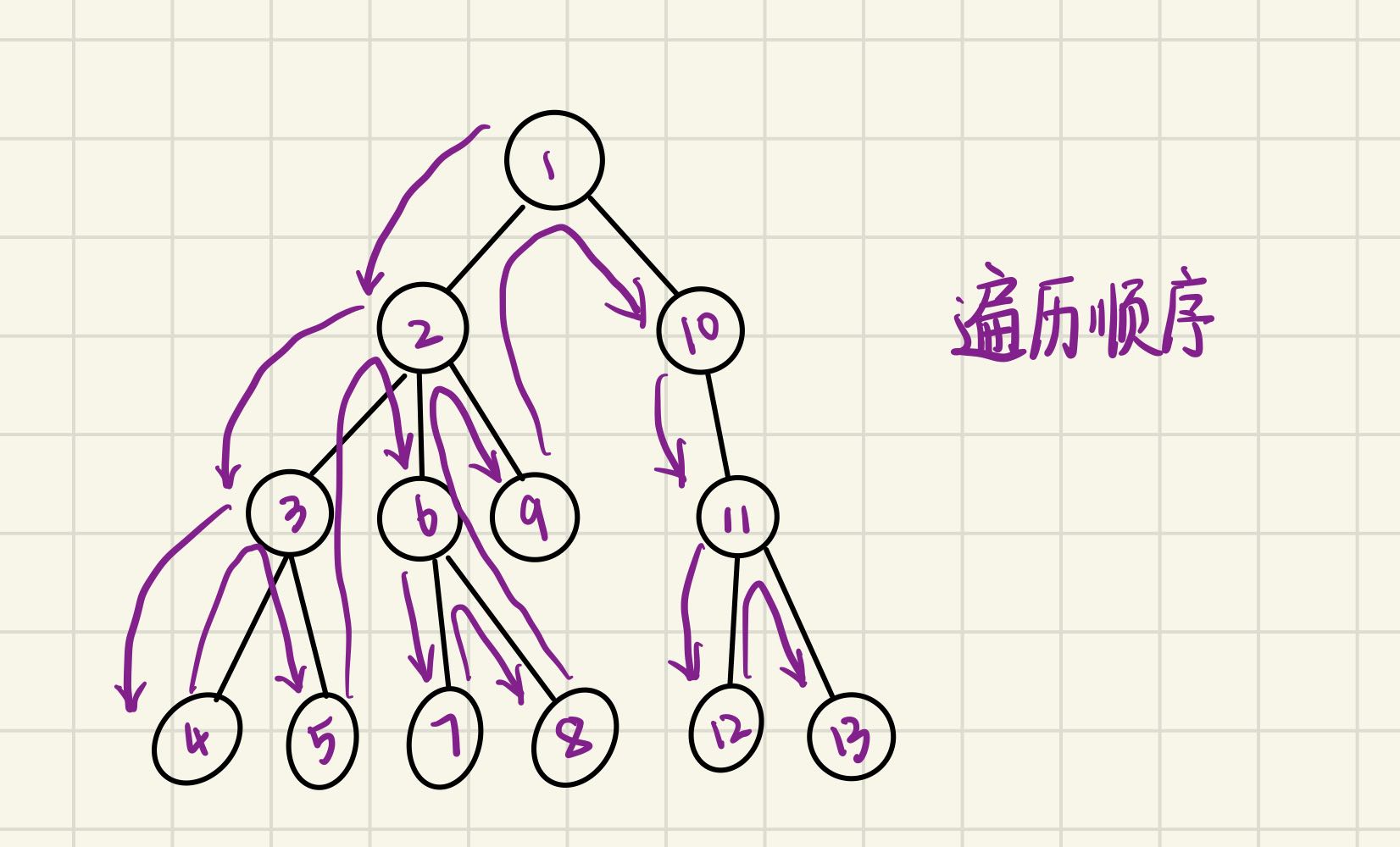
排列数字

使用unordered_map的原因是为了让代码更容易看懂，本题只用vector也可以

class Solution
{
public:
    unordered_map<int, bool> markMap;
    vector<int> sortVec;
    vector<vector<int>> result;

    vector<vector<int>> sortNum(int n)
    {
        sortVec.resize(n);
        dfs(0, n);
        return result;
    }

    void dfs(int index, int n)
    {
        // 递归结束条件
        if (index == n)
        {
            result.push_back(sortVec);
            return;
        }
        for (int i = 1; i <= n; i++)
        {
            // 若i不存在则默认为false
            if (markMap[i] == true)
                continue;
            // 记录并修改标志位
            sortVec[index] = i;
            markMap[i] = true;
            // 往下一层递归
            dfs(index + 1, n);
            // 回溯操作 复原现场
            markMap[i] = false;
        }
    }
};

还可以使用STL进行求解，由于要求的是所有的排列方案，所需需要将数组的初始值定为123

class Solution
{
public:
    vector<vector<int>> sortNum(int n)
    {
       vector<vector<int>> result;
       vector<int> sequence;
       for (int i = 1; i <= n; i++)
           sequence.push_back(i);
        do
            result.push_back(sequence);
        while (next_permutation(sequence.begin(), sequence.end()));
        return result;
    }
};

字典序排数

思路是先假设有9棵十叉树，开始时分别对九棵树进行DFS。每棵树有10个节点（0-9），且深度每进一层，节点的值翻十倍

class Solution {
public:
    vector<int> result;
    vector<int> lexicalOrder(int n) {
        for (int i = 1; i <= 9; i++)
            dfs(i, n);
        return result;
    }

    void dfs(int current, int max)
    {
        if (current > max) return;
        result.push_back(current);
        for (int i = 0; i <= 9; i++)
            dfs(current * 10 + i, max);
    }
};

n-皇后问题

方法一，逐个检查法

class CheckSolution
{
public:
    vector<vector<string>> result;
    vector<string> board;

    vector<vector<string>> solveNQueens(int n)
    {
        board = vector<string>(n, string(n, '.'));
        dfs(0);
        return result;
    }

    void dfs(int lineIndex)
    {
        // 递归结束条件 将棋盘放入结果数组中
        if (lineIndex == board.size())
            result.push_back(board);
        else
        {
            // 当前行逐个遍历
            for (int i = 0; i < board.size(); i++)
            {
                // 检查是否符合皇后放置条件
                if (!canPlace(lineIndex, i))
                    continue;
                // 符合条件 放置皇后
                board[lineIndex][i] = 'Q';
                // 递归进入下一行
                dfs(lineIndex + 1);
                // 恢复现场
                board[lineIndex][i] = '.';
            }
        }
    }

    bool canPlace(int lineIndex, int columnIndex)
    {
        //检查正上方
        for (int i = 0; i < lineIndex; i++)
            if (board[i][columnIndex] == 'Q')
                return false;
        //检查右斜上方
        for (int i = lineIndex - 1, j = columnIndex + 1; i >= 0 && j < board.size(); i--, j++)
            if (board[i][j] == 'Q')
                return false;
        //检查左斜上方
        for (int i = lineIndex - 1, j = columnIndex - 1; i >= 0 && j >= 0; i--, j--)
            if (board[i][j] == 'Q')
                return false;
        // 只需要检查上方部分的棋盘 并且同行不需要检测 因为一行只有一个棋子
        return true;
    }
};

方法二，标记法

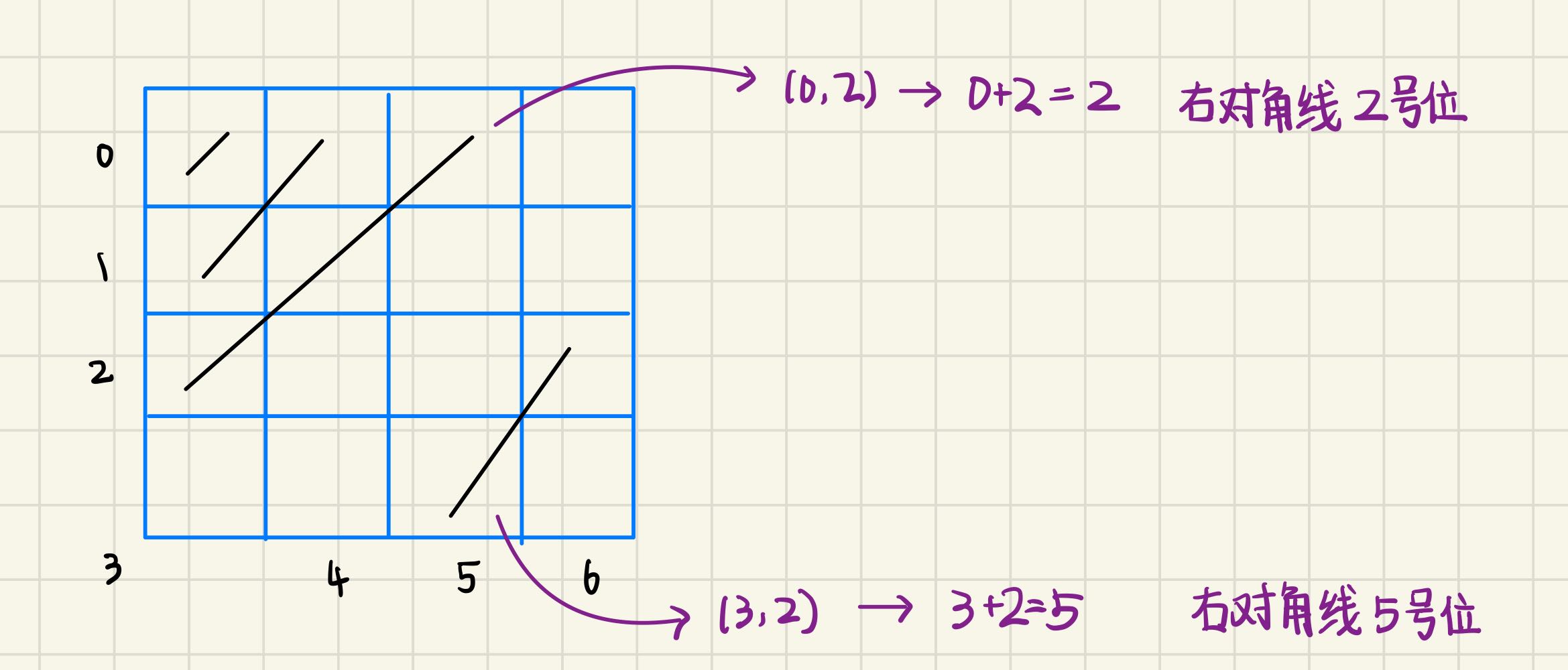
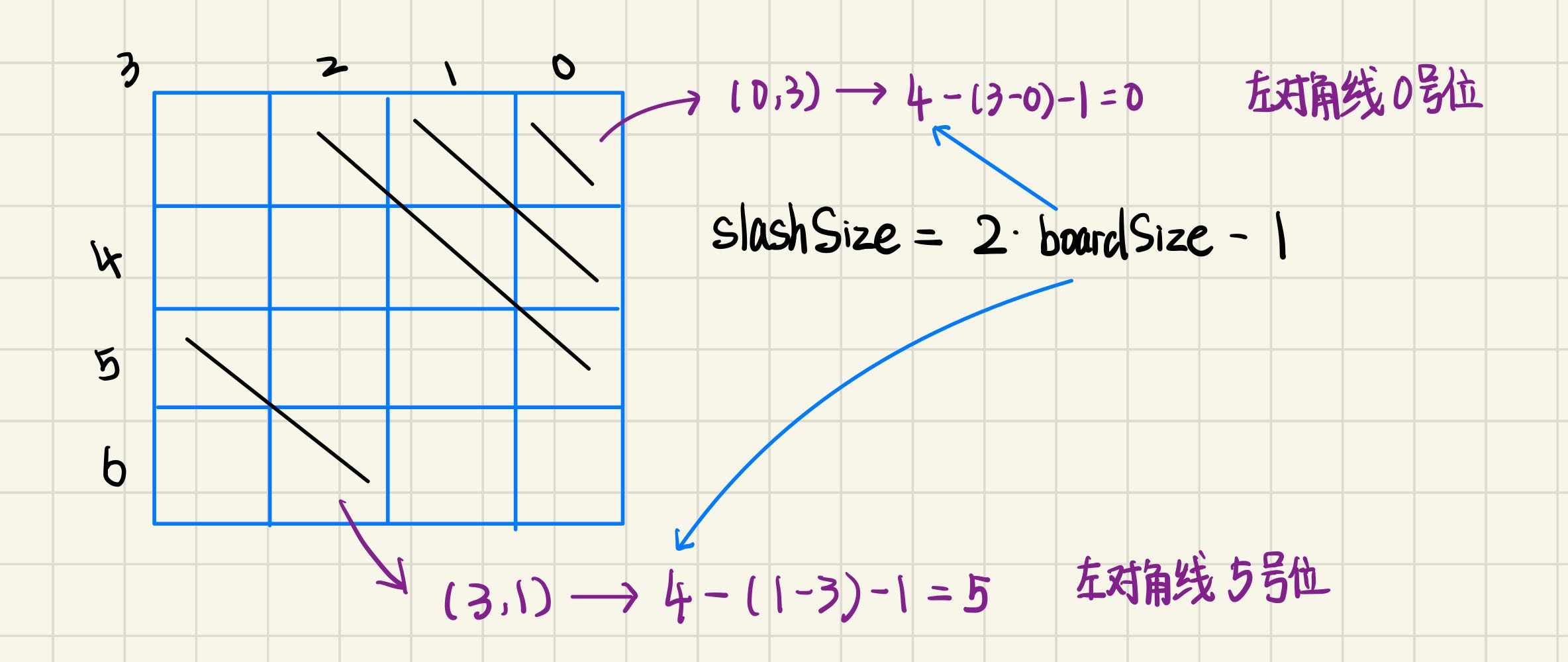
class MarkSolution
{
public:
    vector<bool> column, leftSlash, rightSlash;
    vector<vector<string>> result;
    vector<string> board;
    vector<vector<string>> solveNQueens(int n)
    {
        // 初始化列
        column = vector<bool>(n, true);
        // 初始化左对角线和右对角线
        leftSlash = rightSlash = vector<bool>(2 * n - 1, true);
        board = vector<string>(n, string(n, '.'));
        dfs(0);
        return result;
    }

    void dfs(int line)
    {
        int boardSize = board.size();
        if (line == boardSize)
            result.push_back(board);
        else
        {
            for (int i = 0; i < boardSize; i++)
            {
                int leftIndex = boardSize - line + i - 1;
                int rightIndex = line + i;
                // 判断是否能放置
                if (column[i] && rightSlash[rightIndex] && leftSlash[leftIndex])
                {
                    board[line][i] = 'Q';
                    column[i] = rightSlash[rightIndex] = leftSlash[leftIndex] = false;
                    dfs(line + 1);
                    board[line][i] = '.';
                    column[i] = rightSlash[rightIndex] = leftSlash[leftIndex] = true;
                }
            }
        }
    }
};

执行速率对比

广度优先搜索

看起来有点像层序遍历

走迷宫

因为LeetCode的题是收费的所以...

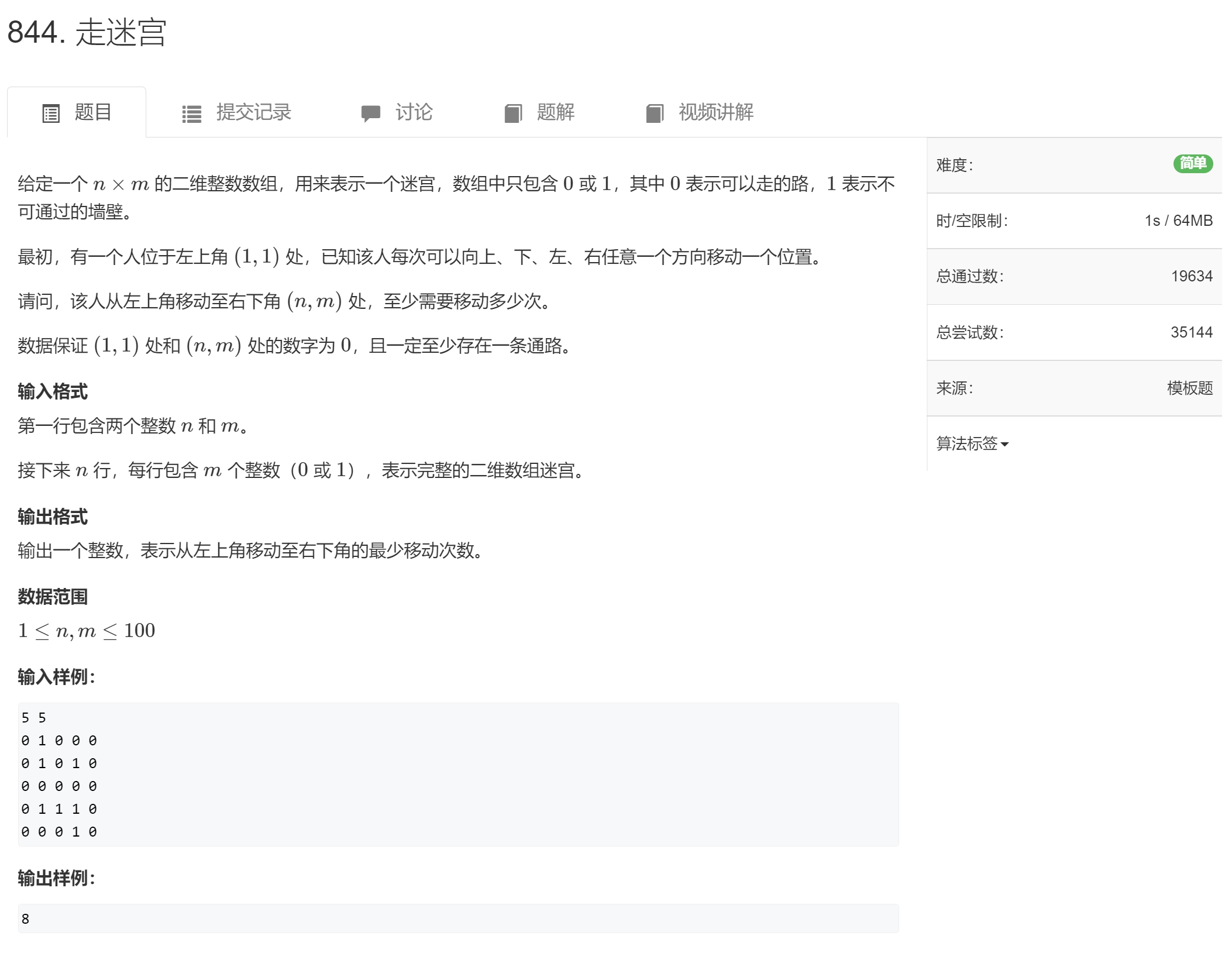
class Solution
{
public:
    int walkMaze(vector<vector<int>> maze)
    {
        // 初始化行 列
        int lineSize = maze.size();
        int columnSize = maze[0].size();
        // 初始化距离二维数组为-1
        vector<vector<int>> distance = vector<vector<int>>(lineSize, vector<int>(columnSize, -1));
        // 深度遍历队列
        queue<pair<int, int>> q;
        
        // 设置遍历的初始值 从左上角开始遍历
        distance[0][0] = 0;
        q.push(make_pair(0, 0));
        // 设置环顾方向 左 下 右 上
        int moveX[4] = {-1, 0, 1, 0};
        int moveY[4] = {0, -1, 0, 1};
        
        // 入队与出队处理
        while (!q.empty())
        {
            auto pos = q.front();
            q.pop();
            // 检测周围是否有元素能入队
            for (int i = 0; i < 4; i++)
            {
                int nextLineIndex = pos.first + moveY[i];
                int nextColumnIndex = pos.second + moveX[i];
                // 判断是否超出边界
                if (nextLineIndex >= 0 && nextColumnIndex >= 0 && nextLineIndex < lineSize && nextColumnIndex < columnSize)
                {
                    // 只走没走过的路 且 不被障碍物堵住
                    if (distance[nextLineIndex][nextColumnIndex] == -1 && maze[nextLineIndex][nextColumnIndex] != -1)
                    {
                        q.push(make_pair(nextLineIndex, nextColumnIndex));
                        distance[nextLineIndex][nextColumnIndex] = distance[pos.first][pos.second] + 1;
                    }
                }
            }
        }
        return distance[lineSize - 1][columnSize - 1];
    }
};

最短路问题

Floyd算法

时间复杂度为O(n^3)

• 首先应该建立最短路图，这是一个二维数组，初始值应该都是无限远。对角线的值是0，因为每个点到它们自身的距离是0。然后根据给的路径信息进行录入

  

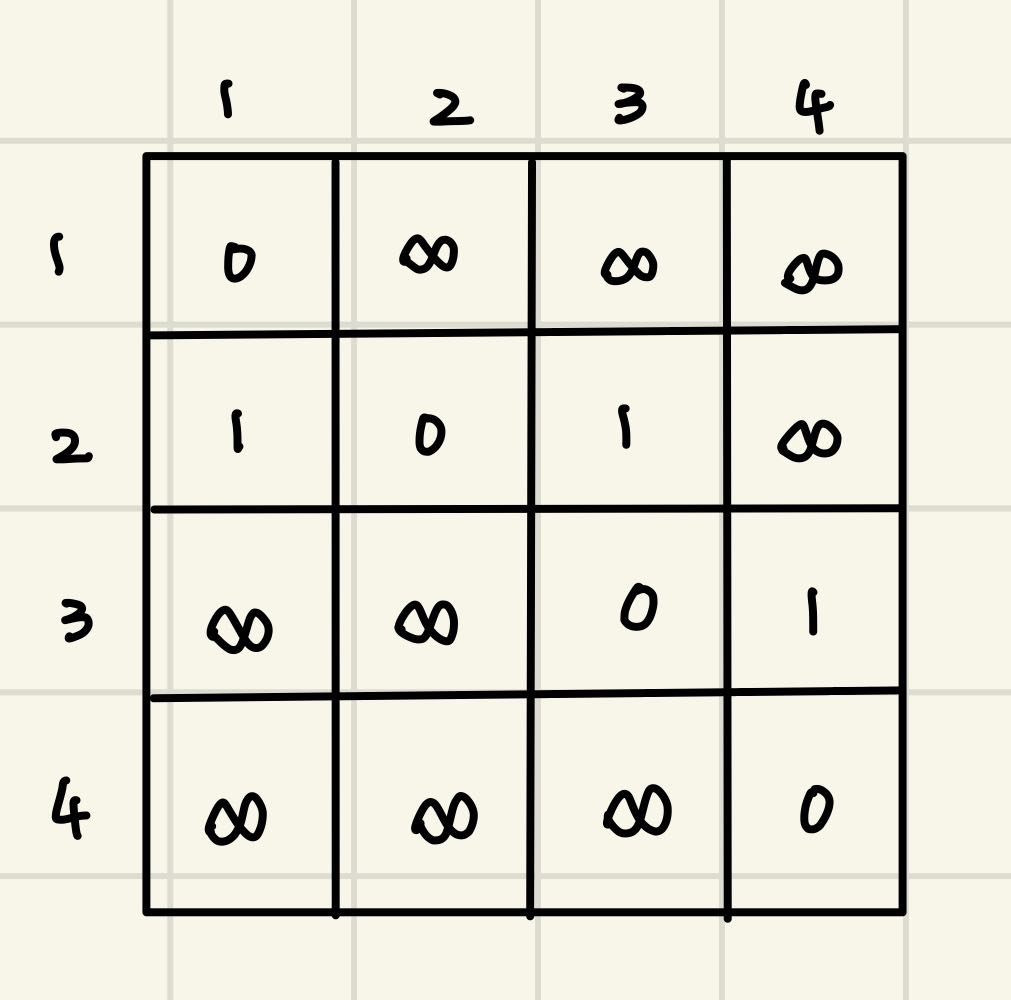
• 第二部遍历图，定一个点为桥梁（bridge），计算从一个点（i）经过桥梁到另一个点（j）的最短距离。综上，需要三次循环

• 最后选择第k个点，查看该点到其他各个点是否有不连通的情况，如果都能连通，那么求其中的最大值就是题目的答案

class Solution {
public:
    int networkDelayTime(vector<vector<int>>& times, int n, int k) {
        // 初始化图 默认最远距离为INT32_MAX
        std::vector<std::vector<long long>> graph(n + 1, std::vector<long long>(n + 1, INT32_MAX));
        // 每个点到它们自身的距离为0
        for (std::size_t i = 0; i < graph.size(); i++)
            graph[i][i] = 0;
        // 将联通数据写入图中
        for (const auto& time : times)
            graph[time[0]][time[1]] = time[2];

        // 以bridge作为桥梁
        for (std::size_t bridge = 1; bridge < graph.size(); bridge++)
        {
            // 查找i通过bridge到j的最短距离
            for (std::size_t i = 1; i < graph.size(); i++)
            {
                for (std::size_t j = 1; j < graph.size(); j++)
                {
                    graph[i][j] = std::min(graph[i][j], graph[i][bridge] + graph[bridge][j]);
                }
            }
        }

        long long result = 0;
        for (std::size_t index = 1; index < graph.size(); index++)
        {
            if (graph[k][index] == INT32_MAX)
                return -1;
            result = std::max(result, graph[k][index]);
        }
        return result;

    }
};

贪心（待完成）

其他（待完成）

C++中的cin和cout