DS博客作业05--树
1.思维导图

1.1.谈谈你对树结构的认识及学习体会。
1.学完树的内容再回顾树与之前所所学的不同的是数结构是一种非线性结构,常见的树形结构是树和二叉树,在树中主要是一个结点对应多个结点从而能表示层次结构的数据。二叉树的建立于销毁,查找孩子结点,求二叉树的高度。其次有二叉树的先、中后序遍历、层次遍历,层次遍历概念很简单,主要是实现。线索二叉树就是把二叉树连接线索方便查找结点的父母亲,和孩子结点。哈夫曼树是总权值最小的二叉树,在开始时会把哈夫曼树画错,理解为只要画为书上的样例即可,发现权值不是最小的,后来才慢慢理清怎么画哈夫曼树。
2.PTA实验作业
2.1 题目1:中序输出度为1的结点
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
typedef char ElemType;
typedef struct BiTNode
{
ElemType data;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
BiTree Create();/* 细节在此不表 */
void InorderPrintNodes( BiTree T);
int main()
{
BiTree T = Create();
printf("Nodes are:");
InorderPrintNodes(T);
return 0;
}
/* 你的代码将被嵌在这里 */
2.1.1设计思路
if(树.空) return ;
中序遍历左子树;
if(左孩子or右孩子有一方不为空)
{
printf(输出根节点)
}
中序遍历右孩子;
2.1.2代码截图

2.1.3本题PTA提交列表说明

- Q1:部分正确
- A1:说明空树的情况时正确,检查代码发现左右孩子树其中一个不为空的时候输出根节点,改过来即可。
2.2.题目2:求二叉树高度
2.2.1设计思路
if (树==NULL) return 0;
定义结构体变量 p=BT,数组 a[100];
定义变量 front=-1,rear=-1,last=0,level=0;
a[++rear]=p;
while front小于rear
{
取结点p=a[++front];
if(左结点)
{ 左孩子存入a[++rear]}
if(右结点)
{ 左孩子存入a[++rear]}
if(front==last)
{
高度++;}
over
2.2.2代码截图
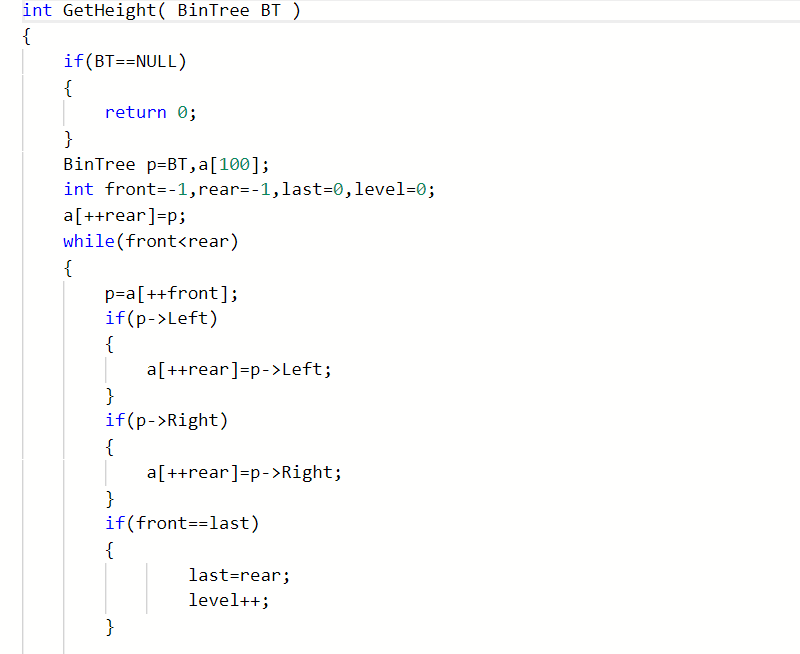
2.2.3本题PTA提交列表说明

2.3 题目3:jmu-ds-二叉树层次遍历
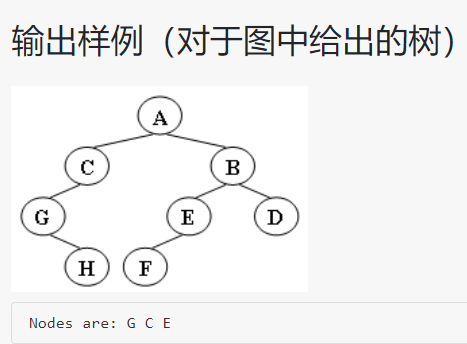
层次遍历树中所有节点。 输入一行字符串表示二叉树的顺序存储结构,比如字符串“#ABCD#EF#G##H##I”,#代表空节点。第一个#不使用。
代表二叉树如图所示:

输入格式:
输入一行字符串,第一个字符#开始。空节点用#表示。
输出格式:
层次遍历二叉树,输出的节点间要求空格隔开,最后一个节点尾部无空格。若二叉树为空,则输出NULL
输入样例:
ABCD#EF#G##H##I
输出样例:
A B C D E F G H I
2.3.1设计思路
省略创建树函数.......
void LeverOrder( BTree T )
{
定义结构体 p,定义qu[MaxSize];
定义front =-1,rear=-1,flag=0;
qu[rear++]赋值T;
if(T!==NULL)
{
while(front!=rear)
{
if(!flag&&p->data!=NULL)
else if //控制输出
if(左孩子不为空)
进入数组 =左孩子;
if(右孩子不为空)
进入数组 =右孩子;
}
}
if(遍历完,flag=0) 则为空树
2.3.2代码截图

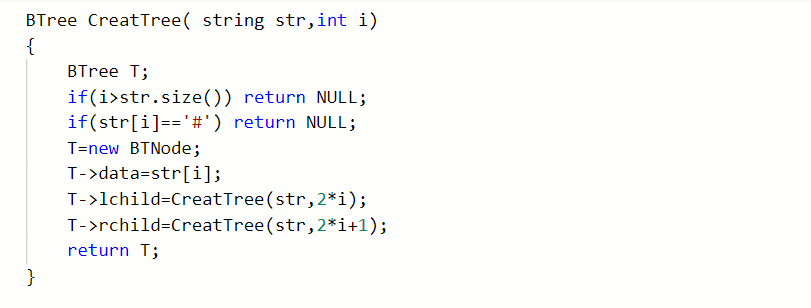


2.3.3本题PTA提交列表说明
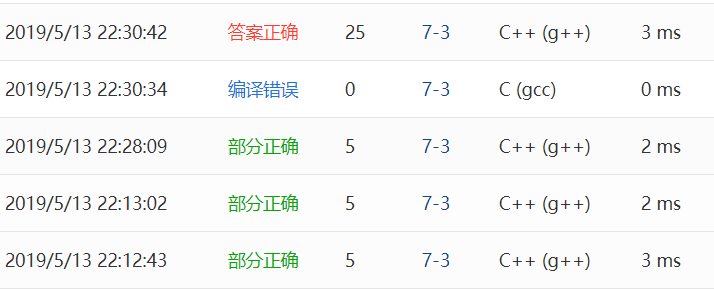
- Q1:部分正确
- A1:只对了空树的情况,后来发现没有忘了添上rear=(rear+1)%MaxSize,导致在取值时错误。
3、阅读代码
3.1 题目
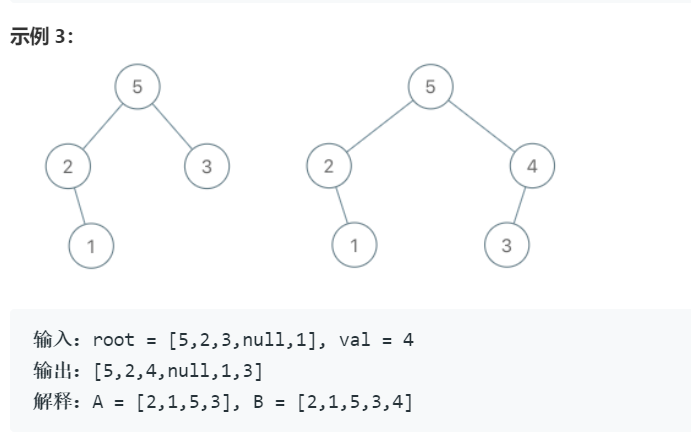
最大树定义:一个树,其中每个节点的值都大于其子树中的任何其他值。
给出最大树的根节点 root。
就像之前的问题那样,给定的树是从表 A(root = Construct(A))递归地使用下述 Construct(A) 例程构造的:
如果 A 为空,返回 null
否则,令 A[i] 作为 A 的最大元素。创建一个值为 A[i] 的根节点 root
root 的左子树将被构建为 Construct([A[0], A[1], ..., A[i-1]])
root 的右子树将被构建为 Construct([A[i+1], A[i+2], ..., A[A.length - 1]])
返回 root
请注意,我们没有直接给定 A,只有一个根节点 root = Construct(A).
假设 B 是 A 的副本,并附加值 val。保证 B 中的值是不同的。
返回 Construct(B)。


3.2 解题思路
思路一:通过中序遍历获取所有点的值,然后将val插入到数组,再通过调用之前问题的函数即可。
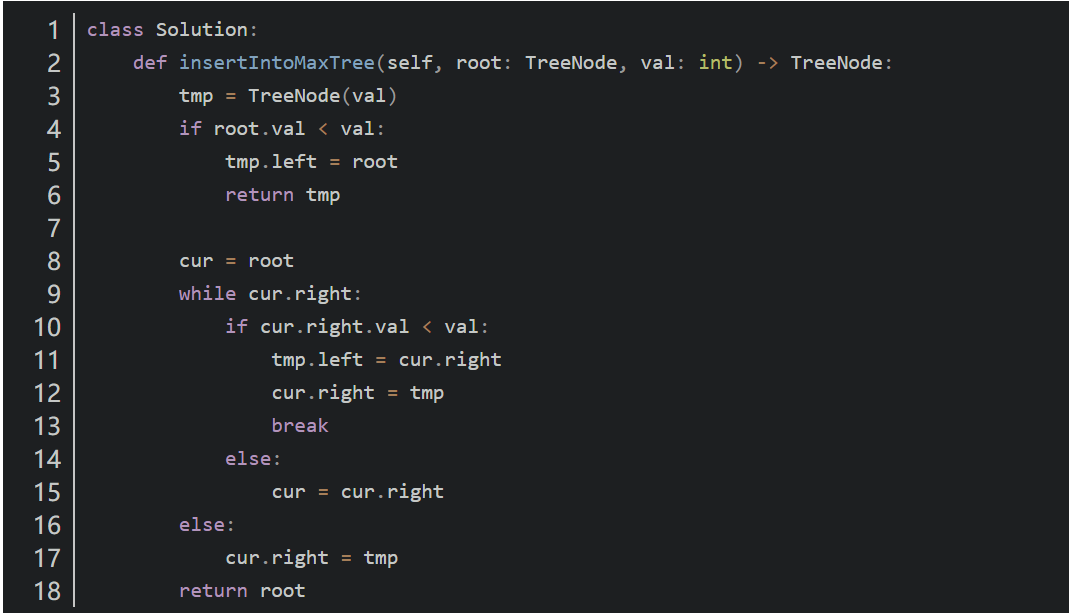
思路二:找右子树中大于插入元素的第一个节点的位置,然后将当前节点插入其右侧,而小于插入元素的节点,现在就变成插在其左侧。
3.3 代码截图
- 代码一:
![]()
- 代码二:
![]()
- 代码三:
![]()
3.4 学习体会
这道题的思路好理解,就是一个查找插入的过程,代码一比较好实现是用数组来操作,不过其他方法的思路和代码一是差不多的也是查找插入的过程,代码相比较比方法一少些,时间和空间的复杂度代码一的不是很高,代码二三相比一如果有左子树的数据很多多而右子树的数据很少少,用代码二三处理要更好一些。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号