在开放源码的KLSudoku标准数独游戏里,实现了X-Chain和Forcing-Chain的逻辑解法,有朋友询问是如何实现的,特在这里说明一下我的思路。 源码可以从solver.cs里看到。
关于X-Chain和Forcing-Chain解法的说明,可以从数独百科网站查阅:
http://www.sudopedia.org/wiki/X-Chain
A X-Chain is a single-digit solving technique which uses a chain consisting of links that alternate between strong links and weak links, with the starting and ending link being strong. In other words, the chain involves an even number of cells having the target digit as a candidate. The target digit can be eliminated from any cell that is seen by both ends of the X-Chain.
X-Chain解法的链里只涉及到一个候选数,X-Chain是由强链接和弱链接交替连接形成的,强链接意味着在同一个行/列/快里,只有两个数格包含有这个候选数,而弱连接则表示有三个或者三个以上的数格可以包含这个候选数。
对于强连接而言,当前一个几点为真,则下一个节点必然为假,并且如果前一个节点为假,下一个节点就必然为真(这在链的形成中是关键)http://www.sudopedia.org/wiki/Strong_link
对于弱连接而言,只能有一个推断——当前一个节点为真时,下一个节点必然为假。http://www.sudopedia.org/wiki/Weak_link
当强连接和弱连接交替组成的链存在的时候,就可以从第一个节点的真假推断出后面节点的真假。从而就可以对同时与X-Chain里的节点形成连接的一些节点做出推断。
显然,这些可以得到推断的节点也是X-Chain里的一部分,那么如何得到推断呢?
假设我们正在遍历一个X-Chain链,当我们发现下一个节点已经在遍历过程中经历过的时候,就可能可以得到推断了:(弱链首即强链尾,强链首即弱链尾)
- 假设当前节点是弱链尾,如果其与链里任意一个强链首有强连接,则该强链首的候选数就是正确的候选数(假设它不是会得出当前节点也不是!)
- 假设当前节点是强链尾,如果其与链里任意一个弱链首有连接(强弱均可),则弱链首节点的候选数排除(假设它为真会得到当前节点也真!)
- 对于当前节点是弱链尾,下一个节点是强链尾节点的情况,无法得出推断,这个X-Chain到此终止,可以回溯寻找别的X-Chain
- 对于当前节点是强链尾,下一个节点是弱链尾的情况,也无法得出推断。此时同样需要回溯去寻找其他的X-Chain
如果我们用=>表示强链,->表示弱链,举个例子:
A => B -> C => D -> E => F ->G
对于第一种情况:如果G与A有强连接,则有这样的推断:
- 如果A为真,G为假(因为他们有强连接)
- 如果A为假,则B为真,C为假,D为真,E为假,F为真,得出G为假
- 无论A取值如何,G都为假,而G与A是强连接,所以A必然为真
而如果G与A无强连接的话,则不能得出上面的推论。因为当A为假,G为假在A与G只是弱连接的时候,是无法得出矛盾推论的。
对于第二种情况:如果H与G是强连接,H与B存在连接,则H是强链尾,B是弱链首,得出B不可能为真,推理过程如下:
- 假设B为真,则C为假,D为真,E为假,F为真,G为假,而G与H强连接,则H为真,而H与B存在连接,所以B要为假,这显然与起始假设矛盾
这是X-Chain的例子:
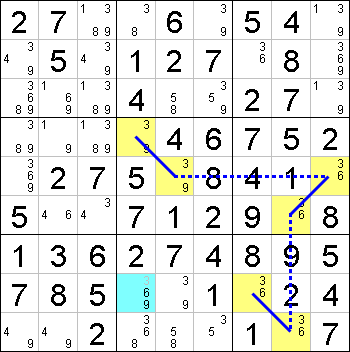
这个图就是第一种推断:
- 如果r4c4=3 -> r8c4!=3
- r4c4!=3 => r5c5=3 -> r5c9!=3 => r6c8=3 -> r9c8!=3 => r8c7=3 -> r8c4!=3
- 无论r4c4如何取值,都可以得出r8c4!=3,所以r8c4的3可以排除
这是另外一个X-Chain的例子


说完了X-Chain,再说说Forcing-Chain,Forcing-Chain的说明:http://www.sudopedia.org/wiki/Forcing_Chain
如何利用Forcing-Chain解题呢?
其实和X-Chain是基本一样的,但是Chain里的节点,不再是所有候选数都相同了。
那么不同的候选数如何形成链呢?
答案就是在相同的数格内,不同的候选数之间可以形成链:
- 如果数格内只有两个候选数,那么就形成强链(符合A真B假,A假B真的推断)
- 如果数格内有三个候选数,那么就形成弱链(符合A真B假,A假不能得出B的推断)
下面就是一个例子:

在r9c9的2和6就是一个同数格的弱连接,图里的Chain是这样的:
G2=2 -> I1=2 => I9=2 -> I9=6 => H7=6 -> H2=6 => G2=6 -> G2=2
所以倘若Chain的第一个节点G2=2成立,就会推断出最后一个节点G2=2不成立,形成矛盾,所以G2数格可以排除2!




