leetcode(23)贪心系列题目

455. 分发饼干

从小的饼干开始发，注意从0开始如果饼干大于第0个胃口，则res+1，即满足了1个胃口

class Solution:
    def findContentChildren(self, g: List[int], s: List[int]) -> int:
        g.sort()
        s.sort()
        res = 0
        for j in range(len(s)):
            if res < len(g) and s[j] >= g[res]:
                res += 1
        return res

376. 摆动序列

贪心，记录前一个差与当前差，若两者乘积<=0，且当前差不等于0，则序列长度+1，前一个差被赋值为当前差

class Solution:
    def wiggleMaxLength(self, nums: List[int]) -> int:
        preC, curC, res = 0, 0, 1
        for i in range(1, len(nums)):
            curC = nums[i] - nums[i - 1]
            if curC * preC <= 0 and curC != 0:
                res += 1
                preC = curC
        return res

53. 最大子数组和

这道题目的思想是： 走完这一生 如果我和你在一起会变得更好，那我们就在一起，否则我就丢下你。 我回顾我最光辉的时刻就是和不同人在一起，变得更好的最长连续时刻

如果前边累加后还不如自己本身大，那就把前边的都扔掉，从此自己本身重新开始累加。

如果加入当前元素后的curMax<没有加之前的res,则不会添加当前元素

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        res = float('-inf')
        cur = 0
        for i in range(len(nums)):
            cur = max(nums[i], nums[i] + cur)
            res = max(res, cur)
        return res

122. 买卖股票的最佳时机 II

把利润分解为每天为单位的维度，而不是从0天到第3天整体去考虑

那么根据prices可以得到每天的利润序列：(prices[i] - prices[i - 1]).....(prices[1] - prices[0])。

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        res = 0
        for i in range(1, len(prices)):
            res += max(0, prices[i] - prices[i - 1])
        return res

55. 跳跃游戏

用cover记录当前覆盖的可跳到的位置
问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点

每次移动取最大跳跃步数（得到最大的覆盖范围），每移动一个单位，就更新最大覆盖范围。

class Solution:
    def canJump(self, nums: List[int]) -> bool:
        cover = i = 0
        if len(nums) == 1:return True
        while i <= cover:
            cover = max(cover, nums[i] + i)
            if cover >= len(nums) - 1:
                return True
            i += 1
        return False

45. 跳跃游戏 II

记录能覆盖的最大距离，当遍历到覆盖的最后一个时，要多一跳

class Solution:
    def jump(self, nums: List[int]) -> int:
        max_cov = end = res = 0
        for i in range(len(nums) - 1):
            max_cov = max(max_cov, nums[i] + i)
            if i == end:
                end = max_cov
                res += 1
        return res

1005. K 次取反后最大化的数组和

将nums按绝对值从大到小排列，把负数全部转正之后，最后k还有剩就只转最后一个数

class Solution:
    def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:
        nums = sorted(nums, key = abs, reverse = True)
        for i in range(len(nums)):
            if nums[i] < 0 and k > 0:
                nums[i] *= -1
                k -= 1
        if k > 0:
            nums[-1] *= (-1)**k
        return sum(nums)

134. 加油站

首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈，说明 各个站点的加油站 剩油量rest[i]相加一定是大于等于零的。

每个加油站的剩余量rest[i]为gas[i] - cost[i]。

i从0开始累加rest[i]，和记为curSum，一旦curSum小于零，说明[0, i]区间都不能作为起始位置，起始位置从i+1算起，再从0计算curSum。

class Solution:
    def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
        curSum = 0
        totalSum = 0
        start = 0
        for i in range(len(gas)):
            curSum += gas[i] - cost[i]
            totalSum += gas[i] - cost[i]
            if curSum < 0:
                curSum = 0
                start = i + 1
        if totalSum < 0:return -1
        return start

135. 分发糖果

采用了两次贪心的策略：

• 一次是从左到右遍历，只比较右边孩子评分比左边大的情况。
• 一次是从右到左遍历，只比较左边孩子评分比右边大的情况。

最后取最大值，即糖果数量要多于左右两边评分较大的孩子
这样从局部最优推出了全局最优，即：相邻的孩子中，评分高的孩子获得更多的糖果。

class Solution:
    def candy(self, ratings: List[int]) -> int:
        n = len(ratings)
        left = [1] * n
        right = [1] * n
        for i in range(1, n):
            if ratings[i] > ratings[i - 1]:
                left[i] = left[i - 1] + 1
        for i in range(n - 2, -1, -1):
            if ratings[i] > ratings[i + 1]:
                right[i] = right[i + 1] + 1
        res = 0
        for i in range(n):
            res += max(left[i], right[i])
        return res

860. 柠檬水找零

优先消耗10美元，因为5美元的找零用处更大，能多留着就多留着

class Solution:
    def lemonadeChange(self, bills: List[int]) -> bool:
        five, ten = 0, 0
        for bill in bills:
            if bill == 5:
                five += 1
            elif bill == 10:
                if five == 0:
                    return False
                else:
                    five -= 1
                    ten += 1
            else:
                if ten > 0 and five > 0:
                    ten -= 1
                    five -= 1
                elif five > 2:
                    five -= 3
                else:
                    return False
        return True

406. 根据身高重建队列

首先对people进行排序，按照people的元素 h 降序排序，再按照people的元素 k 升序排序。最后再按k值插入。

插入的过程：

• 插入[7,0]：[[7,0]]
• 插入[7,1]：[[7,0],[7,1]]
• 插入[6,1]：[[7,0],[6,1],[7,1]]
• 插入[5,0]：[[5,0],[7,0],[6,1],[7,1]]
• 插入[5,2]：[[5,0],[7,0],[5,2],[6,1],[7,1]]
• 插入[4,4]：[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]

class Solution:
    def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:
        # 先按第一列降序，再按第二列升序排列
        people.sort(key = lambda x:(-x[0],x[1]))
        # print(people)
        que = []
        for p in people:
            # print(que)
            # 按第2列的序号插到对应的位置，例如[4,4]就放在索引为4的位置
            # 但之前第1列比较大的就会被挤到后面去，例如[5,0],[7,0]
            que.insert(p[1],p)
        return que

452. 用最少数量的箭引爆气球

能引爆的范围即覆盖范围

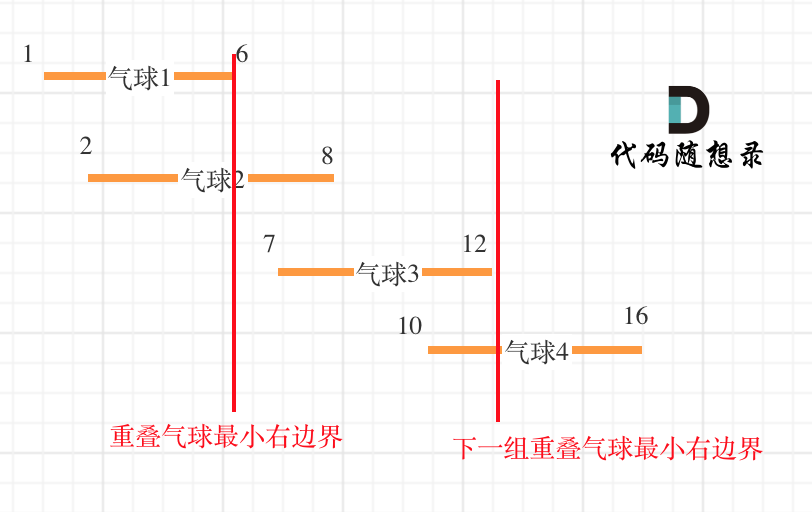
判断重叠：当前范围的左边界是否位于上一个范围的左右边界之间

• 若重叠了，重叠气球中右边界的最小值一定需要一个弓箭，因此更新当前范围的右边界为两个右边界中的最小值
• 若没有重叠则需要增加一支箭

第一组重叠气球，需要一个箭。然后气球3的左边界大于了第一组重叠气球的最小右边界，说明没有继续重叠，所以再需要一支箭来射气球3了。

class Solution:
    def findMinArrowShots(self, points: List[List[int]]) -> int:
        if len(points) == 1: return 1
        points.sort(key = lambda x:(x[0]))
        print(points)
        res = 1
        for i in range(1, len(points)):
            if points[i][0] <= points[i - 1][1]:
                # 有重叠部分
                points[i][1] = min(points[i][1], points[i - 1][1])
            else:
                # 没有重叠，需要增加一支箭
                res += 1
        return res

435. 无重叠区间

• 若重叠了，更新当前区间的右边界为两个右边界的最小值，这样删除区间的个数就是最小的
• 注意初始化res = 0而不是1 ，因为如果不重叠就不用删，452. 用最少数量的箭引爆气球则是不重叠就需要一支箭

class Solution:
    def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
        if len(intervals) == 1:return 0
        intervals.sort(key = lambda x:(x[0]))
        # print(intervals)
        res = 0
        for i in range(1, len(intervals)):
            if intervals[i][0] < intervals[i - 1][1]:
                intervals[i][1] = min(intervals[i][1], intervals[i - 1][1])
                res += 1
        return res

763. 划分字母区间

首先用字典或列表存每个字母的最右边界，再遍历的时候，如果没有超出都是在同一段中

class Solution:
    def partitionLabels(self, s: str) -> List[int]:
        # map_ = dict()  # 用字典记录
        hash_ = [0] * 26  # 用列表记录性能更优
        for i in range(len(s)):
            # map_[s[i]] = i
            hash_[ord(s[i]) - ord('a')] = i
        # print(map_)
        # print(hash_)
        res = []
        left, right = 0, 0
        for i in range(len(s)):
            # right = max(right, map_[s[i]])
            right = max(right, hash_[ord(s[i]) - ord('a')])
            if i == right:
                res.append(right - left + 1)
                left = right + 1
        return res

56. 合并区间

与存入结果集的最后一个区间比较，性能更优

class Solution:
    def merge(self, intervals: List[List[int]]) -> List[List[int]]:
        if len(intervals) == 1:return intervals
        intervals.sort(key = lambda x:(x[0]))
        # print(intervals)
        res = [intervals[0]]
        for i in range(1, len(intervals)):
            last = res[-1]  # 已经存入结果集的最后一个区间
            if intervals[i][0] <= last[1]:  # 与前一个区间有重叠
                # 更新最后一个区间的右边界
                last[1] = max(last[1], intervals[i][1])                
            else:  # 与前一个区间没有重叠
                res.append([intervals[i][0], intervals[i][1]])
        return res

738. 单调递增的数字

转成list处理每一位数值，若num[i] < num[i - 1]则i后面的数值都是9，并且num[i - 1] - 1退位

class Solution:
    def monotoneIncreasingDigits(self, n: int) -> int:
        num = list(str(n))
        for i in range(len(num)-1,0,-1):
            if int(num[i]) < int(num[i - 1]):
                num[i:] = '9' * (len(num) - i)
                num[i - 1] = str(int(num[i - 1]) - 1)
        return int(''.join(num))

714. 买卖股票的最佳时机含手续费

分三种情况，买入，卖出（可能在收获利润的区间里，因此不能重复计算fee），不买也不卖

class Solution:
    def maxProfit(self, prices: List[int], fee: int) -> int:
        res = 0
        min_pri = prices[0]
        for i in range(1, len(prices)):
            if prices[i] < min_pri:
                # 买入，但是没有算手续费
                min_pri = prices[i]
            elif prices[i] >= min_pri and prices[i] <= min_pri + fee:
                # 两边都有=
                # 保持上一个状态，不买也不卖
                continue
            else:
                # 卖出，在此时算手续费，因为可能买卖多次但只算一次手续费
                res += prices[i] - min_pri - fee
                min_pri = prices[i] - fee  # 注意-fee，下一次计算利润就不会重复出手续费
        return res

968. 监控二叉树

头结点不放摄像头也就省下一个摄像头， 叶子节点不放摄像头省下了的摄像头数量是指数级别的。

所以要从下往上看，局部最优：让叶子节点的父节点安摄像头，所用摄像头最少，整体最优：全部摄像头数量所用最少！

在二叉树中从下向上推导可以使用后序遍历。

• 情况1.该节点有摄像头：0
• 情况2.该节点无摄像头
  • 2.1该节点被覆盖：1
  • 2.2该节点无覆盖：2

class Solution:
    def minCameraCover(self, root: Optional[TreeNode]) -> int:
        # 0:有摄像头
        # 1:覆盖
        # 2:无覆盖
        res = 0
        def traversal(cur):
            nonlocal res
            # 空节点只能保证自己是覆盖的
            if not cur:return 1
            left = traversal(cur.left)
            right = traversal(cur.right)

            if left == 1 and right == 1:
                return 2
            elif left == 2 or right == 2:
                res += 1
                return 0
            elif left == 0 or right == 0:
                return 1
            
        if traversal(root) == 2:
            res += 1
        return res

6091. 划分数组使最大差为 K

注意：不用输出拆分的结果，而且子序列内部只要关注最大值和最小值即可，也不用关心元素的顺序。所以直接排序+贪心
步骤：
1.排序，并初始化最大最小值
2.更新最大最小值
3.如果当前子序列的最大最小值之差大于k，则需要再用一个数组来存后面的数
4.更新最大最小值为下一个子序列的值

class Solution:
    def partitionArray(self, nums: List[int], k: int) -> int:
        nums.sort()  # 步骤1
        maxv, minv = -inf, inf
        res = 1
        for i in range(len(nums)):
            minv = min(minv, nums[i])  # 步骤2
            maxv = max(maxv, nums[i])
            if minv < inf and maxv - minv > k:
                res += 1  # 步骤3
                maxv, minv = nums[i], nums[i]  # 步骤4
        return res

1710. 卡车上的最大单元数

排序+贪心

class Solution:
    def maximumUnits(self, boxTypes: List[List[int]], truckSize: int) -> int:
        boxTypes.sort(key = lambda x:x[1], reverse = True)
        i = res = 0
        while truckSize > 0 and i < len(boxTypes):
            res += boxTypes[i][1] * min(boxTypes[i][0], truckSize)
            truckSize -= boxTypes[i][0]
            i += 1
        return res