画出 sklearn 中支持向量机分类函数 SVC 的分类结果图（Draw the classification result graph of the svm classification function SVC in sklearn library）
在最近的学习中，看到代码中展示了如何画出支持向量机分类结果的决策面、最大间隙面和支持向量，即确定用支持向量机分类函数 SVC 进行分类后得到分类超平面和间隙面函数以及支持向量坐标的方法，分享给大家~
1. 训练 svm 分类器 SVC 代码
1 from sklearn import svm
2 import numpy as np
3 from matplotlib import pyplot as plt
4 plt.ion()
5
6 # 随机生成两组数据，并通过(-2,2)距离调整为明显的0/1两类
7 # 本来是分布相同的两个函数，通过一定的操作将它们分离开来，具体的操作是对x,y的值进行左右上下移动
8 data = np.r_[np.random.randn(30, 2) - [-2, 2], np.random.randn(30, 2) + [-2, 2]]
9 # 设置标签，前面30个数据标签是0，后面30个数据标签是1
10 target = [0] * 30 + [1] * 30
11
12 # 建立SVC模型
13 clf = svm.SVC(kernel='linear')
14 clf.fit(data, target)
15
16 # 显示结果
17 w = clf.coef_[0]
18 a = -w[0] / w[1]
19 print("参数w: ", w)
20 print("参数a: ", a)
21 print("支持向量: ", clf.support_vectors_)
22
23 # 使用结果参数生成分类线
24 xx = np.linspace(-5, 5)
25 yy = a * xx - (clf.intercept_[0] / w[1])
26
27 # 绘制穿过正支持向量的虚线
28 b = clf.support_vectors_[0]
29 # 已经斜率为a，又经过点(b[0], b[1])就可以得到以下直线方程
30 yy_Neg = a * xx + (b[1] - a * b[0])
31
32 # 绘制穿过负支持向量的虚线
33 b = clf.support_vectors_[-1]
34 yy_Pos = a * xx + (b[1] - a * b[0])
35
36 # 绘制黑色实线
37 plt.plot(xx, yy, 'r-')
38 # 绘制黑色虚线
39 plt.plot(xx, yy_Neg, 'k--')
40 plt.plot(xx, yy_Pos, 'k--')
41
42 # 绘制样本散点图
43 plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1])
44 plt.scatter(data[:, 0], data[:, 1], c=target, cmap=plt.cm.coolwarm)
45
46 plt.xlabel("X")
47 plt.ylabel("Y")
48 plt.title("Support Vector Classification")
49
50 pass
代码运行结果：
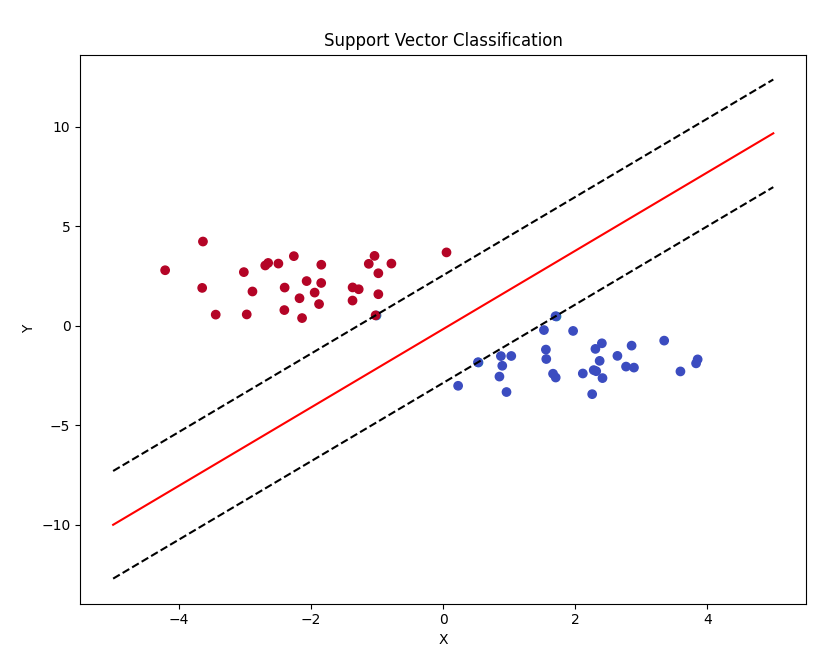
结果分析和说明：
（1）分类线的生成是从 clf.coef_ 和 clf.intercept_ 中获取权重和截距的结果，其中，yy = a * xx - (clf.intercept_[0] / w[1]) 计算公式由来根据 这篇文章 中的方程。
即通过矩阵求解 wx+b=0，矩阵计算形式即
得到。 图中的坐标中，一个坐标轴是 x1，一个坐标轴是 x2，但是在本代码中，一个坐标轴是 x，一个坐标轴是 y，所以就是直线方程就是 
，这就是第 25 行代码的由来。注意，这里为什么是 wx + b = 0，因为在超平面的一侧 y>0 ，在超平面的另一侧 y<0 ，而在超平面上就是 y=0 。
（2）图中的支持向量有3个，可以从支持向量返回的结果是 3 行 2 列的数据可知，这个和结果放大图中的结果一致，即上面第二张图中在直线上的点（图中用绿色的圈圈出）有3个，所以再次证明支持向量确实是3个。
（3）间隙线的由来：分类线是直线，所以满足直线方程 y=kx+b，根据 25 行，可知 k=a，b= - (clf.intercept_[0] / w[1])，因为间隙线和分类线平行，所以可知间隙线的斜率 k 也是 a，那么就剩下截距 b 的计算，又已知间隙线过支持向量，即已知直线的斜率和通过直线的一个点，那么就可以确定直线的方程，具体计算可以看下图。
以上就是 30 行代码的由来，同理可以知道 34 行代码的由来。
2. SVC 预测结果代码
1 from sklearn import svm
2
3 # 样本特征
4 x = [[2, 0], [1, 1], [2, 3]]
5 # 样本的标签
6 y = [0, 0, 1]
7
8 # 建立SVC分类器
9 clf = svm.SVC(kernel='linear')
10 # 训练模型
11 clf.fit(x, y)
12 print(clf)
13
14 # 获得支持向量
15 print(clf.support_vectors_)
16
17 # 获得支持向量点在原数据中的下标
18 print(clf.support_)
19
20 # 获得每个类支持向量的个数
21 print(clf.n_support_)
22
23 # 预测(2,0)的类别
24 print(clf.predict([[2, 0]]))
代码运行结果：
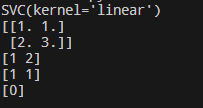
以下是我在已知支持向量的情况下，手动计算出分类线的过程，感兴趣的小伙伴可以看下
以上代码主要来自 《Python机器学习——原理、算法及案例实战-微课视频版》——清华大学出版社 刘艳、韩龙哲、李沫沫 编著 ISBN：9787302590026 书中第九章节——支持向量机 中例子。
