深度学习导论知识——最大似然估计法（Introductory Knowledge of Deep Learning - Maximum Likelihood Estimation）
最大似然估计法，是学习深度学习不可缺少的知识，在 《深度学习全书 公式+推导+代码+TensorFlow全程案例》—— 洪锦魁主编 清华大学出版社 ISBN 978-7-302-61030-4 这本书中看到了相关知识，简洁明了，分享给大家~
1. 知识点
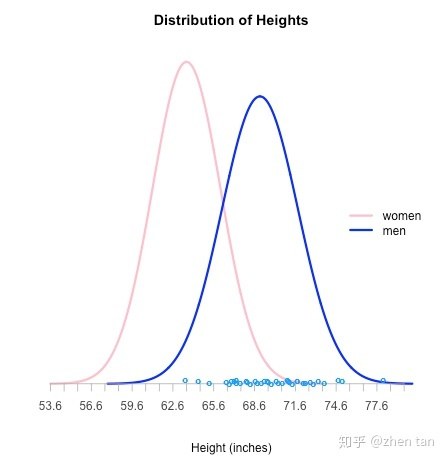
最大似然估计法（MLE, Maximum Likelihood Estimation）是估计参数值的方法，目标是找到一个参数值，使出现目前事件的概率最大。如下图所示，曲线是四个可能的正态概率分布（平均数/变异数不同），我们希望利用最大似然估计法找到最适配（Fit）的一个正态概率分布。
其中，样本点就是事件可能产生的取值，看下图会更加清楚，如采集到一些男性身高的样本点（下图中的蓝色点），由点的疏密程度对应着事件发生的概率的大小，由此可以得到蓝色的曲线是男性身高的概率分布曲线。此外，曲线高度越高，事件发生的概率就越大，由此可以看到密集的样本点发生的概率比稀疏的样本点发生的概率大。
2. 公式推导
下面使用最大似然估计法求算正态分布的参数 μ 及 δ。
（1）正态分布
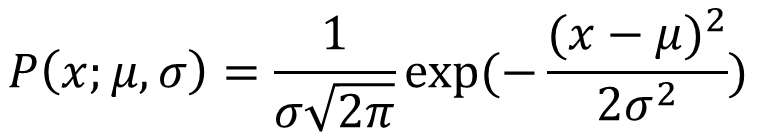（公式1）
（2）假设来自正态分布的多个样本相互独立，那么，联合概率就等于个别的概率相乘。即
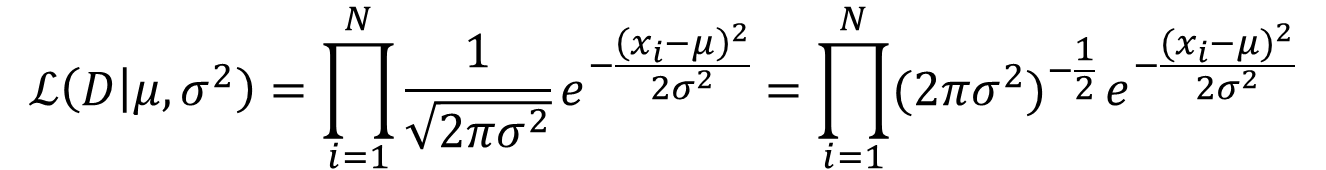（公式2）
（3）目标是求取参数值 μ 及 δ，最大化概率值，即最大化目标函数。即
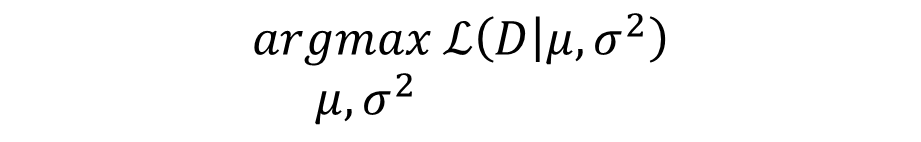（公式3）
（4）N 个样本概率全部相乘，不易计算，通常我们会取对数，变成一次方，所有的概率值取对数后，大小顺序并不会改变。即
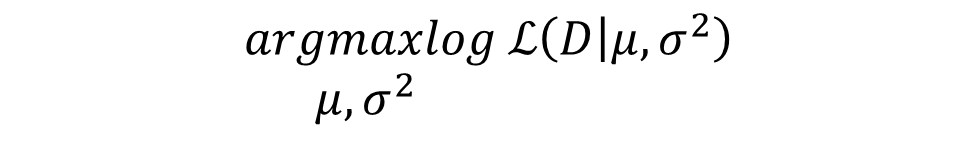（公式4）
（5）取对数后，化简为
（公式5）
（6）对 μ 及 δ 分别偏微分，得
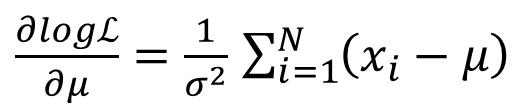（公式6）
（公式7）
（7）一阶导数为0时，有最大值，得到目标函数最大值下得 μ 及 δ。所以，使用最大似然估计法算出的 μ 及 δ 就如同我们常见的公式。有
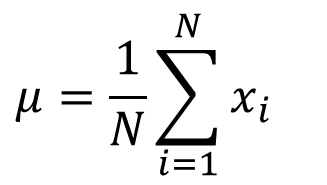（公式8）
（公式9）
3. 程序代码
范例1：如果样本点 x=1，计算来自正态分布 N(0, 1) 的概率，即已知正态分布的概率密度函数，求样本在该函数上的取值。
（1）计算概率密度函数（PDF）的方法1 —— 使用 Numpy 模块
1 # 载入套件
2 import numpy as np
3
4
5 # 正态分布的概率密度函数(Probability Density Function, pdf)
6 def f(x, mean, std):
7 # 带入公式1,从而得到样本来自某个正态分布的概率
8 return (1/((2*np.pi*std**2) ** .5)) * np.exp(-0.5*((x-mean)/std)**2)
9
10
11 print(f(1, 0, 1))
代码运行结果：
（2）计算概率密度函数（PDF）的方法2 —— 使用 scipy.stats 模块
1 from scipy.stats import norm
2
3 # 平均数(mean)、标准差(std)
4 mean = 0
5 std = 1
6
7 # 计算来自正态分布N(0,1)的概率
8 print(norm.pdf(1, mean, std))
代码运行结果：
（3）绘制正态分布 N(0, 1) 的概率密度函数
1 import matplotlib.pyplot as plt
2 import numpy as np
3 from scipy.stats import norm
4
5 # 观察值范围
6 z1, z2 = -4, 4
7
8 # 平均数(mean)、标准差(std)
9 mean = 0
10 std = 1
11
12 # 样本点
13 x = np.arange(z1, z2, 0.001)
14 y = norm.pdf(x, mean, std)
15
16 # 绘图
17 plt.plot(x, y, 'black')
18
19 # 填色
20 plt.fill_between(x, y, 0, alpha=0.3, color='b')
21 # 连接（1， 0）和（1， f(1, 0, 1)）这两个点
22 plt.plot([1, 1], [0, norm.pdf(1, mean, std)], color='r')
23 plt.show()
代码运行结果：
范例2：如果有两个样本点 x=1、3，来自正态分布 N(1, 1) 及 N(2, 3) 的可能性哪一个比较大？
假设两个样本是独立的，故联合概率为两个样本概率相乘，使用 scipy.stats 模块计算概率。程序代码如下：
1 # 载入套件
2 from scipy.stats import norm
3
4 # 计算来自正态分布 N(1,1)的概率
5 mean = 1 # 平均数(mean)
6 std = 1 # 标准差(std)
7 # 根据公式2，可以计算出两个样本在正态分布函数中的发生概率
8 print(f'来自 N(1,1)的机率：{norm.pdf(1, mean, std) * norm.pdf(3, mean, std)}')
9
10 # 计算来自正态分布 N(2,3)的概率
11 mean = 2 # 平均数(mean)
12 std = 3 # 标准差(std)
13 # 根据公式2，可以计算出两个样本在正态分布函数中的发生概率
14 print(f'来自 N(2,3)的机率：{norm.pdf(1, mean, std) * norm.pdf(3, mean, std)}')
执行结果如下，表明来自 N(1, 1) 可能性比较大。
范例3：如果有一组样本，计算来自哪一个正态分布 N(μ, δ) 的概率最大，请依上面推理过程证明计算 μ、δ。
（1）对正态分布的概率密度函数（PDF）取对数（log）。
1 # 载入套件
2 from sympy import symbols, pi, exp, log
3
4 # 样本
5 data = [1, 3, 5, 3, 4, 2, 5, 6]
6
7 # x变数、平均数(m)、标准差(s)
8 x, m, s = symbols('x m s')
9
10 # 常态分配的机率密度函数(Probability Density Function, pdf)
11 pdf = (1/((2*pi*s**2) ** .5)) * exp(-0.5*((x-m)/s)**2)
12 # 显示 log(pdf) 函数
13 log_p = log(pdf)
14 print(log_p)
代码运行结果：
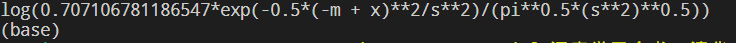
（2）带入样本数据 x（x是样本数据是确定的值，实际计算时要带入到函数中，这里未知数是 μ 和 δ）。
1 # 带入样本资数据
2 logP = 0
3 for xi in data:
4 # subs函数是用具体的数字替换掉变量的变量
5 logP += log_p.subs({x: xi})
6
7 print(logP)
代码运行结果：
（3）对上述函数使用 diff() 求其对平均数、标准差的偏微分（对应以上公式6-7）。
1 from sympy import diff
2
3 logp_diff_m = diff(logP, m) # 对平均数(m)偏微分
4 logp_diff_s = diff(logP, s) # 对变异数(s)偏微分
5
6 print('m 偏导数:', logp_diff_m)
7 print('s 偏导数:', logp_diff_s)
代码运行结果：
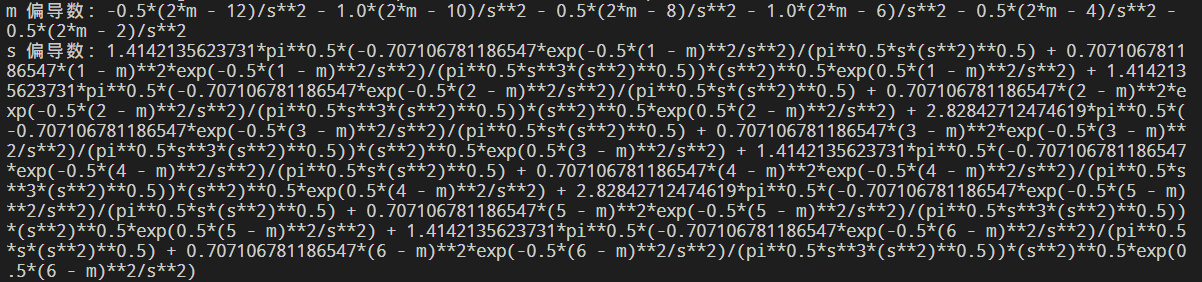
（4）使用 simplify() 简化偏导数。
1 from sympy import simplify
2
3 # 简化 m 偏导数
4 logp_diff_m = simplify(logp_diff_m)
5 print("simplify diff m")
6 print(logp_diff_m)
7 print()
8
9 # 简化 s 偏导数
10 logp_diff_s = simplify(logp_diff_s)
11 print("simplify diff s")
12 print(logp_diff_s)
代码运行结果：
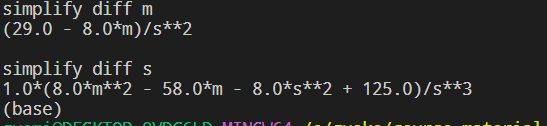
（5）联立方程式，令一阶导数为0，函数取得最大值，从而求得当函数取得最大值的时候对应的平均数 m 和 标准差 s。
1 from sympy import solve
2
3 funcs = [logp_diff_s, logp_diff_m]
4 # sympy.solve(表达式， 符号)
5 print(solve(funcs, [m, s]))
代码运行结果：
至此，通过以上证明过程求得的 μ 和 δ 分别为 3.625 和 1.57619002661481（标准差只能是正数）。
若不用以上证明过程，而是使用函数 numpy 模块自带的函数计算 μ 和 δ，那么，代码和结果如下：
1 import numpy as np
2 print("data = ", data)
3 print("mean = ", np.mean(data))
4 print("std = ", np.std(data))
代码运行结果：
由得到的 mean 值和 std 值可知，和最大似然估计法证明过程计算出来的平均数和标准差值一致。
