python 使用梯度下降法找最小值(Find the minimum using gradient descent)
最近在看《深度学习全书 公式+推导+代码+TensorFlow全程案例》—— 洪锦魁主编 清华大学出版社 ISBN 978-7-302-61030-4 这本书,在第2章 神经网络原理 中 2-3-3 偏微分的内容中有个使用梯度下降法找最小值的代码,在机器学习的很多问题中,都可以通过使用梯度下降算法最小化损失函数来解决,这个案例可以帮助大家更加深入理解梯度下降的原理,分享给大家~
假设f(x)=x2,接下来则使用梯度下降法找最小值。
逻辑思路:
(1)任意设定一起始点(x_start);
(2)计算该点的梯度 fd(x);
(3)沿着梯度更新 x,逐步逼近最佳解,幅度大小以学习率控制。新的 x = x - 学习率(Learning Rate) * 梯度;
(4)重复步骤(2)(3),判断梯度是否接近于0,若已很逼近于0,即可找到最佳解。
代码如下:
1 import numpy as np
2 import matplotlib.pyplot as plt
3 from numpy import arange
4 from matplotlib.font_manager import FontProperties
5 plt.ion()
6
7
8 # 函数 f(x)=x^2
9 def f(x): return x ** 2
10
11
12 # 一阶导数:dy/dx=2*x
13 def fd(x): return 2 * x
14
15
16 def GD(x_start, df, epochs, lr):
17 xs = np.zeros(epochs+1)
18 w = x_start
19 xs[0] = w
20 for i in range(epochs):
21 dx = df(w)
22 # 权重的更新
23 # W_NEW = W — 学习率(learning rate) x 梯度(gradient)
24 w += - lr * dx
25 xs[i+1] = w
26 return xs
27
28
29 # 超参数(Hyperparameters)
30 x_start = 5 # 起始权重
31 epochs = 25 # 执行周期数
32 lr = 0.1 # 学习率
33
34 # 梯度下降法, 函数 fd 直接当参数传递
35 w = GD(x_start, fd, epochs, lr=lr)
36 # 显示每一执行周期得到的权重
37 print(np.around(w, 4))
38
39 # 画图
40 color = 'r'
41 t = arange(-6.0, 6.0, 0.01)
42 plt.plot(t, f(t), c='b') # 用蓝色的线画出f(t)函数的图
43 plt.plot(w, f(w), c=color, label='lr={}'.format(lr)) # 用红色的线画出f(w)的图
44 plt.scatter(w, f(w), c=color, ) # 用红色的点画出f(w)上的点
45
46 # 设定中文字型
47 font = FontProperties(fname=r"c:\windows\fonts\msjhbd.ttc", size=20)
48 plt.title('梯度下降法', fontproperties=font) # 设置标题
49 plt.xlabel('w', fontsize=20) # 设置x坐标轴的标签
50 plt.ylabel('Loss', fontsize=20) # 设置y坐标轴的标签
51
52 # 矫正负号
53 plt.rcParams['axes.unicode_minus'] = False
54
55 plt.show()
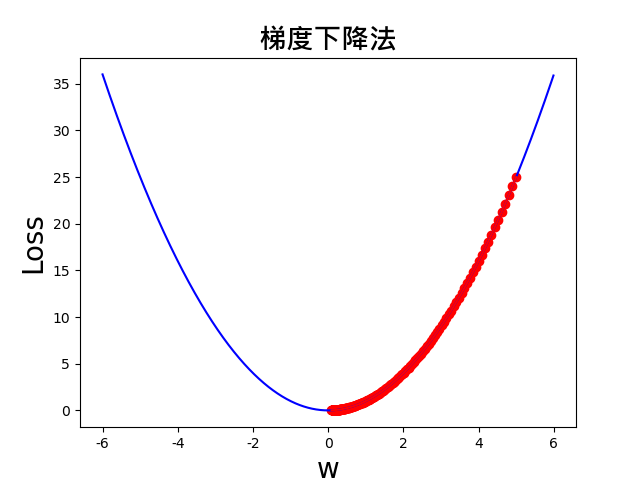
结果图如下,可以看出,从 w=5 开始,w 的值确实朝着梯度下降的方向,也就是最小值的方向走。
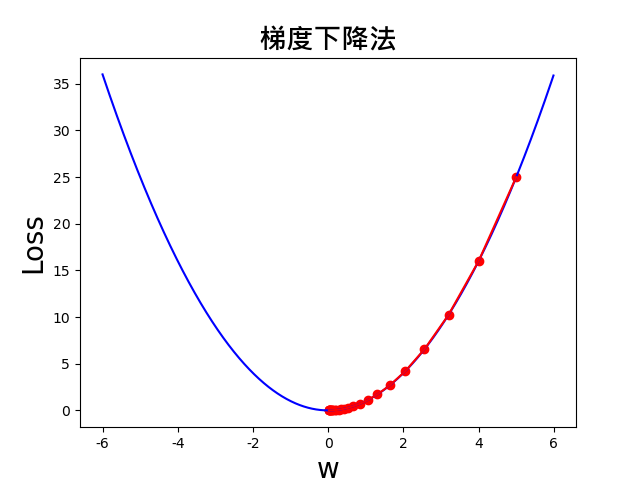
此外,我们可以改变 x_start, epochs, lr 三个变量的值,来观察下效果。
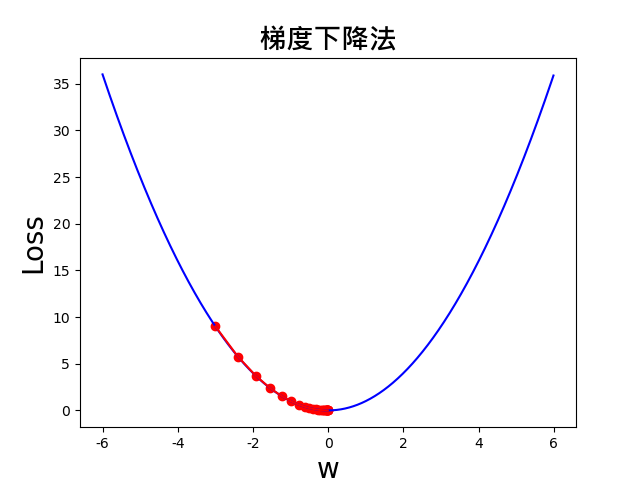
(1)当改变起始点的值,即 x_start = -3,可以观察到,依然可以找到最小值。
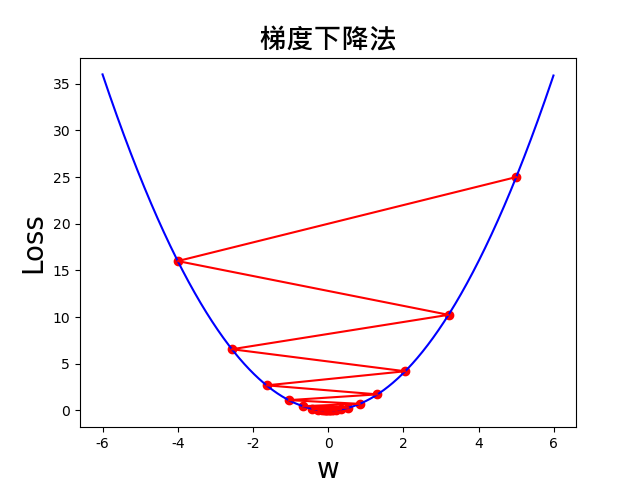
(2)设定学习率 lr=0.9,那么在函数复杂的情况下,可能存在跳过最小值的情况
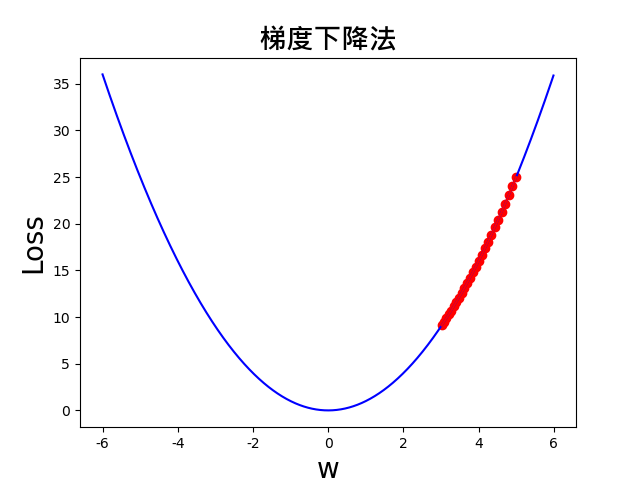
(3)设定学习率 lr=0.01,可以看到还未逼近最小值,就提早停止了。可就是我们经常说的训练不够。
(4)设定学习率 lr=0.01,再增加 epochs 的数值,这里设置 epochs=200,可以发现,效果会更接近最小值。
上述程序就是神经网络优化器求解的简化版。以一个简单的函数,帮助大家理解神经网络中梯度下降法的原理。


