2023.11.3 做题记录

CF349B *1700

$Igor$深深爱上了$Tanya$. 现在, $Igor$想表达他的爱意, 他便在$Tanya$家对面的墙上写下一串数字. $Igor$认为, 数字写得越大, $Tanya$越喜欢他. 不幸的是, 他只有$v$升油漆, 每个数字都会花掉一定的油漆$a_i$. $Igor$不喜欢$0$ 所以数中不会出现$0$. 问$Igor$能得到的最大的数是多少.

显然数的长度越大这个数越大，先用最少花费的数求出最大长度，然后从高位到低位挨着尝试替换即可。

#include<bits/stdc++.h>
#define lson rt << 1
#define rson rt << 1 | 1
using namespace std;
const int N = 2e5 + 10;
const int mod = 1e9 + 7;
 
inline int read() {
	int res = 0, f = 0; char ch = getchar();
	for(; !isdigit(ch); ch = getchar()) f |= (ch == '-');
	for(; isdigit(ch); ch = getchar()) res = (res << 1) + (res << 3) + (ch - '0');
	return f ? -res : res;
}
 
int V;
pair <int, int> a[15];
int ans[N << 3];
 
signed main() {
	V = read();
	for(int i = 1; i <= 9; i++) a[i].first = read(), a[i].second = i;
	int MinFy = INT_MAX, Minwz = 0;
	for(int i = 1; i <= 9; i++) {
		if(MinFy > a[i].first) MinFy = a[i].first, Minwz = a[i].second; 
		if(MinFy == a[i].first) Minwz = a[i].second;	
	}
	int Max_Len = V / MinFy;
	V -= Max_Len * MinFy;
	for(int i = 1; i <= Max_Len; i++) ans[i] = Minwz;
	for(int i = 1; i <= Max_Len; i++) {
		for(int j = 9; j > Minwz; j--) {
			if(V + MinFy >= a[j].first) {
				V += MinFy, V -= a[j].first, ans[i] = j;
				break;	
			} 
		}
	}
	if(!Max_Len) return puts("-1"), 0;
	for(int i = 1; i <= Max_Len; i++) cout << ans[i];
	return 0;
}
 

CF1450C1 Errich-Tac-Toe (Easy Version) *2100

屁也不会

直接进入题解。

题解已阅，狗屁不通。

比较显然的就是考虑一个 $3 \times 3$ 的矩阵。

比如下面这样啊：

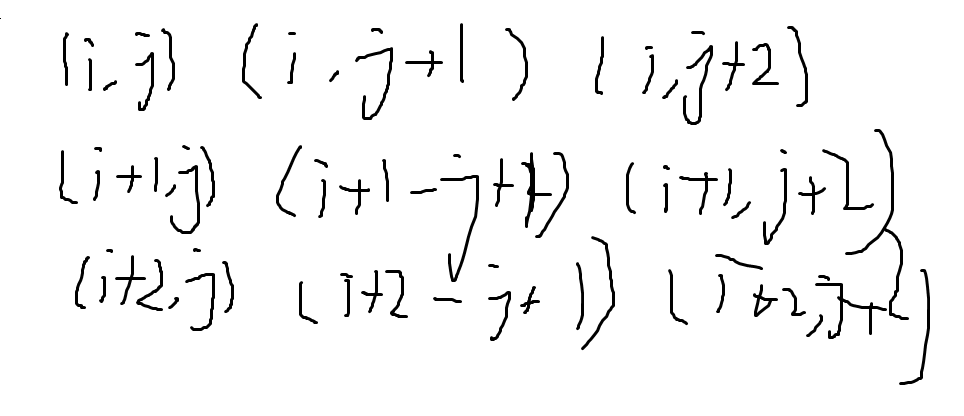
钦定 $(i,j)$ 为 $0$

发现得到这么个矩阵。

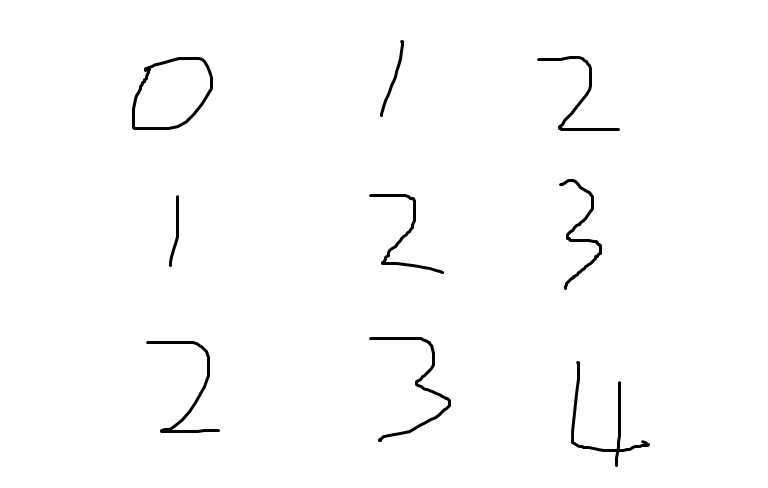
想了想要给他分为 $3$ 种颜色，按照 $(i+j) % 3$ 分配的话，在任意一个 $3 \times 3$ 的矩阵里，都可以通过涂一个最少颜色来平局，然后就统计即可。

#include<bits/stdc++.h>
#define lson rt << 1
#define rson rt << 1 | 1
using namespace std;
const int N = 2e5 + 10;
const int mod = 1e9 + 7;
 
inline int read() {
	int res = 0, f = 0; char ch = getchar();
	for(; !isdigit(ch); ch = getchar()) f |= (ch == '-');
	for(; isdigit(ch); ch = getchar()) res = (res << 1) + (res << 3) + (ch - '0');
	return f ? -res : res;
}
 
char ch[310][310];
int cnt[10];
 
void Main() {
	int n = read();
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= n; j++) ch[i][j] = getchar();
		getchar();
	}
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= n; j++) cnt[(i + j) % 3]++;
	}
	int Min = std::min(cnt[0], std::min(cnt[1], cnt[2]));
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= n; j++) {
			if((i + j) % 3 == Min && ch[i][j] == 'X') ch[i][j] = 'O';
		}
	}
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= n; j++) putchar(ch[i][j]);
		putchar('\n');
	}
	cnt[0] = cnt[1] = cnt[2] = 0;
}
signed main() {
	int T = read();
	while(T--) Main();
	return 0;
}
 

P5931 [清华集训2015] 灯泡 上位黄

随机跳到的 nb 题啊，之前就看他们做过，今天也来试试。

小数学题啊。

很显然的分类讨论吧。

当影子全在地上的时候，最大的情况就是影子刚好顶到墙上，由相似三角形可以知道。

设 $x$ 为到灯下端的距离。

$\frac{h}{H} = \frac{D - x}{D}$

$hD=(D-x)H$

$x = D \frac{H - h}{H}$

所以当 $x \le D \frac{H-h}{H}$ 时，影子全落在地面上。

设影子的长度为 $y$。

则 $\frac{h}{y}=\frac{H}{x+y}$

化简可得：$y = \frac{h}{H-h} x$

显然具有单调性，$x$ 最大的时候 $y$ 最大。

然后就是可以投射到墙上的时候。

设 $d$ 表示没墙多 🐍 的。

$\frac{h}{H} = \frac{D+d-x}{D+d}$

能得到 $d = \frac{H}{H-h} x + D$

$y = D - x + H \frac{Hx+DH-Dh}{Hx+2DH-2Dh}$

我急眼了，按推的公式写好像不对/cy

不做了，明天早上再补 /cy

CF1420B

考虑 $2^0 + 2^1 + ... + 2^n-1 = 2^n - 1$

所以考虑最高位是不是相同即可，当最高位想同的时候 $&$ 操作此位是 $1$，不同的时候 %^% 操作是 $1$。

显然答案为 $\sum C_{cnt_k}^{2}$，$cnt_k$ 表示最高位为第 $k$ 位的数的个数。