树论
树的直径
指树上最长的一条路径。
求法 \(1\) dfs
先随机一个点 dfs 一边, 求出最大深度的点,这个点一定是直径的一端,然后再 dfs 一遍,求出另一端,此时的距离就是树的直径。
分类讨论直径与dfs的关系就行了。
int n, dep[N], ans; vector <int> e[N];
void dfs(int u, int fa) {
dep[u] = dep[fa] + 1;
if(dep[u] > dep[ans]) ans = u;
for(int v : e[u]) if(v ^ fa) dfs(v, u);
}
signed main()
{
n = read();
for(int i = 1; i <= n - 1; i++) {
int u = read(), v = read();
e[u].push_back(v), e[v].push_back(u);
}
dfs(1, 0), dfs(ans, 0), print(dep[ans] - 1);
return 0;
}
求法 \(2\) dp
树形 dp,我们设 \(f[u][0 / 1]\) 分别表示 \(u\) 作为子树的根,到其叶子节点中的最大值和次大值。
显然答案是 \(\max(f[u][0] + f[u][1])\)。
int n, f[N][2], Maxdep;
vector <int> E[N];
void dfs(int u, int fa) {
f[u][0] = 0, f[u][1] = 0;
for(int v : E[u]) {
if(v == fa) continue;
dfs(v, u);
int tmp = f[v][0] + 1;
if(tmp > f[u][0]) f[u][1] = f[u][0], f[u][0] = tmp;
else if(tmp > f[u][1]) f[u][1] = tmp;
}
Maxdep = max(Maxdep, f[u][0] + f[u][1]);
}
signed main()
{
n = read();
for(int i = 1; i <= n - 1; i++) {
int u = read(), v = read();
E[u].push_back(v), E[v].push_back(u);
}
dfs(1, 0);
printf("%d\n", Maxdep);
return 0;
}
例题:P1099 [NOIP2007 提高组] 树网的核
发现数据范围很小,我们枚举路径的起点和终点,然后从路径上的点开始跑,找到距离最大的不是路径上点的点。
复杂度 \(\mathcal{O}(n^3)\)。
/**
* author: TLE_Automation
* creater: 2022.8.10
**/
#include<cmath>
#include<queue>
#include<cstdio>
#include<bitset>
#include<cstring>
#include<iostream>
#include<algorithm>
#define gc getchar
using namespace std;
typedef long long ll;
//#define int long long
const int N = 3e5 + 10;
const int MAXN = 2e5 + 10;
const int mod = 998244353;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
inline int gcd(int a, int b) {return !b ? a : gcd(b, a % b);}
inline void print(int x) {if (x < 0) putchar('-'), x = -x; if(x > 9) print(x / 10); putchar(x % 10 + '0');}
inline int ksm(int a, int b) {int base = a % mod, res = 1; while(b){if(b & 1) res = (res * base) % mod; base = (base * base) % mod, b >>= 1;}return res % mod;}
inline int mul(int a, int b) {int base = a % mod, res = 0; while(b){if(b & 1) res = (res + base) % mod; base = (base + base) % mod, b >>= 1;}return res % mod;}
inline char readchar() {static char buf[100000], *p1 = buf, *p2 = buf; return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;}
inline int read() { int res = 0, f = 0; char ch = gc();for (; !isdigit(ch); ch = gc()) f |= (ch == '-'); for (; isdigit(ch); ch = gc()) res = (res << 1) + (res << 3) + (ch ^ '0'); return f ? -res : res;}
const int M = 305;
struct Node {int u, v, w, nxt; } e[M << 1];
int n, s, num_adge = 0, head[N], dis[N], dep[N], f[N], top[N], siz[N], son[N];
void add_adge(int u, int v, int w) {e[++num_adge] = (Node) {u, v, w, head[u]}, head[u] = num_adge; }
void dfs(int u, int fa) {
dep[u] = dep[fa] + 1, f[u] = fa;
for(int i = head[u]; i; i = e[i].nxt) {
int v = e[i].v;
if(v == fa) continue;
dis[v] = dis[u] + e[i].w;
dfs(v, u);
}
}
bool vis[M], inque[M];
int ans = INF, Maxdep = 0;
void dfs1(int u, int sum) {
if(vis[u]) return;
vis[u] = 1;
Maxdep = max(Maxdep, sum);
for(int i = head[u]; i; i = e[i].nxt) {
int v = e[i].v;
if(vis[v]) continue;
dfs1(v, sum + e[i].w);
}
}
signed main()
{
n = read(), s = read();
for(int i = 1; i <= n - 1; i++) {
int u = read(), v = read(), w = read();
add_adge(u, v, w), add_adge(v, u, w);
}
dfs(1, 0);
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
int x = i, y = j;
for(int k = 1; k <= n; k++) vis[k] = 0, inque[k] = 0;
vis[x] = 1, inque[x] = 1, vis[y] = 1, inque[y] = 1;
int sum = 0;
while(x ^ y) {
if(dis[x] < dis[y]) swap(x, y);
sum += dis[x] - dis[f[x]], x = f[x];
vis[x] = 1, vis[y] = 1, inque[x] = 1, inque[y] = 1;
}
if(sum > s) continue;
Maxdep = 0;
for(int k = 1; k <= n; k++) {
if(!inque[k]) continue;
vis[k] = 0;
dfs1(k, 0);
}
ans = min(ans, Maxdep);
}
}
printf("%d\n", ans);
return 0;
}
树的重心
在一棵树中,如果我们选择某个结点为根,可以使得它的所有子树中最大的子树最小,那么这个结点就被称作这棵树的重心。
性质:
-
以重心为树根时,所有子树的大小不超过全树大小的一半。
-
如果树的所有边权都为1,那么树中所有点到某个点的距离和中,到重心的距离和是最小的;如果有两个重心,那么到它们的距离和一样。反过来,距离和最小的点一定是重心。
-
把两棵树通过一条边相连得到一棵新的树,则新的重心在较大的一棵树一侧的连接点与原重心之间的简单路径上。如果两棵树大小一样,则重心就是两个连接点。
另外一种说法:把两棵树通过一条边相连得到一棵新的树,那么新的树的重心在连接原来两棵树的重心的路径上。 -
在一棵树上添加或删除一个叶子,那么它的重心最多只移动一条边的距离。
-
一颗树最多只有两个重心,且这两个重心一定是相邻的。此时树一定有偶数个节点,且可以被划分为两个大小相等的分支,每个分支各自包含一个重心。
-
一棵树的重心一定在根节点所在的重链上。
-
一棵树的重心一定是以该树根节点重儿子为根的子树的重心的祖先。
-
往树上增加或减少一个叶子,如果原节点数是奇数,那么重心可能增加一个,原重心仍是重心;如果原节点数是偶数,重心可能减少一个,另一个重心仍是重心。
求法:
\(f[u]\) 表示 \(u\) 的最大子树大小。
树形 dp 搞一搞。
void dfs(int u, int fa) {
siz[u] = 1;
for(int v : E[u]) {
if(v == fa) continue;
dfs(v, u), siz[u] += siz[v];
f[u] = max(f[u], siz[v]);
}
f[u] = max(f[u], n - siz[u]);
if(!ans || f[u] < f[ans]) ans = u;
}
最近公共祖先 LCA
求法:倍增 和 树剖。
倍增求法:
我们设 \(f_{u, i}\) 表示 \(u\) 的第 \(2^i\) 祖先。
我们记录 \(dep\),在第一个 dfs 中处理出来。
然后求 \(x\) 和 \(y\) 的 LCA 时,先把 \(x\) 和 \(y\) 跳到同一高度。
然后俩个点一起跳,然后不断的跳,为了防止跳过去,就是不相等就跳,最后答案就是 \(x\) 和 \(y\) 的爹。
void dfs(int u, int fa) {
dep[u] = dep[fa] + 1, f[u][0] = fa;
for(int i = 1; i <= 22; i++)
f[u][i] = f[f[u][i - 1]][i - 1];
for(int i = head[u]; i; i = e[i].nxt) {
int v = e[i].v;
if(v == fa) continue;
dfs(v, u);
}
}
int LCA(int x, int y) {
if(dep[x] < dep[y]) swap(x, y);
for(int i = 22; i >= 0; i--) {
if(dep[f[x][i]] >= dep[y]) x = f[x][i];
if(x == y) return x;
}
for(int i = 22; i >= 0; i--) {
if(f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
}
return f[x][0];
}
树剖:
void dfs1(int u, int Fa) {
dep[u] = dep[Fa] + 1, siz[u] = 1, fa[u] = Fa;
for(int v : E[u]) {
if(v == Fa) continue;
dfs1(v, u); siz[u] += siz[v];
if(siz[son[u]] < siz[v]) son[u] = v;
}
}
void dfs2(int u, int tp) {
top[u] = tp;
if(son[u]) dfs2(son[u], tp);
for(int v : E[u]) {
if(v == son[u] || v == fa[u]) continue;
dfs2(v, v);
}
}
int LCA(int x, int y) {
while(top[x] ^ top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y);
x = fa[top[x]];
}
return dep[x] < dep[y] ? x : y;
}
虚树
用来优化树形 dp 的,是个假的树,所以叫虚树。
虚树可以理解为把一些用不到的,没必要的状态给删去了。
那什么是有用的呢,就是有用的节点和他们的 LCA。
构造方法:
我们不可能暴力去加入,这样是 \(\mathcal{O}(k^2)\) 的。
我们用一个栈来维护最右链,表面这条链左边的虚树已经建立完成。
我们先按 dfs 序来排序,然后把根节点加入栈中。
假如当前要加入的节点为 \(now\),栈顶元素 \(stack[top]\)。
如果 \(LCA(now, stack[top])\) \(= stack[top]\) 说明现在这个 \(now\) 还在当前链上,直接加入栈中。

如果 \(LCA(now, stack[top])\) 不等于 \(stack[top]\),说明当前的链已经建立完成,我们维护的是最右链,把 \(LCA\) 之前的元素一一弹出,如果 \(LCA\) 未加入也要加入进去。
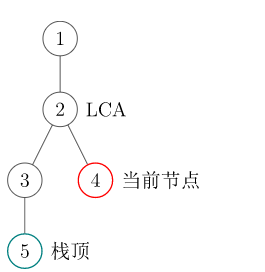
不断的这样操作,虚树就建立完成了。


 树论
树论

 浙公网安备 33010602011771号
浙公网安备 33010602011771号