浅析快速傅里叶变换
简介
快速傅里叶变换(Fast Fourier Transform)是一种可以在 $O(n\log n) $ 复杂度下完成离散傅里叶变换(Discrete Fourier Transfrom)的算法,常应用于加速多项式乘法。
多项式表示法
系数表示法
系数表示法就是用多项式各项系数来表达这个多项式:
点值表示法
点值表示法就是把多项式看作一个函数,对于一个 \(n\) 次多项式,任取 \(n+1\) 个在函数上的点,这样可以唯一确定这个多项式:
复数
在推导傅里叶变换前,我们需要掌握一些复数的基本性质:
- 复数运算满足结合律/交换律/分配律
- 复数 \(z=a+bi\) 的模长 \(|z|=\sqrt{a^2+b^2}\) ,幅角 \(\theta\) 为实轴的正半轴逆时针旋转到 \(z\) 的有向角度
- 两个复数的乘法满足模长相乘,幅角相加
单位根
定义
将复平面上的单位圆等分成 \(n\) 个部分,定义其中幅角为正且最小的等分点对应的复数为 \(n\) 次单位根,记作 \(\omega_n\) ,那么其余的 \(n-1\) 个等分点对应的复数分别为 \(\omega_n^2,\omega_n^3,\cdots,\omega_n^n\) ,其中 \(\omega_n^n=\omega_n^0=1\) ,一般地,有:
当 \(n=4\) 时图像如下:
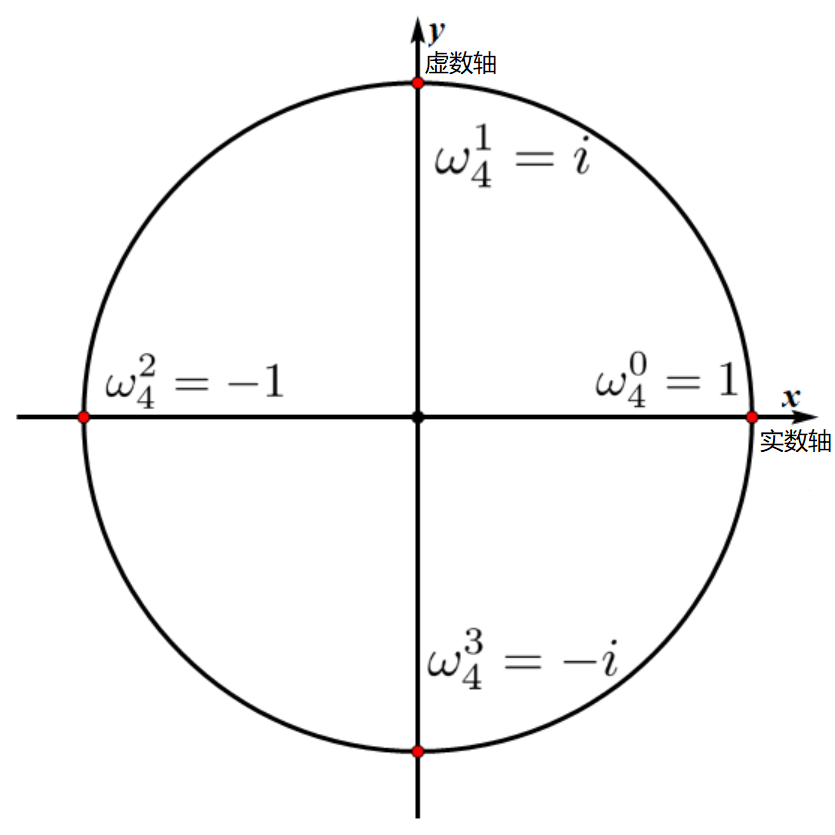
折半定理
由几何意义/代入公式即可证明
消去定理
由几何意义/代入公式即可证明
离散傅里叶变换
考虑一个含 \(n\) 项( \(n=2^t,t\in\mathbb{N}\) )的多项式 \(A(x)\) ,已知它的系数表示,将 \(n\) 次单位根的 \(0\sim n-1\) 次幂分别代入 \(A(x)\) 得到它的点值表示,这一过程称为离散傅里叶变换(Discrete Fourier Transform)
如果朴素地代入求值,复杂度显然为 \(O(n^2)\) ,FFT利用了单位根的一些性质来降低复杂度,对于 \(A(x)=a_0+a_1x+\cdots+a_{n-1}x^{n-1}\) ,我们按照奇偶进行分组:
设
可以得到:
分类讨论,当 \(0\leq k\leq \frac n 2-1\) 时
当 \(\frac n 2\leq k+\frac n 2\leq n-1\) 时
所以,如果求出了 \(A_1(x),A_2(x)\) 分别在 \(\omega_{\frac n 2}^0,\omega_{\frac n 2}^1,\cdots,\omega_{\frac n 2}^{\frac n 2-1}\) 的值,就可以用 \(O(n)\) 求出 \(A(\omega_n^0),A(\omega_n^1),\cdots,A(\omega_n^{n-1})\) ,那么就得到了 \(A(x)\) 的点值表示
FFT的时间复杂度 \(T(n)\) 满足:
逆离散傅里叶变换
已知一个项数为 \(2\) 的次幂的多项式的点值表示,求它的系数表示,这一过程叫做逆离散傅里叶变换(Inverse Discrete Fourier Transform) ,我们仍可以在稍加变形后用FFT解决这一问题
设 \(\{d_0,d_1,\cdots,d_{n-1}\}\) 为多项式 \(\{a_0,a_1,\cdots,a_{n-1}\}\) 经过FFT得到的结果,即 \(d_i=A(\omega_n^i)\) ,构造一个多项式:
设 \(c_k=F(\omega_n^{-k})=\sum_{i=0}^{n-1}d_i\cdot(\omega_n^{-k})^i\)
那么有:
设 \(S(j,k)=\sum_{i=0}^{n-1}(\omega_n^i)^{j-k}\)
若 \(j=k\) ,\(S(j,k)=n\)
若 \(j\not= k\) ,根据等比求和公式有:
所以 \(\forall j,k,S(j,k)=[j=k]\cdot n\)
代入原式得:
FFT模板
递归
typedef complex<double> cp;
const int MAX_N = 1 << 20;
//if FFT, inv = false
bool inv = false;
//return w(n, k) or w(n, -k)
cp omega(int n, int k)
{
if(inv)
return cp(cos(2 * M_PI / n * k), sin(2 * M_PI / n * k));
return cp(cos(2 * M_PI / n * k), -sin(2 * M_PI / n * k));
}
void fft(cp *a, int n)
{
if(n == 1)
return;
static cp buf[MAX_N];
int mid = n >> 1;
for(int i = 0; i < mid; i++) {
buf[i] = a[i << 1];
buf[i + mid] = a[i << 1 | 1];
}
memcpy(a, buf, sizeof(cp) * (n + 1));
cp *a1 = a, *a2 = a + mid;
fft(a1, mid);
fft(a2, mid);
for(int i = 0; i < mid; i++) {
cp t = omega(n, i);
buf[i] = a1[i] + t * a2[i];
buf[i + mid] = a1[i] - t * a2[i];
}
memcpy(a, buf, sizeof(cp) * (n + 1));
}
优化
递归版本的FFT需要辅助数组,并且递归产生了较大的常数,所以我们把每次分组的情况列举出来尝试优化
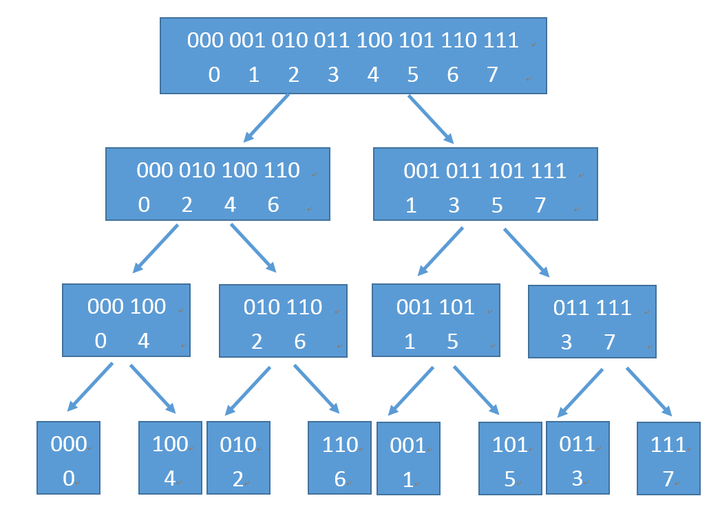
观察到每一个位置的数其实都是原来位置上的数的二进制位翻转了一下
于是我们可以先把原数组调整成最底层的位置,然后从倒数第二层逐层向上计算,这就是FFT的 Cooley-Tukey 算法,在这一算法中,合并操作被称为蝴蝶操作
从 \(1\) 开始由上到下对每一层编号,则从第 \(i\) 层到第 \(i-1\) 层需要 \(2^{i-1}\) 次合并。假设 \(A_1(\omega_{\frac n 2}^k)\) 和 \(A_2(\omega_{\frac n 2}^k)\) 分别存在 \(a[k]\) 和 \(a[k+\frac n 2]\) 中, \(A(\omega_n^k)\) 和 \(A(\omega_n^{k+\frac n 2})\) 将要被存放在 \(buf[k]\) 和 \(buf[k+\frac n 2]\) 中,合并的单位操作可表示为:
加入一个临时变量并改变合并顺序,我们就可以在原数组内合并
typedef complex<double> cp;
const int MAX_N = 1 << 22;
const double PI = acos(-1.0);
cp omega[MAX_N], inv[MAX_N];
cp x1[MAX_N], x2[MAX_N];
int sum[MAX_N << 1];
void init(int n)
{
for(int i = 0; i < n; i++) {
double a = cos(2 * PI / n * i), b = sin(2 * PI / n * i);
omega[i] = cp(a, b);
inv[i] = cp(a, -b);
}
}
void transform(cp *a, int n, const cp *omega)
{
for(int i = 0, j = 0; i < n; i++) {
if(i > j)
swap(a[i], a[j]);
for(int l = n >> 1; (j ^= l) < l; l >>= 1)
continue;
}
for(int i = 2; i <= n; i <<= 1) {
int mid = i >> 1;
for(cp *p = a; p != a + n; p += i) {
for(int j = 0; j < mid; j++) {
cp t = omega[n / i * j] * p[mid + j];
p[mid + j] = p[j] - t;
p[j] = p[j] + t;
}
}
}
}
void dft(cp *a, int n)
{
transform(a, n, omega);
}
void idft(cp *a, int n)
{
transform(a, n, inv);
for(int i = 0; i < n; i++)
a[i] /= n;
}
多项式乘法
原理
考虑已知两个多项式的系数表示 \(A(x)=\{a_0,a_1,\cdots,a_n\},B(x)=\{b_0,b_1,\cdots b_m\}\) ,要求它们的乘积的系数表示 \(C(x)=\{c_0,c_1,\cdots,c_{m+n}\}\) ,可以得到:
这样做的复杂度为 \(O(n\times m)\) ,可以用这段代码表示:
for(int i = 0; i < n; i++)
for(int j = 0; j < m; j++)
c[i + j] += a[i] * b[j];
考虑如何用点值表示简化计算,对于任意 \(n,m\) ,可以找到一个 \(t\) 满足 \(2^t\geq2\max(n,m)\) 且 \(2^{t-1}<2\max(n,m)\) ,我们把 \(A(x),B(x)\) 写成 \(t\) 次多项式的形式,即:
再用DFT得到 \(A(x),B(x)\) 的点值表示,可以用 \(O(t)\) 推出 \(C(x)\) 的点值表示:
再用IDFT将 \(C(x)\) 的点值表示转化为系数表示即可
例题
高精度乘法运算可以看作多项式的乘法运算,求出多项式乘法结果后代入 \(x=10\) 即可
#include<bits/stdc++.h>
using namespace std;
typedef complex<double> cp;
const int MAX_N = 1 << 22;
const double PI = acos(-1.0);
cp omega[MAX_N], inv[MAX_N];
cp x1[MAX_N], x2[MAX_N];
int sum[MAX_N << 1];
void init(int n)
{
for(int i = 0; i < n; i++) {
double a = cos(2 * PI / n * i), b = sin(2 * PI / n * i);
omega[i] = cp(a, b);
inv[i] = cp(a, -b);
}
}
void transform(cp *a, int n, const cp *omega)
{
for(int i = 0, j = 0; i < n; i++) {
if(i > j)
swap(a[i], a[j]);
for(int l = n >> 1; (j ^= l) < l; l >>= 1)
continue;
}
for(int i = 2; i <= n; i <<= 1) {
int mid = i >> 1;
for(cp *p = a; p != a + n; p += i) {
for(int j = 0; j < mid; j++) {
cp t = omega[n / i * j] * p[mid + j];
p[mid + j] = p[j] - t;
p[j] = p[j] + t;
}
}
}
}
void dft(cp *a, int n)
{
transform(a, n, omega);
}
void idft(cp *a, int n)
{
transform(a, n, inv);
for(int i = 0; i < n; i++)
a[i] /= n;
}
int main()
{
string s1, s2;
cin >> s1 >> s2;
int len = 1, len1 = s1.size(), len2 = s2.size();
while(len < len1 * 2 || len < len2 * 2)
len <<= 1;
for(int i = 0; i < len1; i++)
x1[i] = cp(s1[len1 - i - 1] - '0');
for(int i = len1; i < len; i++)
x1[i] = cp(0);
for(int i = 0; i < len2; i++)
x2[i] = cp(s2[len2 - i - 1] - '0');
for(int i = len2; i < len; i++)
x2[i] = cp(0);
init(len);
dft(x1, len);
dft(x2, len);
for(int i = 0; i < len; i++)
x1[i] = x1[i] * x2[i];
idft(x1, len);
for(int i = 0; i < len; i++)
sum[i] = int(x1[i].real() + 0.5);
for(int i = 0; i < len; i++) {
sum[i + 1] += sum[i] / 10;
sum[i] %= 10;
}
len = len1 + len2 - 1;
while(sum[len] == 0 && len > 0)
len--;
for(int i = len; i >= 0; i--)
putchar(sum[i] + '0');
putchar('\n');
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号