Luogu P1350 车的放置

题目

Luogu P1350

有下面这样一个网格棋盘， \(a,b,c,d\) 表示了对应边的长度，也就是对应格子数：

当 \(a=b=c=d=2\) 时对应下面这个棋盘：

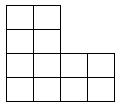
要在这个棋盘上放置 \(k\) 个互不攻击的车，也就是 \(k\) 个车没有两个再同一行或同一列，求方案数

分析

设上方 \(a\times b\) 的矩形中放了 \(i\) 个车，则下方 \(d\times(a+c)\) 的矩形中放了 \(k-i\) 个车，设 \(f(x,y,z)\) 为在 \(x\times y\) 的矩形中放 \(z\) 个车的方案数，则答案为：

\[\sum_{i=0}^k f(a,b,i)f(a+c,d,k-i) \]

考虑 \(f\) 的表达式，在 \(x\) 行中选 \(z\) 行作为放车的行，在 \(y\) 列中选 \(z\) 列作为放车的列，对于已经确定行的车，它们所在的列可以任意交换：

\[f(x,y,z)=\binom{x}{z}\binom{y}{z}z! \]

代码

#include<bits/stdc++.h>
using namespace std;

const int MOD = 100003;
long long fact[2000 + 5];

int qpow(int a, int b)
{
    if(b == 0)
        return 1;
    int res = qpow(a, b / 2);
    if(b % 2)
        return 1ll * res * res % MOD * a % MOD;
    return 1ll * res * res % MOD;
}

int C(int n, int m)
{
    if(m > n || m < 0 || n < 0)
        return 0;
    return fact[n] * qpow(fact[m] * fact[n - m] % MOD, MOD - 2) % MOD;
}

int main()
{
    fact[0] = 1;
    for(int i = 1; i <= 2000; i++)
        fact[i] = fact[i - 1] * i % MOD;
    int a, b, c, d, k;
    cin >> a >> b >> c >>d >> k;
    int t = min(b, k);
    int ans = 0;
    for(int i = 0; i <= t; i++) {
        int res = 1ll * C(b, i) * C(a, i) % MOD * fact[i] % MOD * C(d, k - i) % MOD * C(a + c - i, k - i) % MOD * fact[k - i] % MOD;
        ans = (ans +  res) % MOD;
    }
    cout << ans << endl;
    return 0;
}