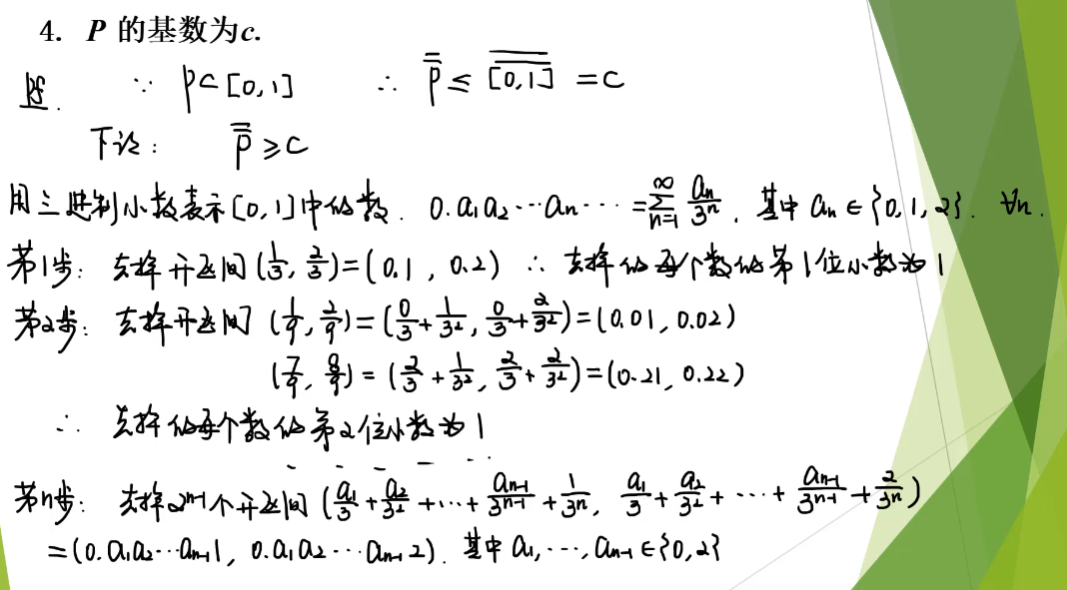康托尔三分集的基数是C，证明

 

1，用3进制来表示【0,1】那么康托尔集去掉的部分是包含1的小数（比如0.1，0.21，0.221）是包含在康托尔集P中的，但是这些数是可数个，我们就当它去掉了，只要证明剩下的数的集合基数任然是C就可以了）

2，那么剩下的小数是只由0,2组成的，用【0,1】区间去映射剩下的小数，（把【0,1】区间的小数转换成2进制，把剩下的小数也转换成二进制）这个映射是单射，而且是满射，

3，康托尔集的数字仍然是无穷多个，无穷位数，而且去掉的集合的基数显然也是c，这很神奇，可见c不是一个确定的数，也不是无穷