海涅博雷尔定理(草根证明,自用)
证明海涅博雷尔定理:
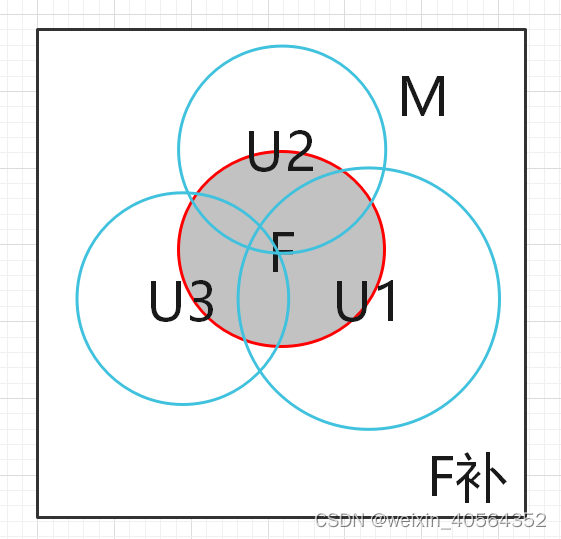
1,引理:紧集的闭子集是紧集
设,M是紧集,F是被U1,U2,U3......开集列覆盖的闭集,F属于M.
那么U1,U2,U3.....的并集再并上F的补集,就能够覆盖M(F的补集是开集).
因为M是紧集,所以在U1,U2,U3,......并上F的补集的M的无限覆盖开集中,可以找到有限个开集覆盖M(这些集合中可以包含F的补,也可以不包含),所以也能够找到有限个开集覆盖F。
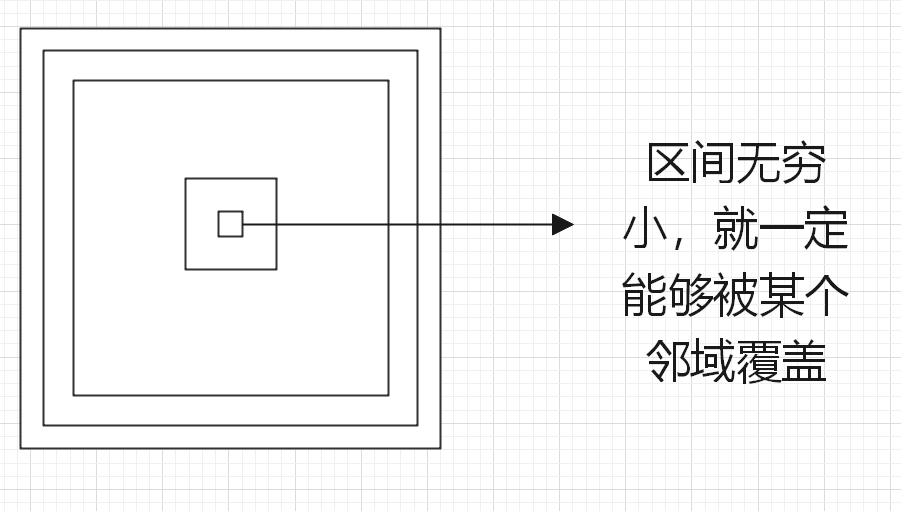
2,引理2:有限闭区间是紧集.
如果有限闭区间,没有有限个开区间覆盖,那么至少有一个子区间存在 无穷多个开区间覆盖,这个子区间可以证明是无穷小的,而无穷小的空间是能够被别的开区间覆盖的,所以,这是矛盾的

3,定理:在Rn空间中的紧集是有界闭集
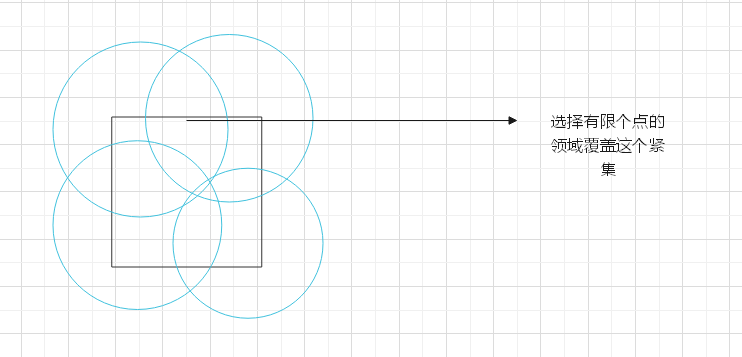
选择有限个点的有限领域,覆盖这个紧集,则证明有限个开领域的并集是有界集
证明:紧集在欧式空间是闭集
因为在m的补集外面总能找到,任意的点的领域是属于m的补集,证明m的补集是开集,(开区间和开区间,之间永远无法接触)