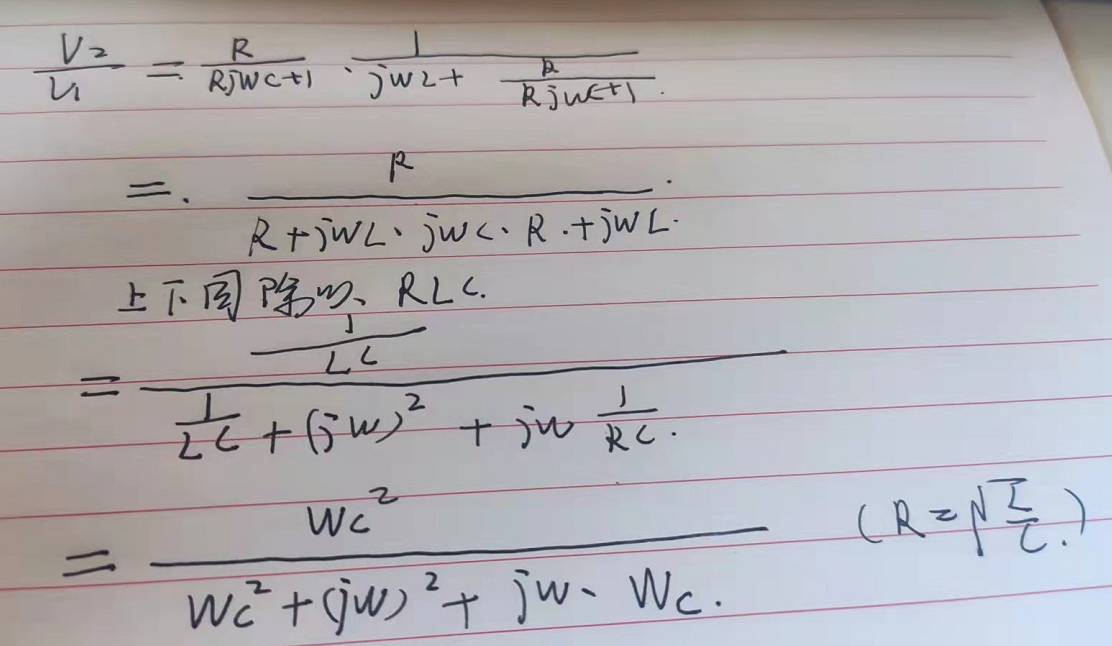信号与系统-4 傅里叶变换

信号的正交与分解，

 

 

 

 

 a0 用1/2，是吧系数归入到同用公式里

dirichlet条件，间断点两侧有极限，有左右的倒数

 

 

 

 

 

 

 

 

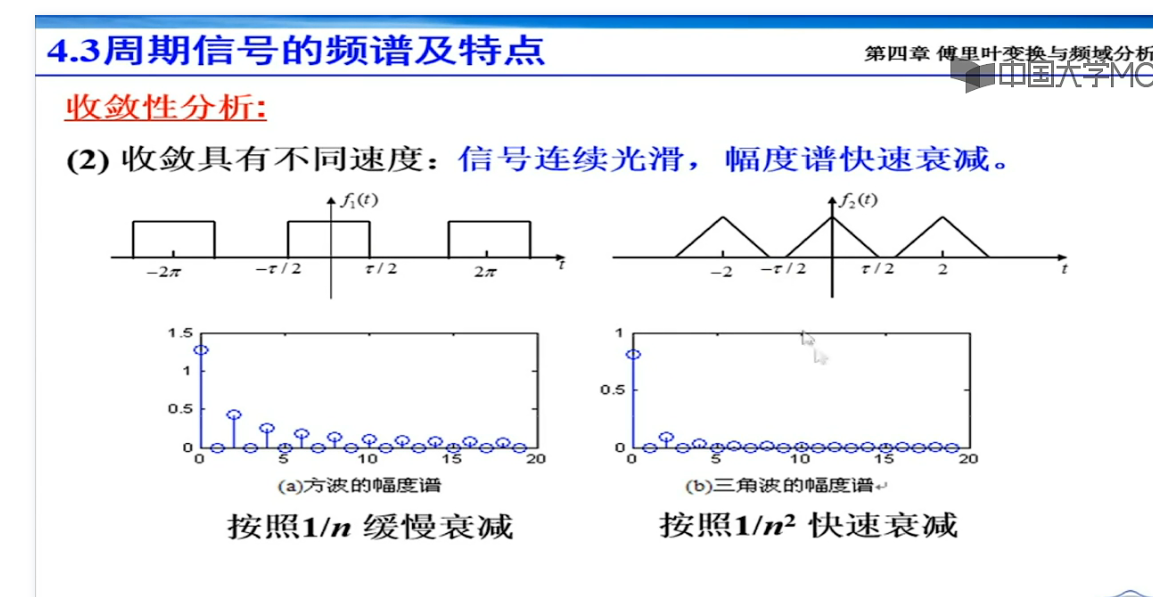
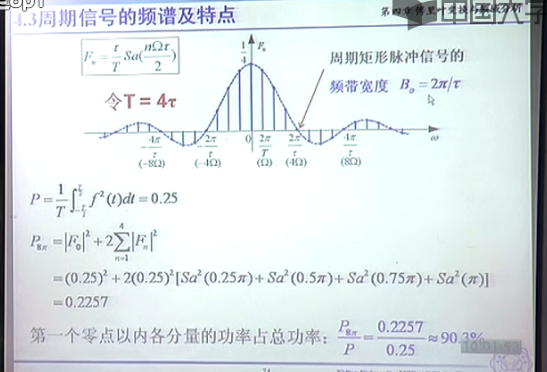
方波的傅里叶变换

 

 

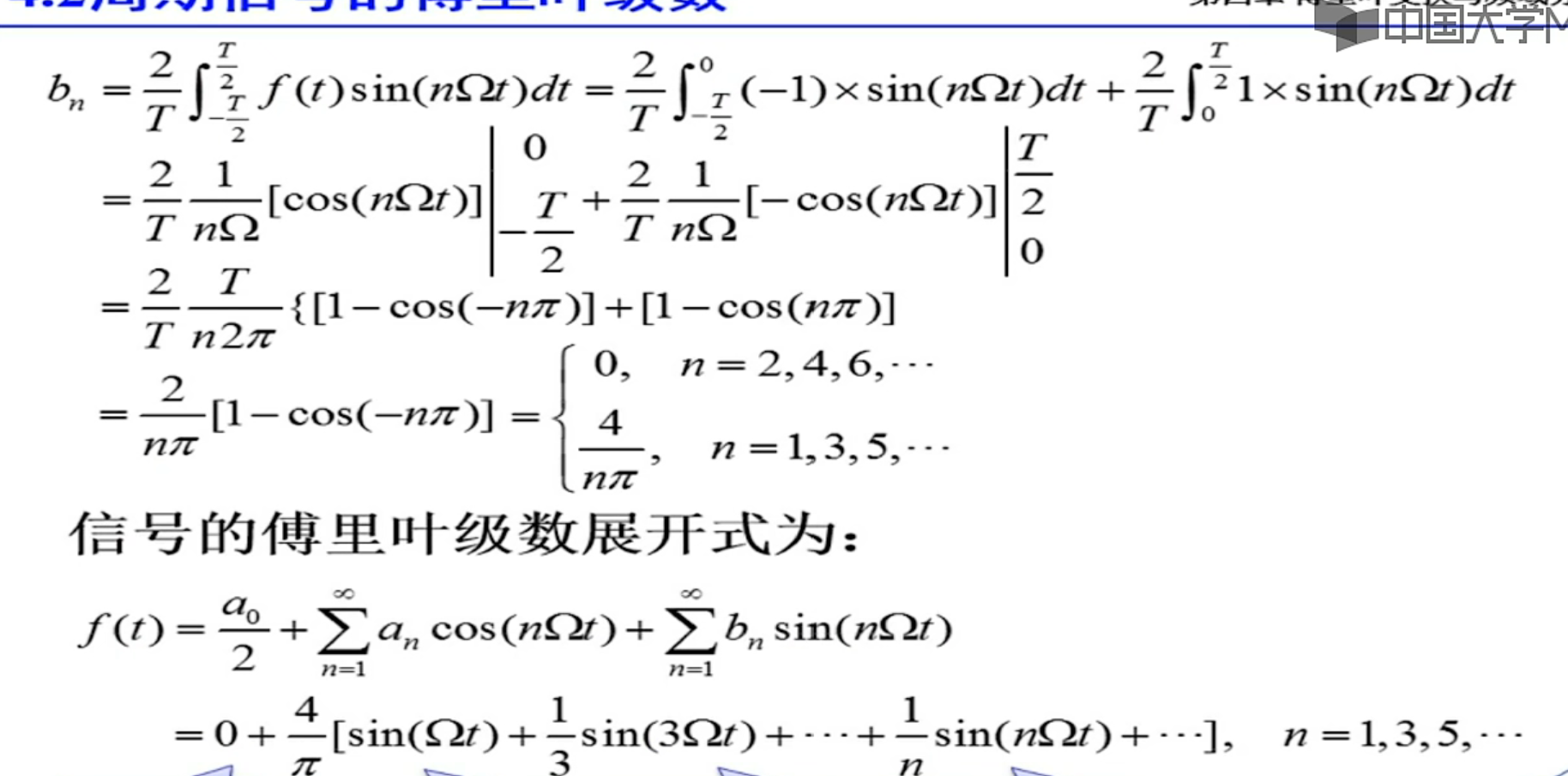
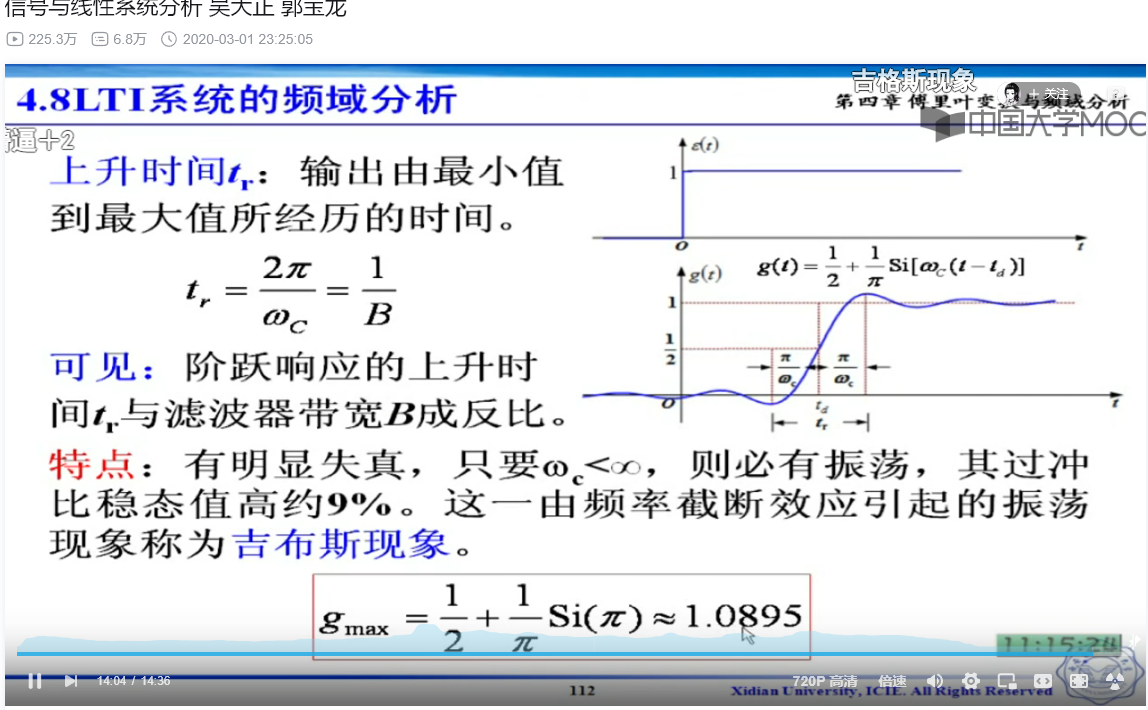
 吉布斯现象

 

 

 

 

 

 

 

 

 

 

 

 

 

 

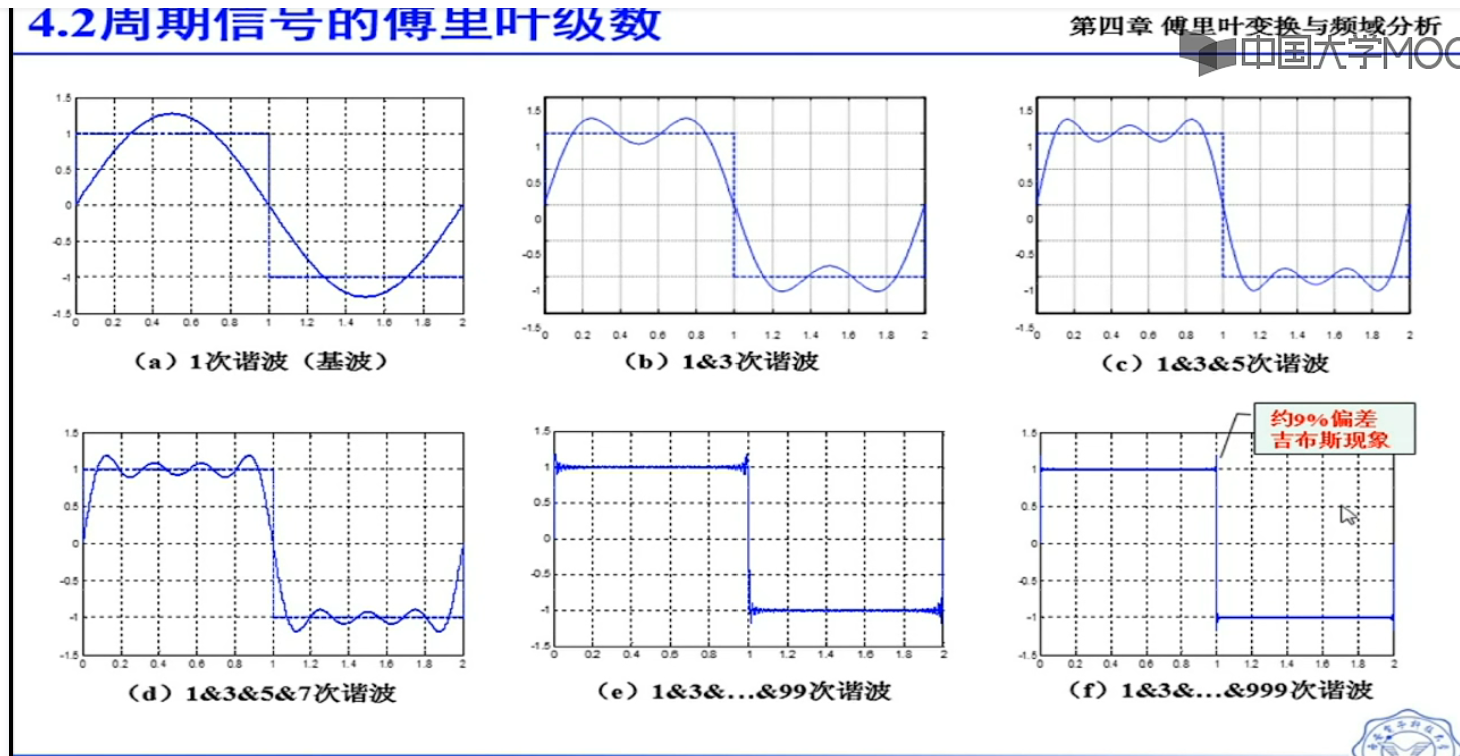
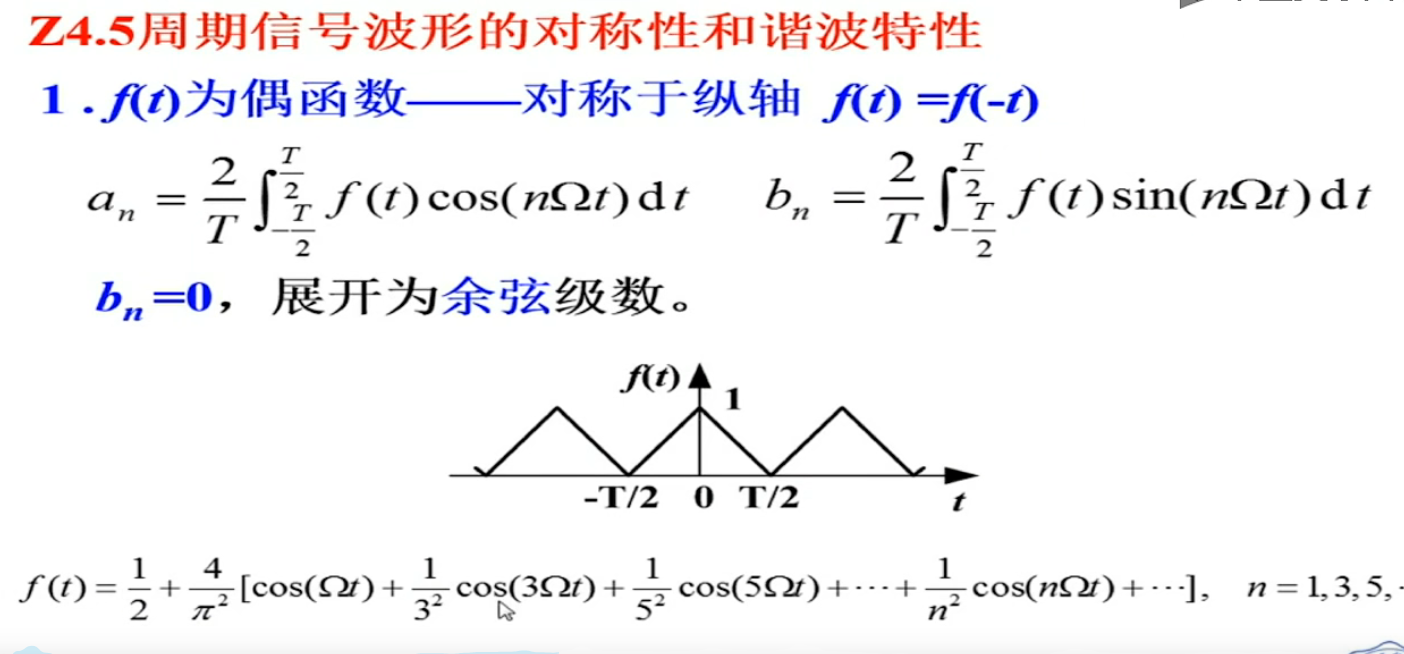
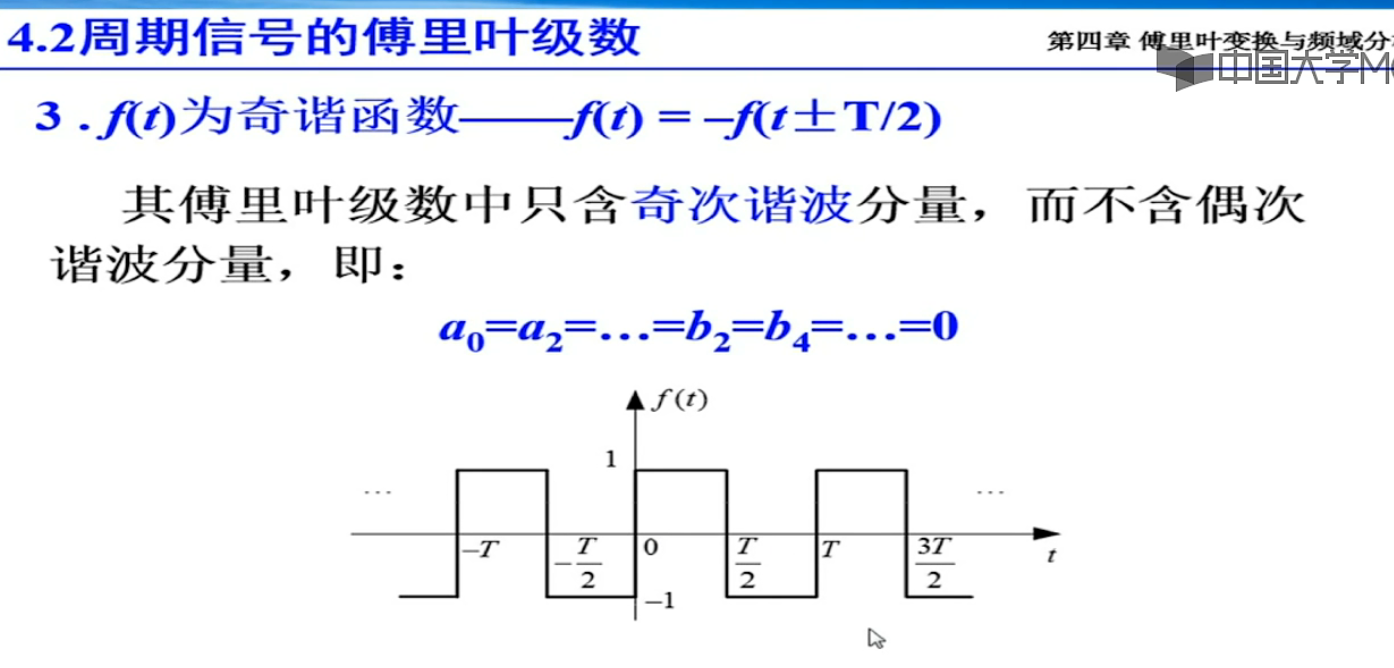
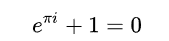
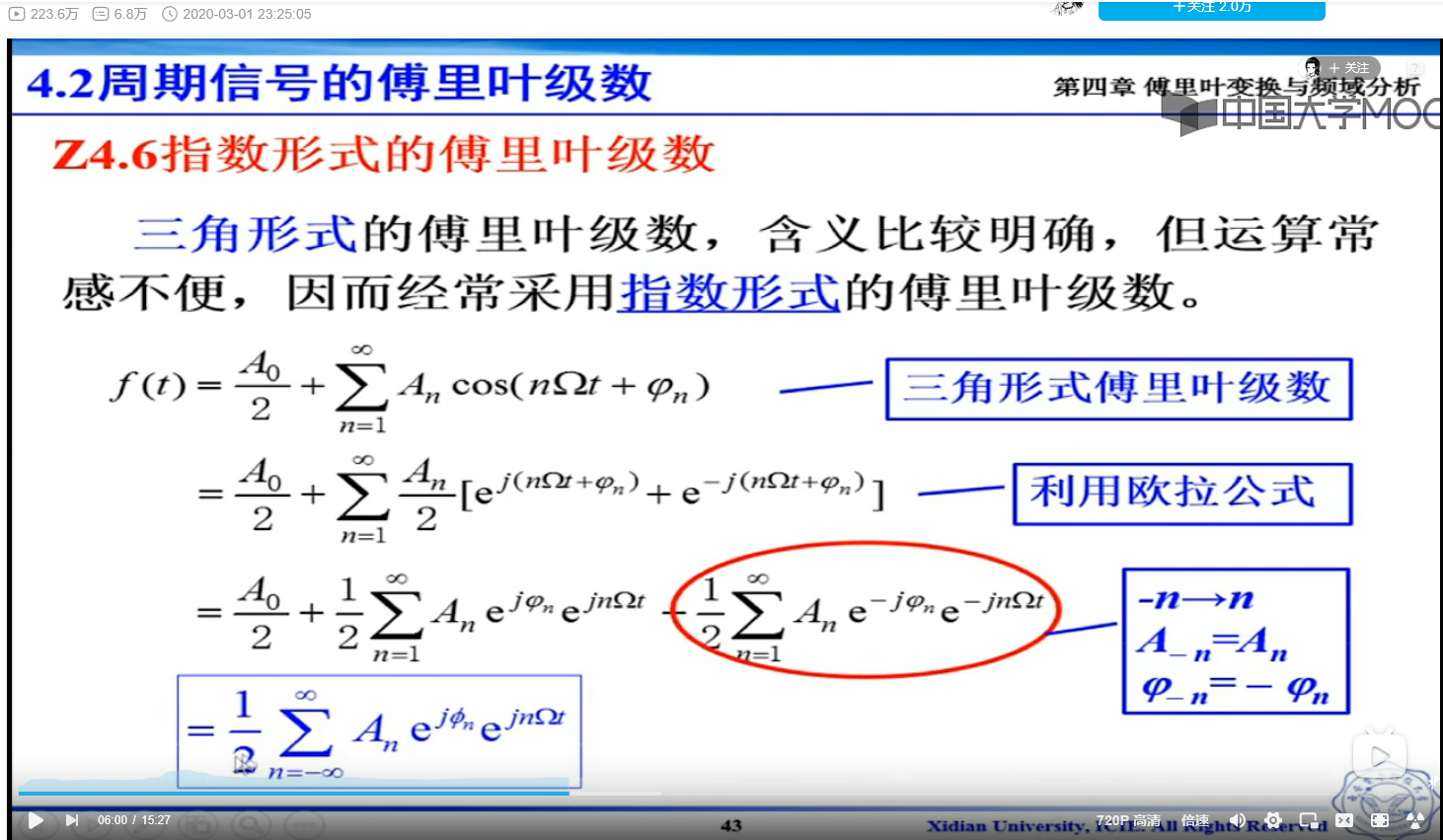
傅里叶变换这其实是两个函数的合成函数，把其中一个变量替换成n, 变量替换后，转啊换为了这个形式

 

 

 

91

 

 

 

 

 

 

 

 

 

 

 

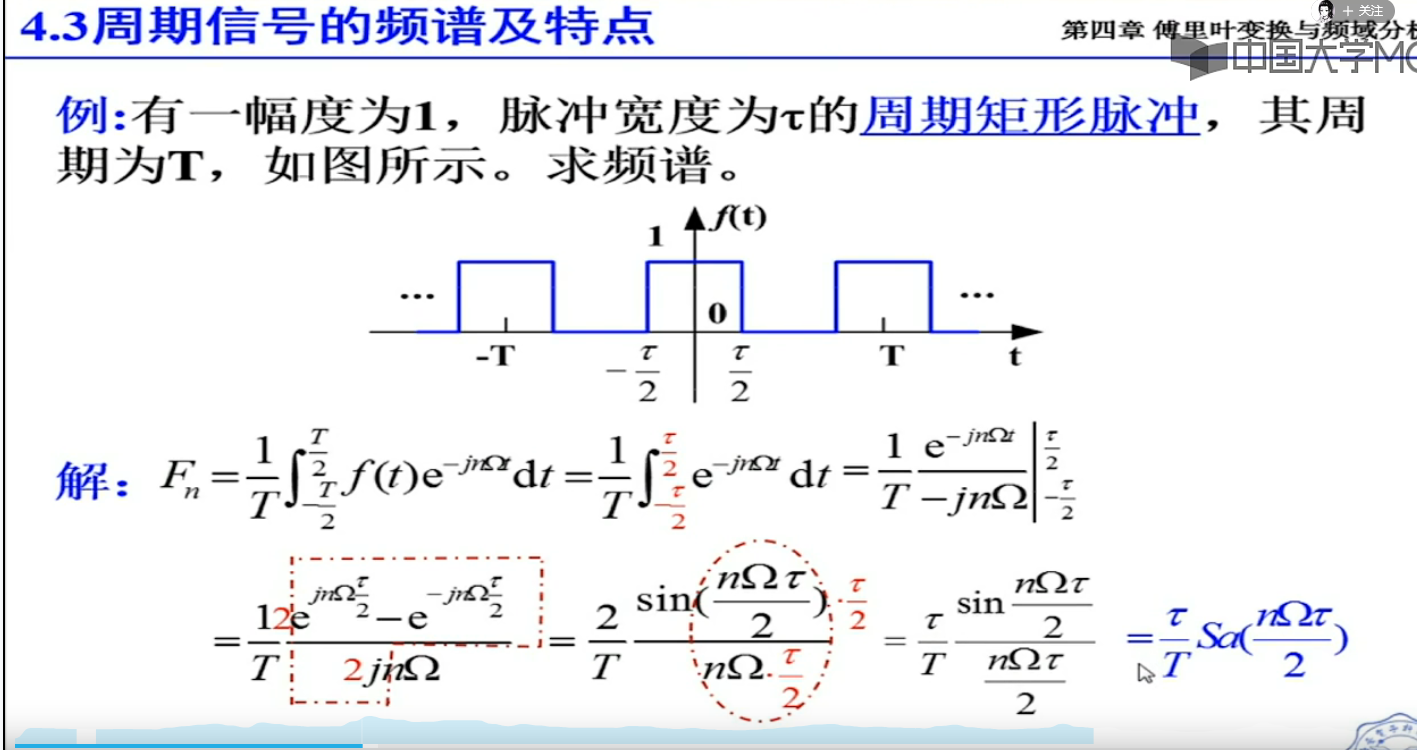
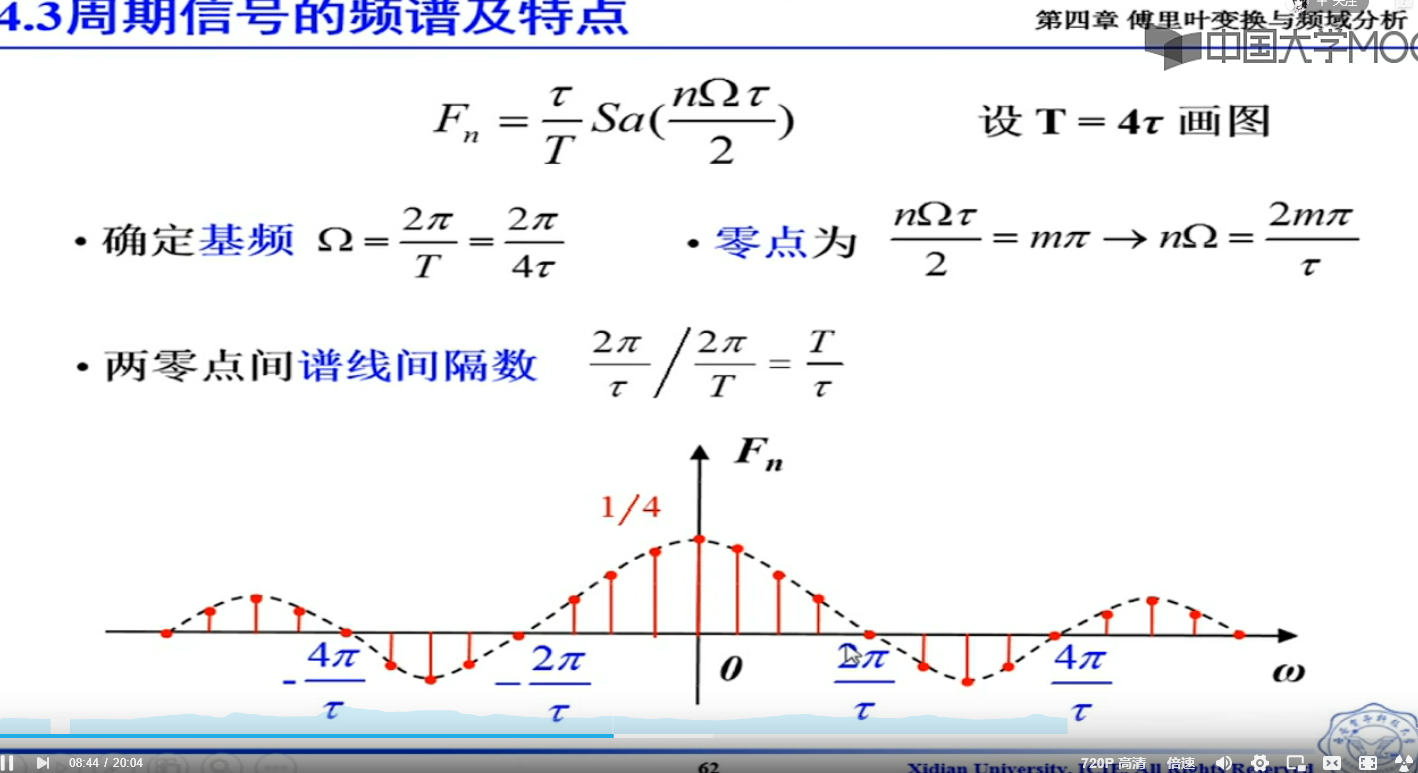
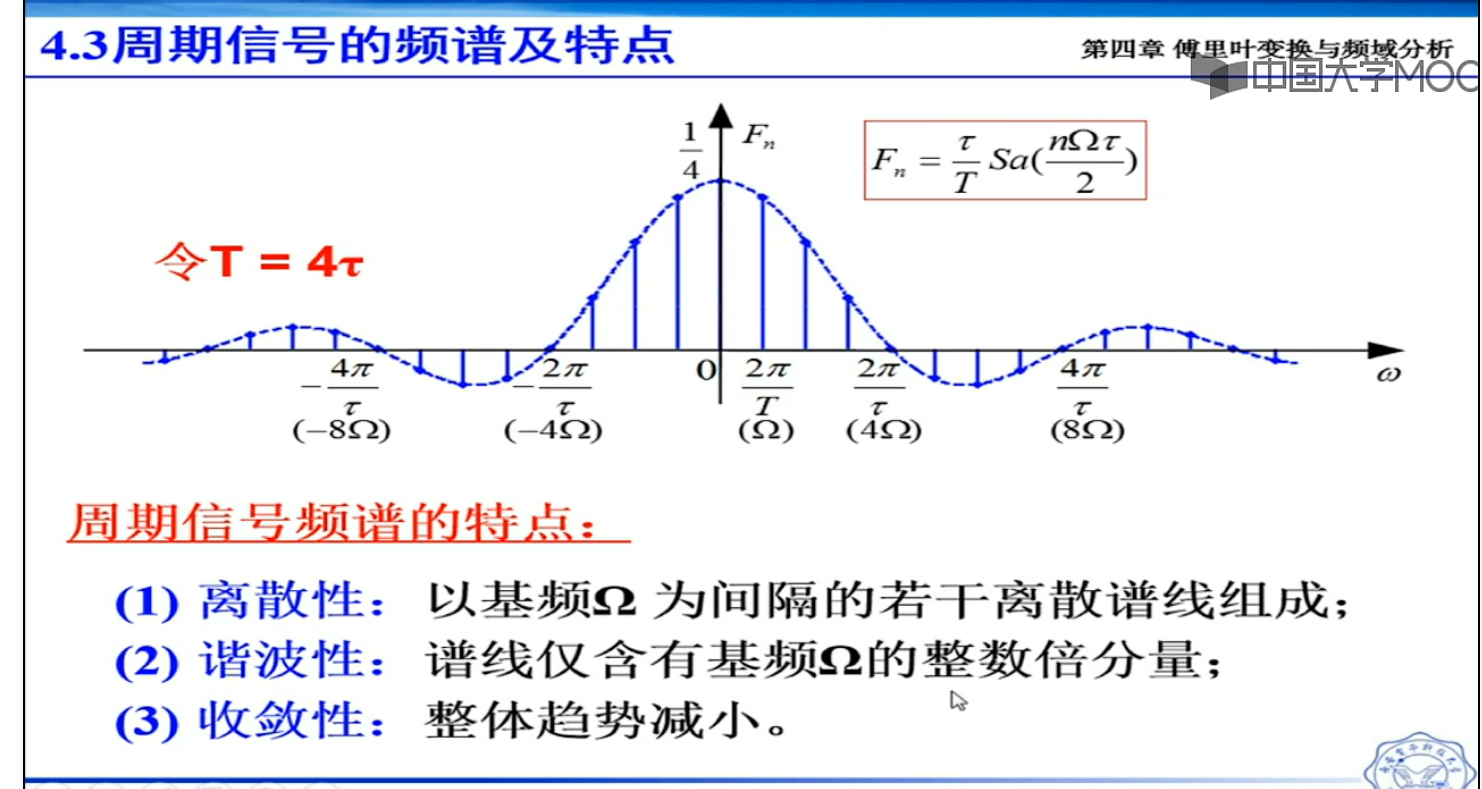
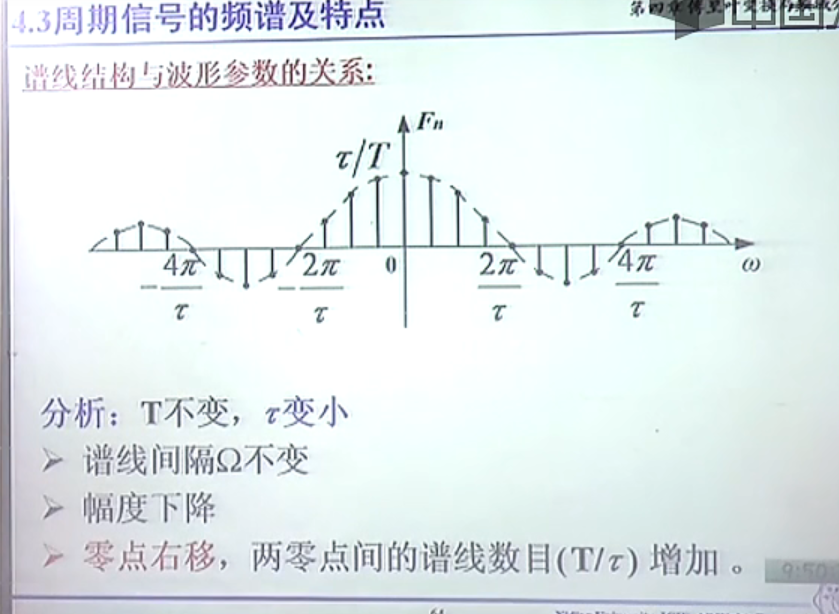
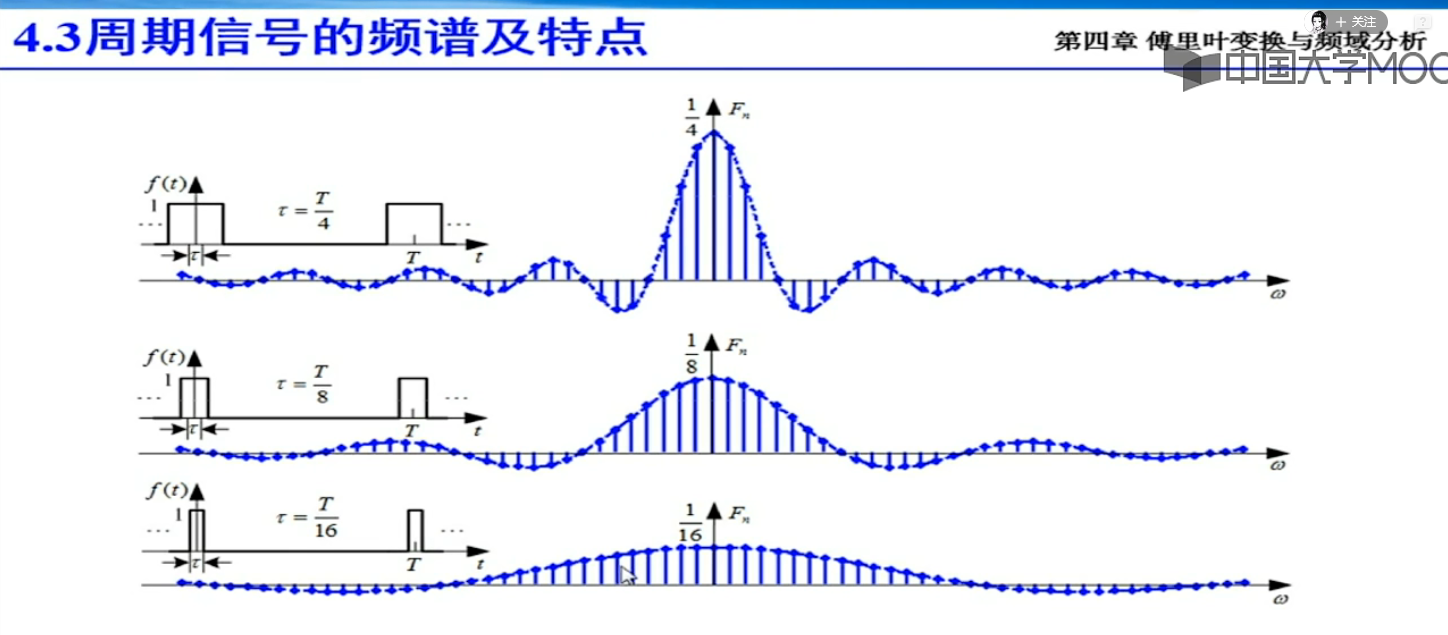
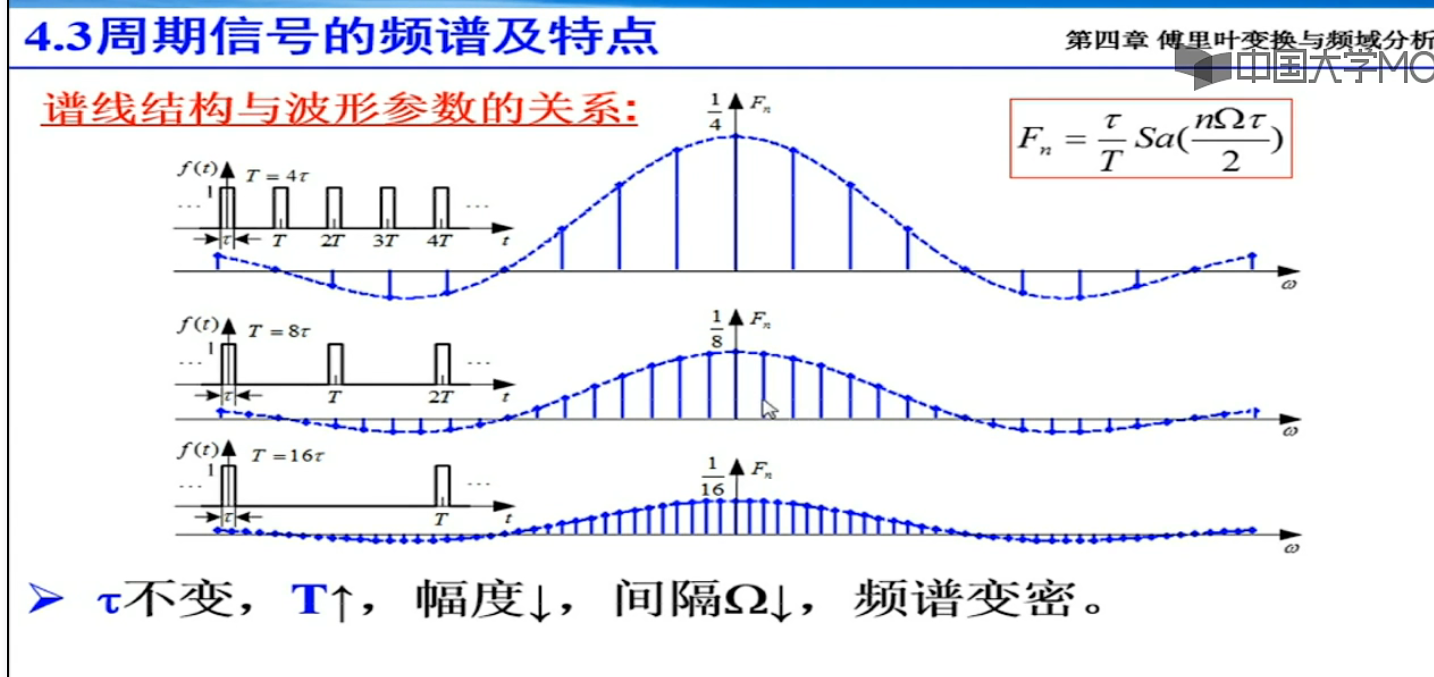
 当T-oo，谱线变成连续的，这就变成了傅里叶变换

 

 

 

 

 

 

 

 

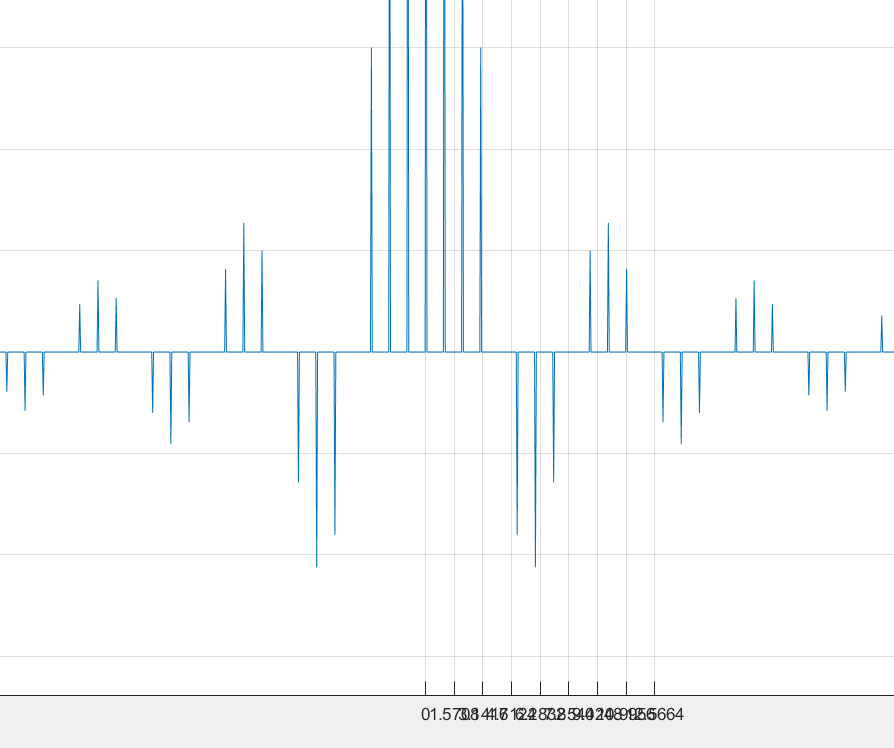
电流的有效值是根下i方/2,电流的有效值就是i/根下2

 

 

 

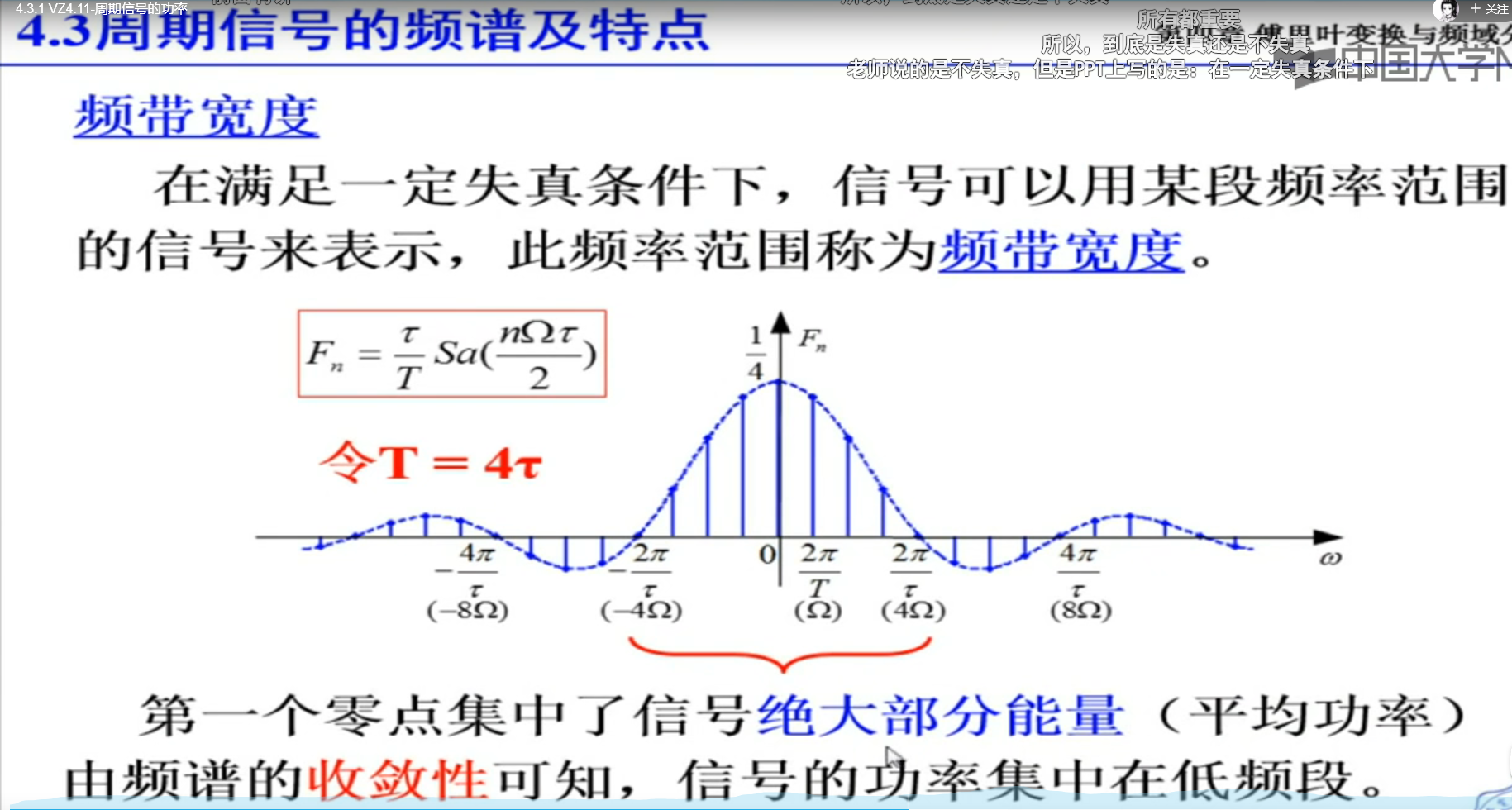
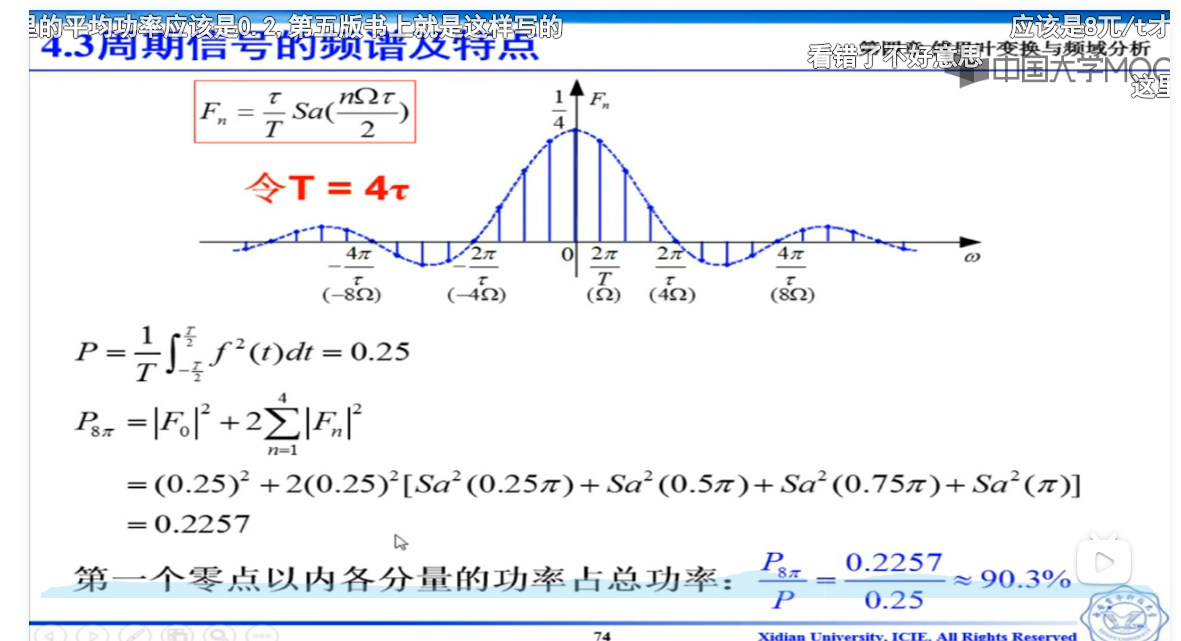
的nw和f，是角速度和频率两个维度，互相转化

 

 

傅里叶变换，是点对点的变换对，可以理解成两个空间的对应变换

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

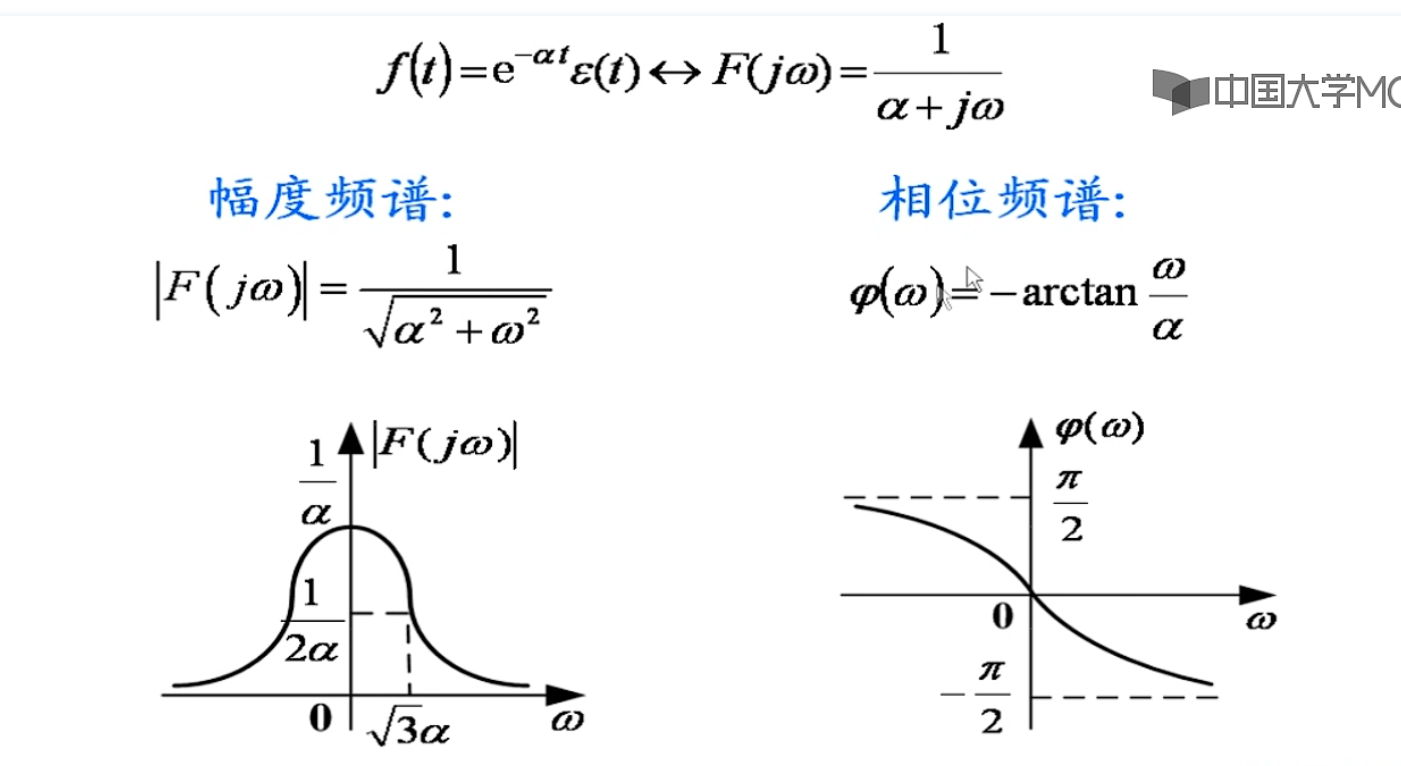
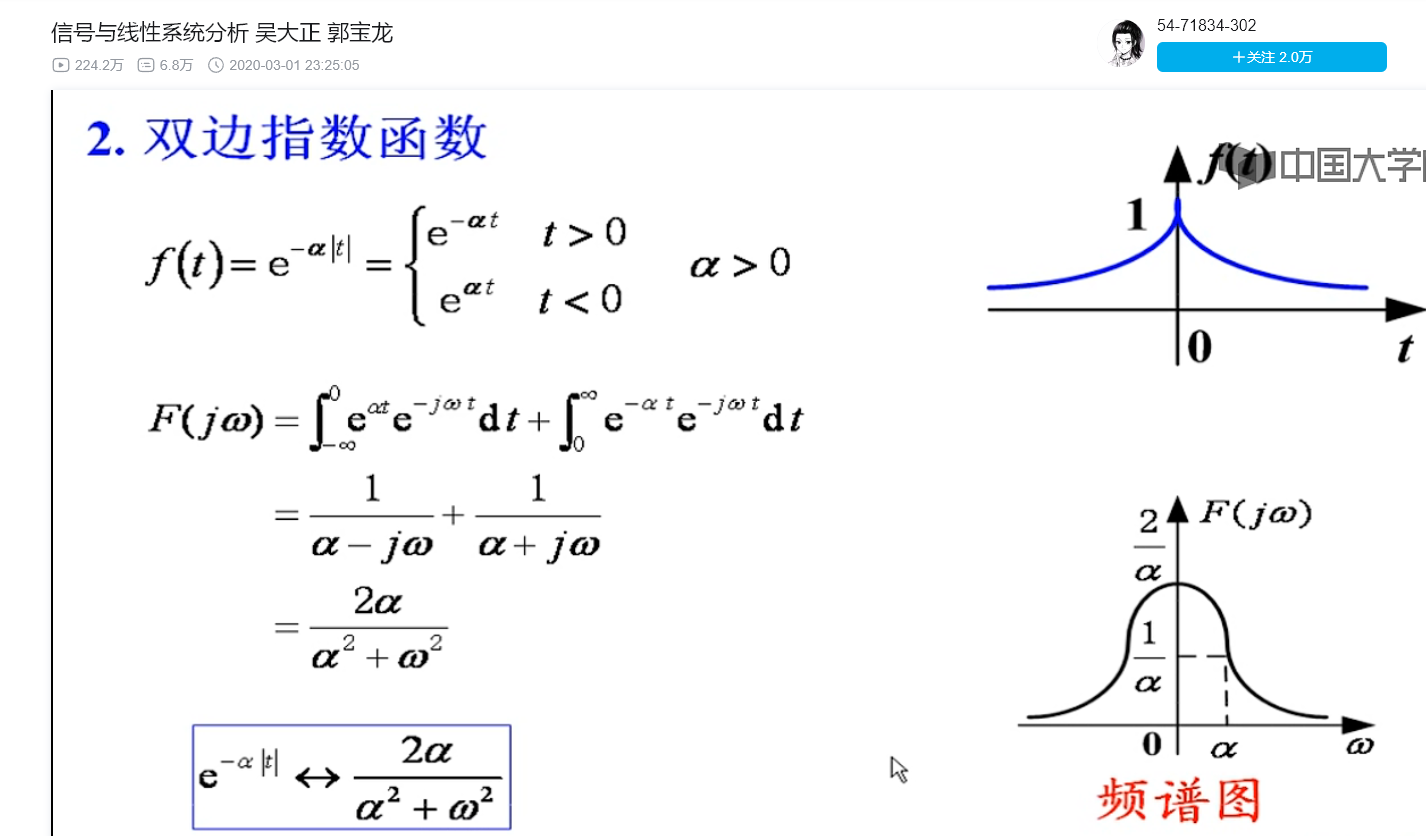
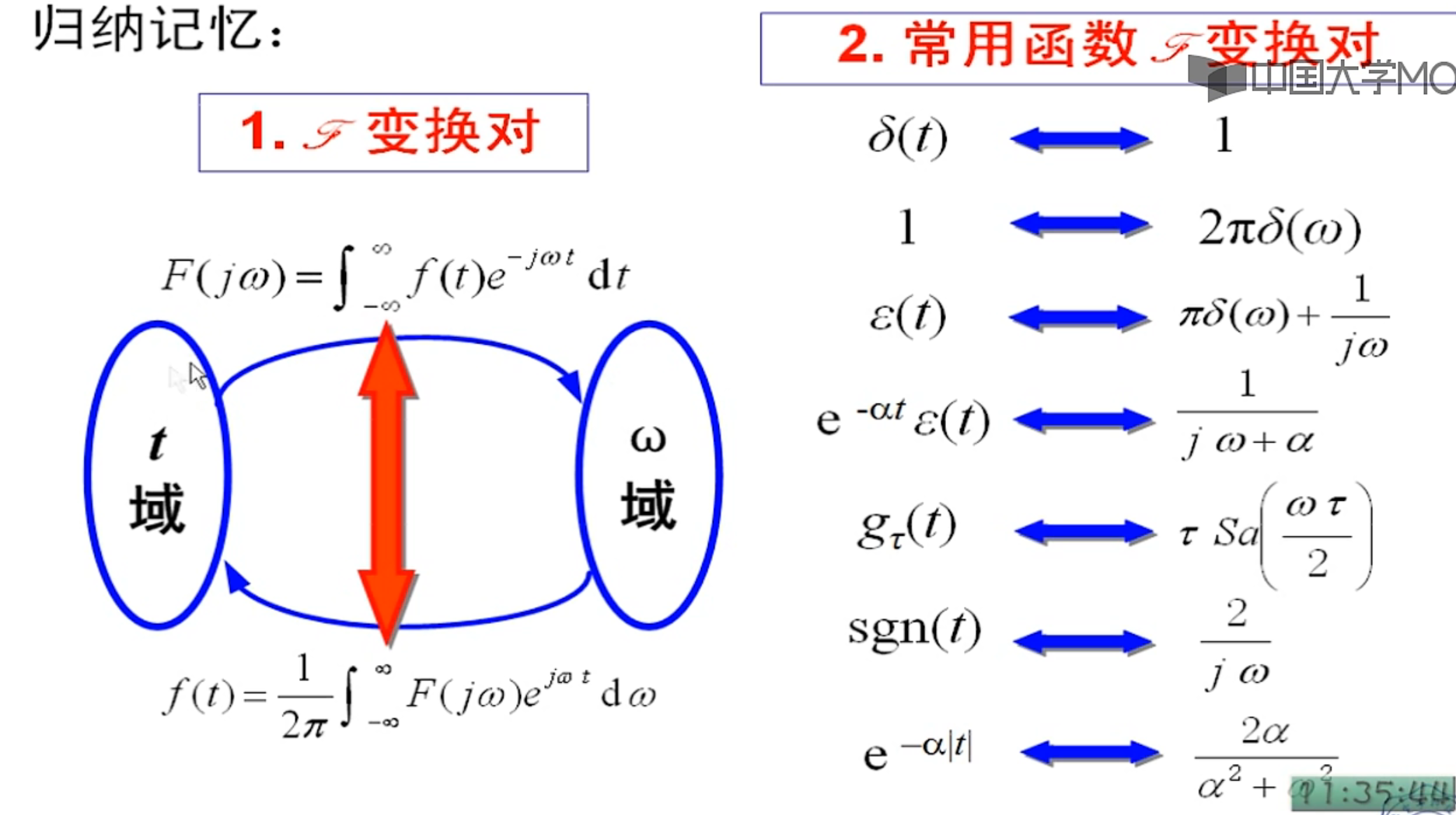
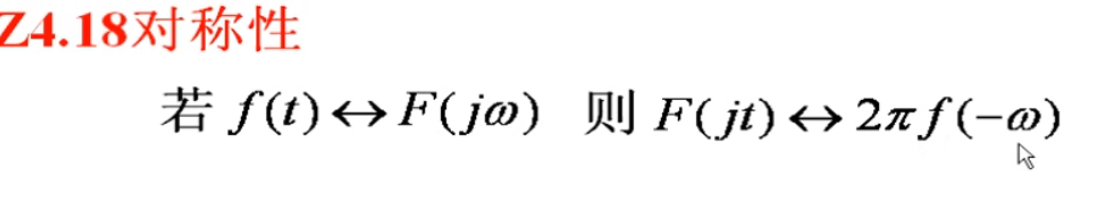
换两次，就成了另外一对

 

 

106

 

 

 

 

 

 

 

 

 

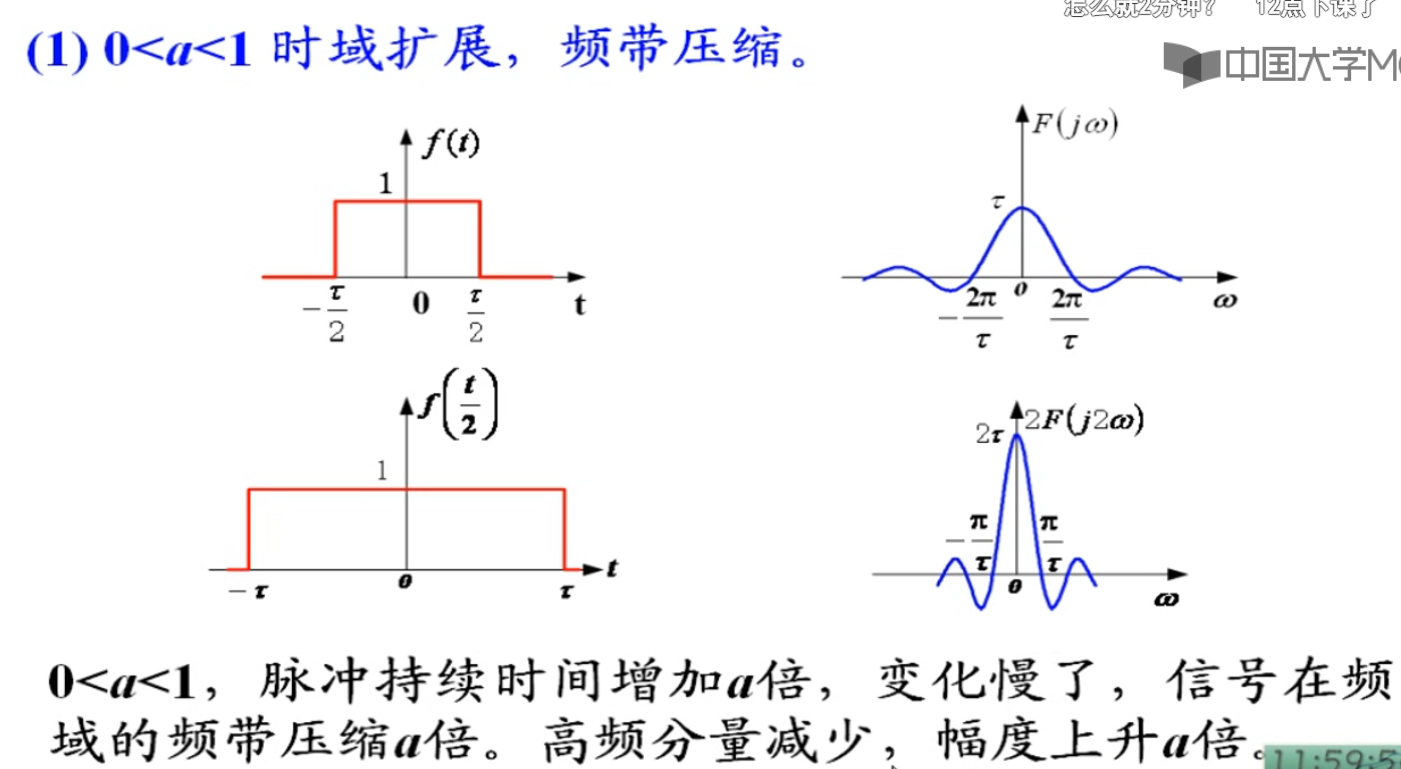
这个性质可以用来分析振动的传导

 

 

 

 

 

把信号变成复数信号，再搬移

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

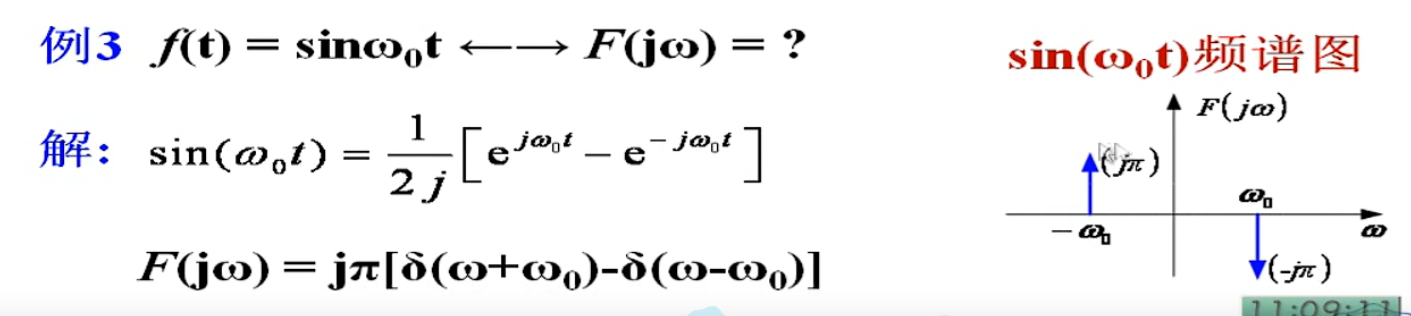
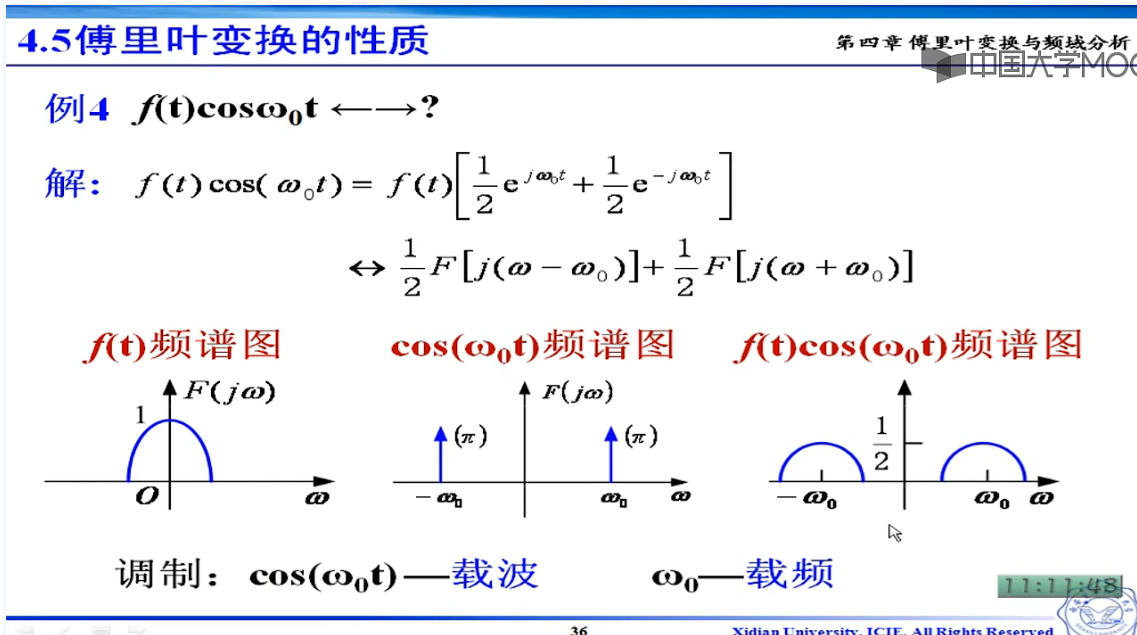
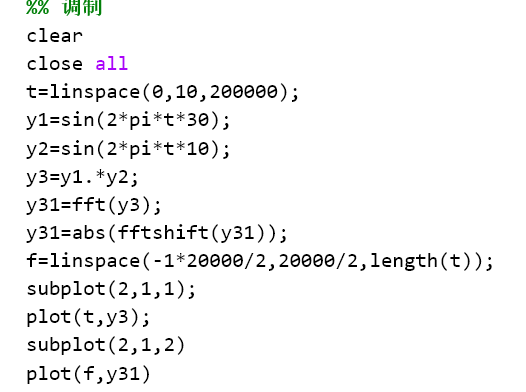
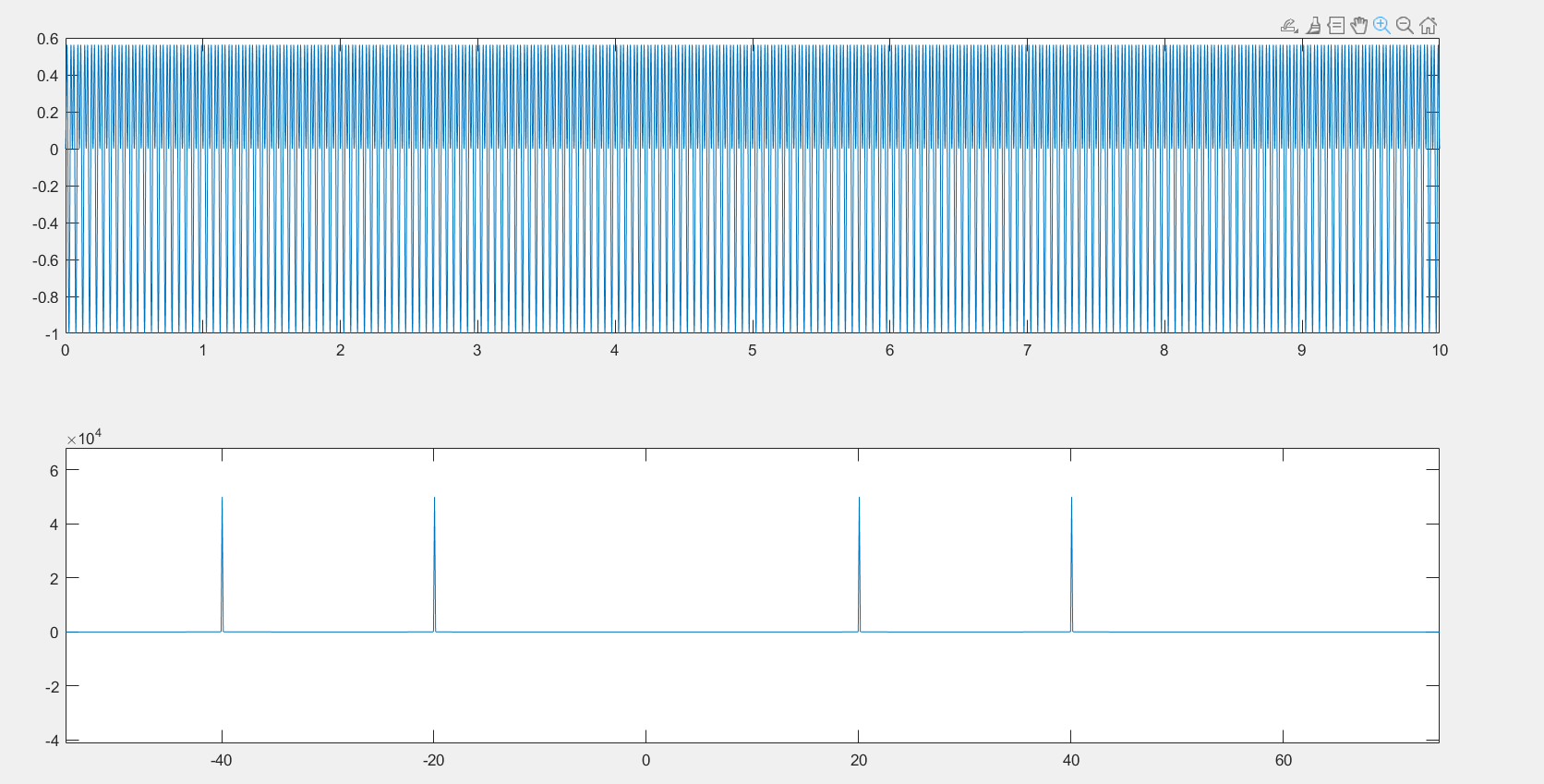
 搬运后，原来的频谱左右平移了10hz

同步解调，再想成，中间形成原来的波形

时域相乘，频域相卷，卷积后，等于搬运了原来的频频，搬运两次，第二次就相当于解调

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

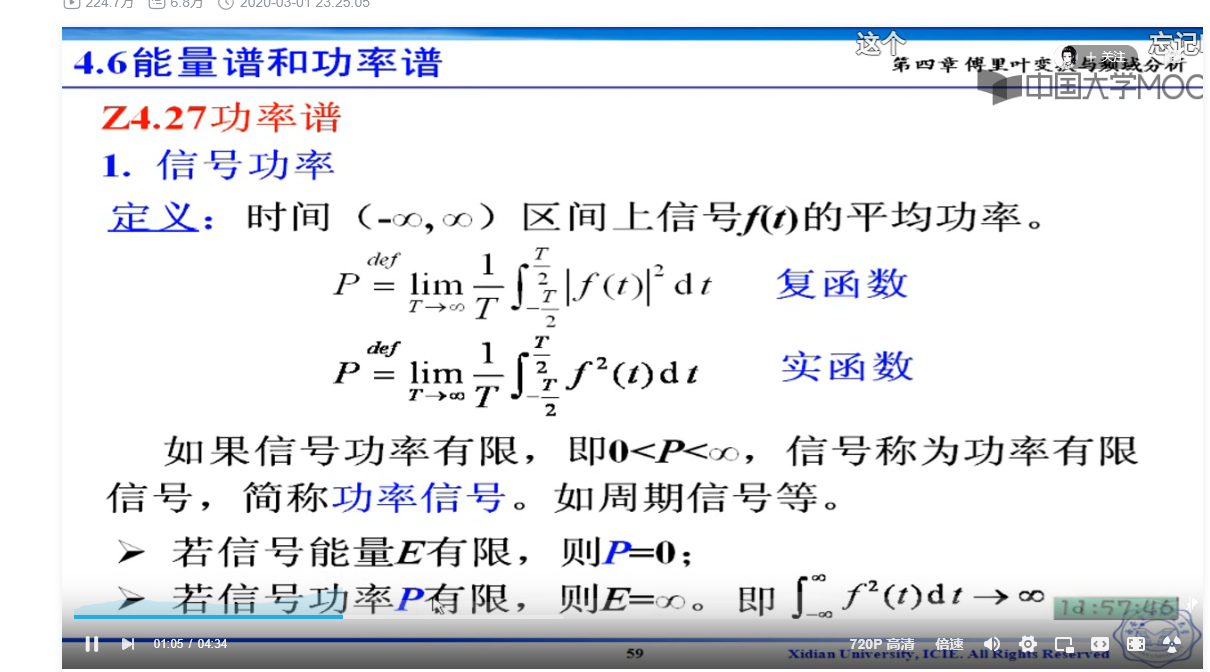
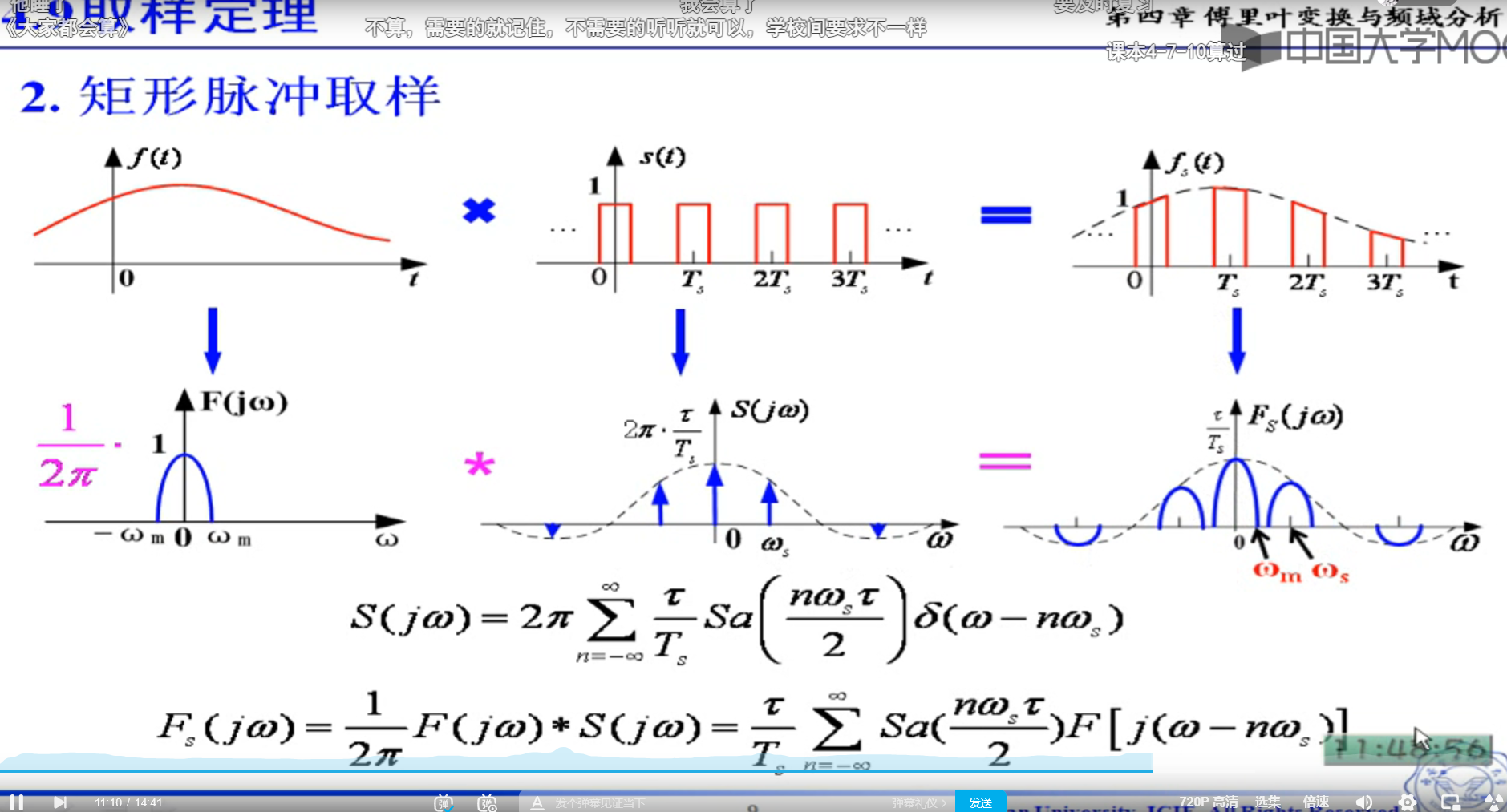
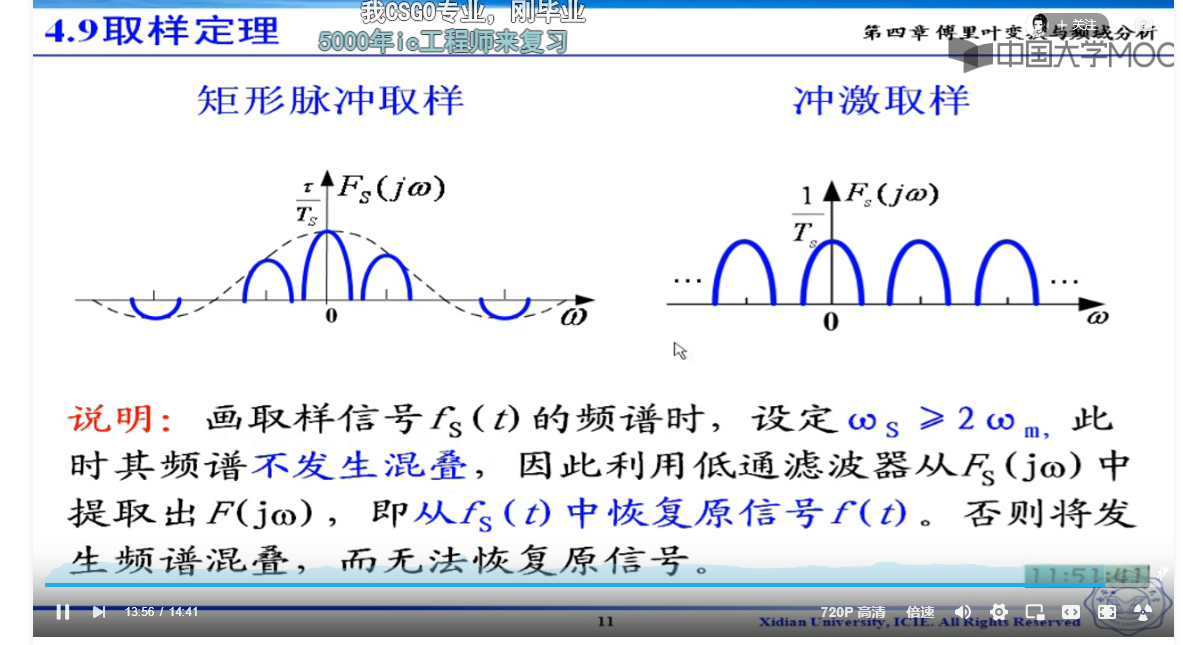
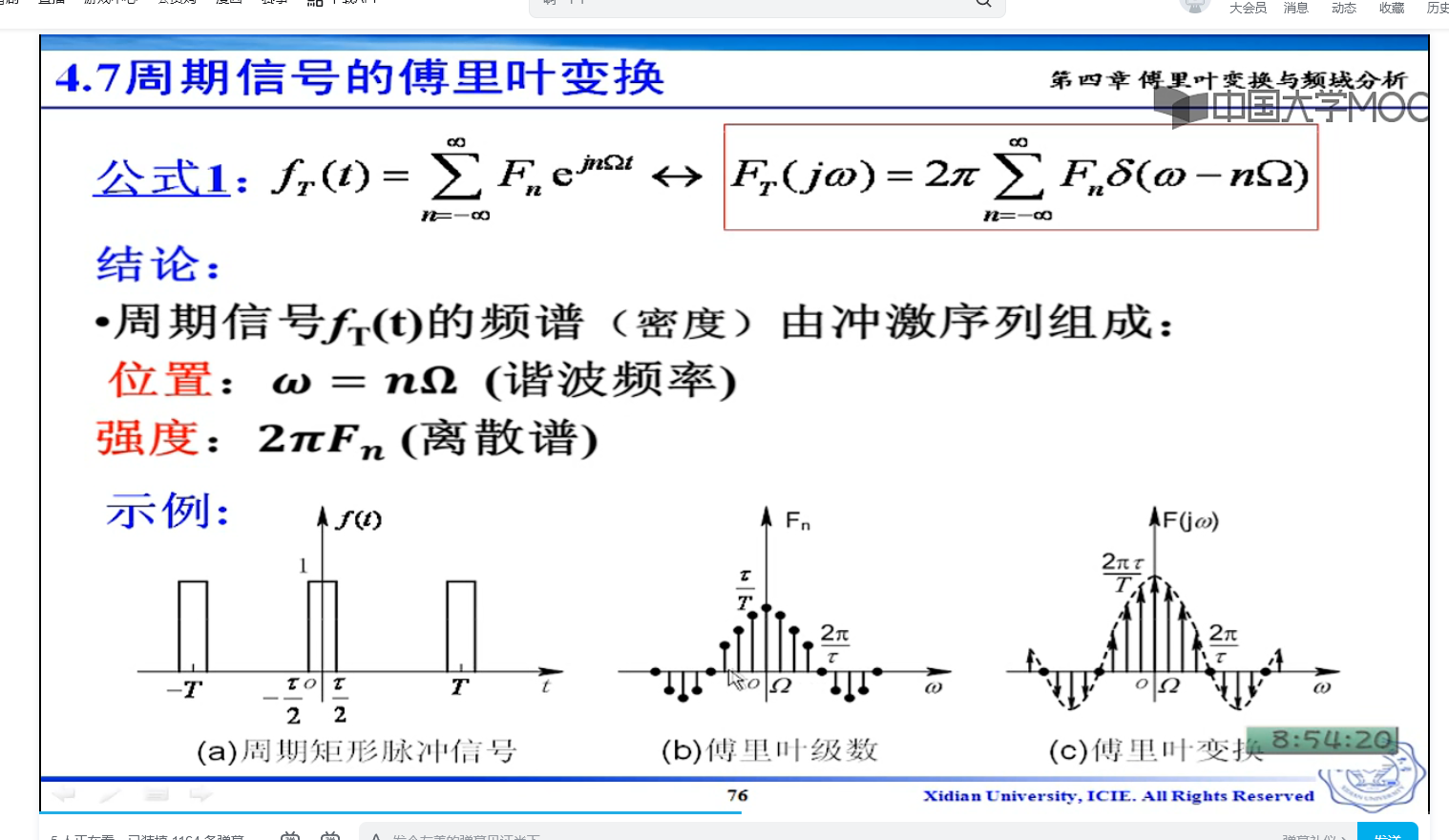
 阶段的信号，相当于一个有限的周期

 

 

 

 

 

 原来的fn乘以delta，和2pi

 

115

 

 

 

 

 

 

 

 

 

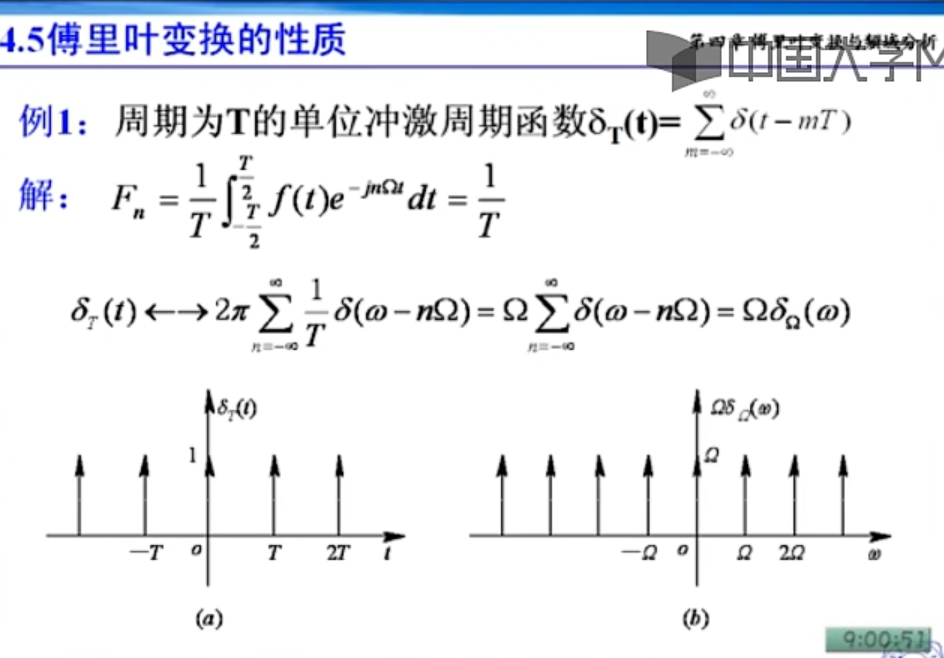
 这个公式，知道了傅里叶变换，也可以求傅里叶级数

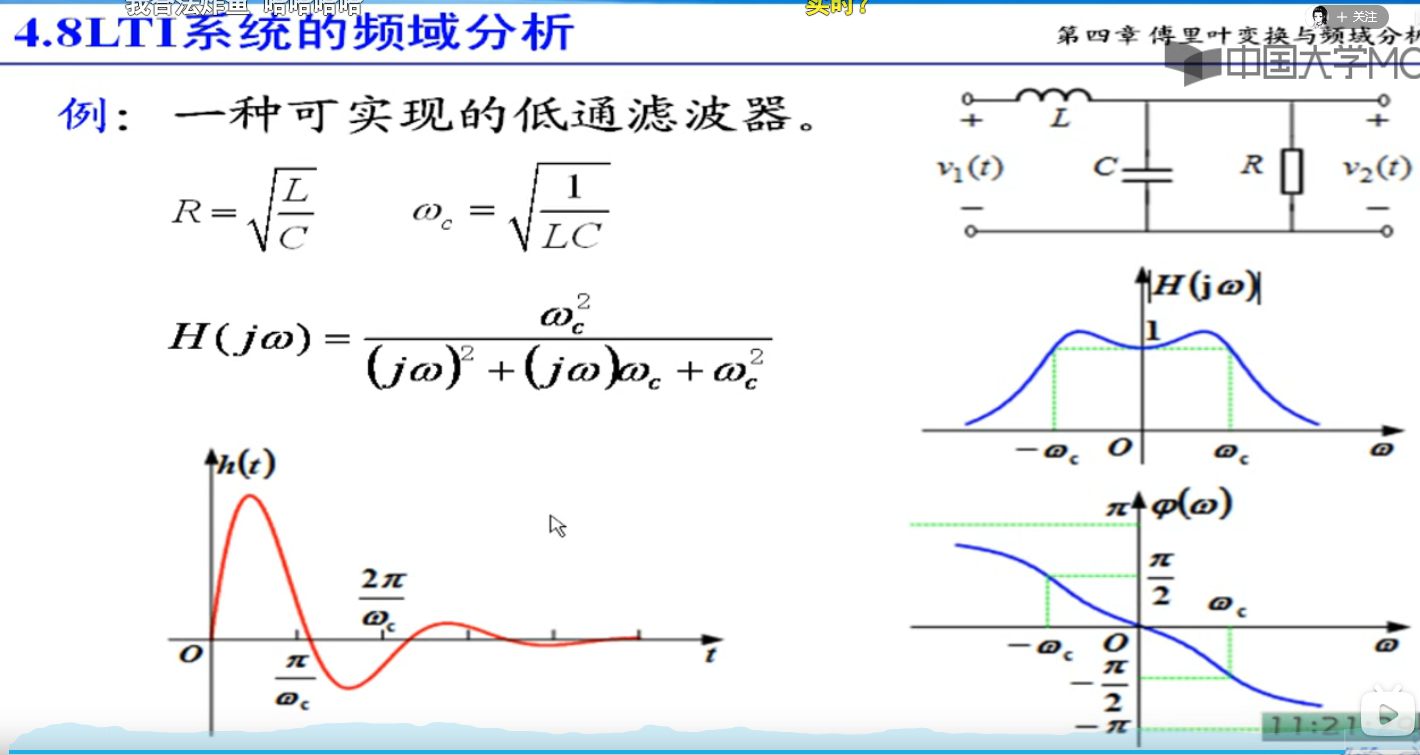
有可傅里叶变换，就可以求解系统再频域里的响应，思路和时域一样，先全求单位频域信号的响应，然后再合并

 

 

 

 

 

 

 

 相当于，基本信号过去lti后，还是原来的频率，不过相位和振幅变化了，基本信号是不变得

 

 

 

 

 

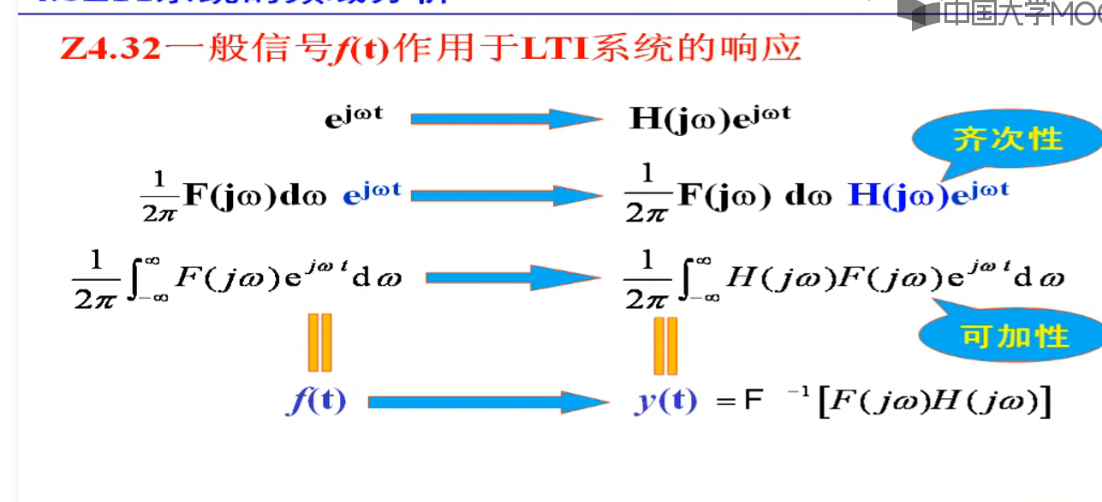
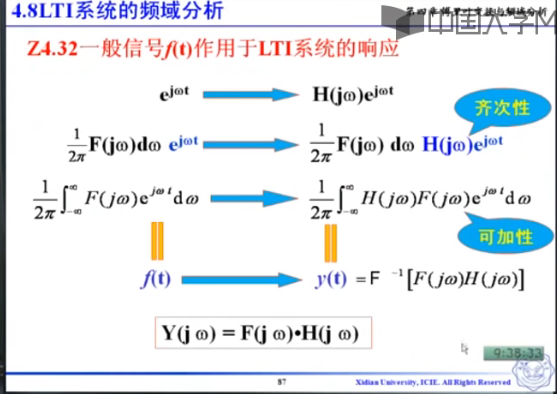
频域分析的核心

 

 

 

 

 

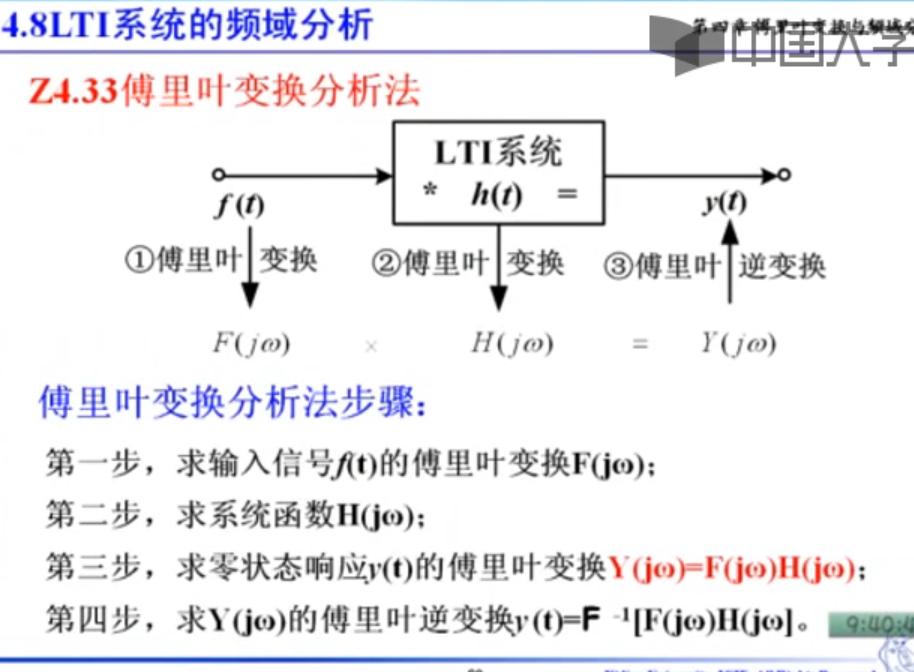
 周期信号，就是fn*标准信号*H(JW)

 

 

 

 

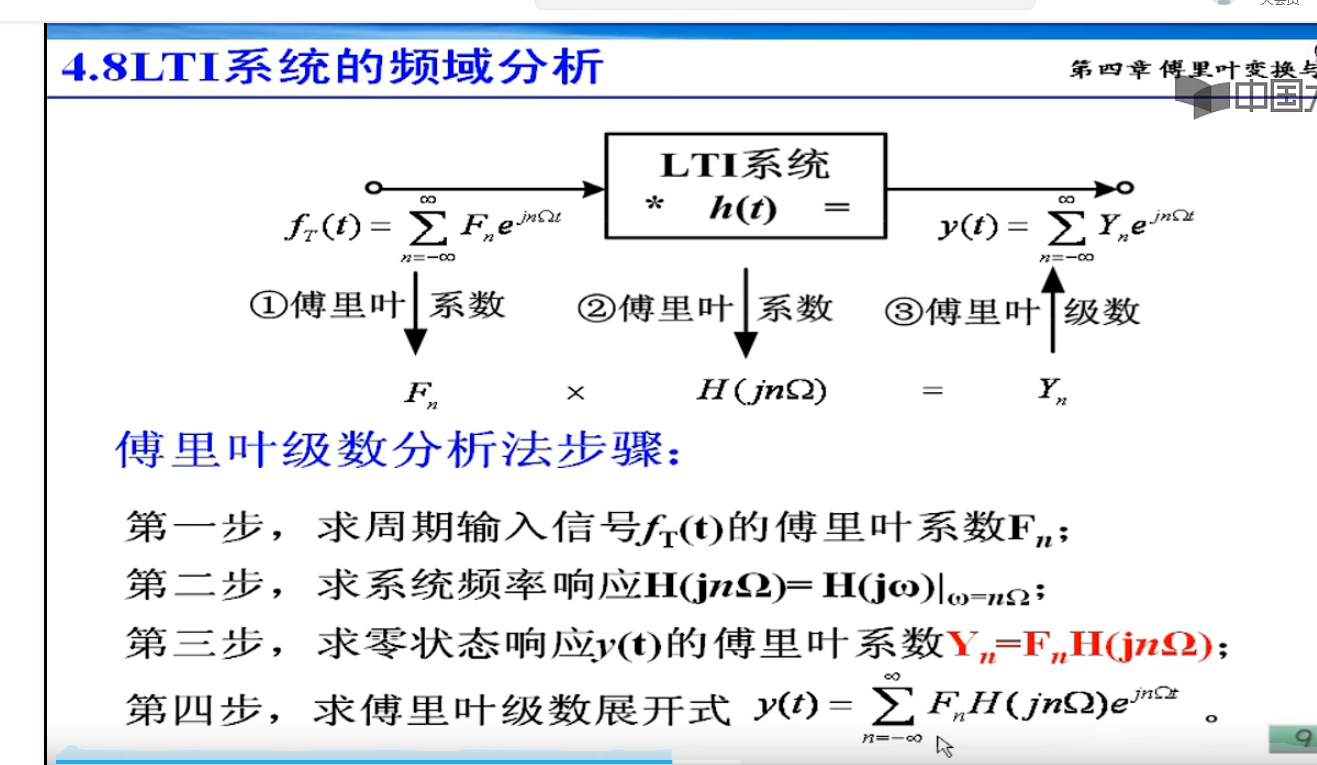
信号通过系统，频率不变，幅度和相角变化，受H(W)的控制

 

 

 

 

用得就是这个公式，信号乘以幅度响应和角度响应

 

 

 

 

 

 

 

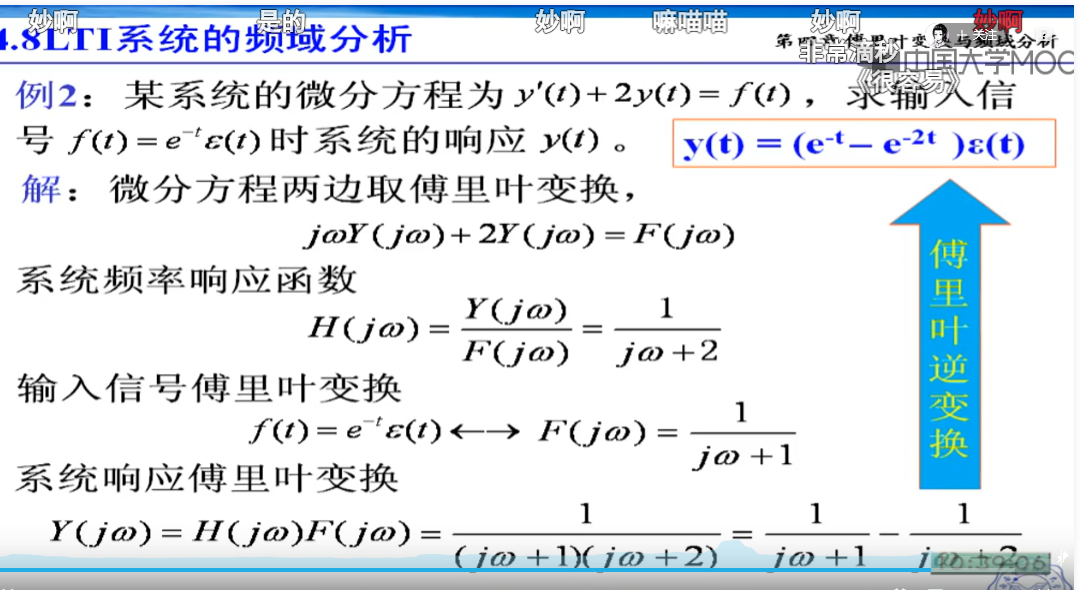
 传输函数反应了系统的特性，传递函数和输入输出无关

 

 

 

 

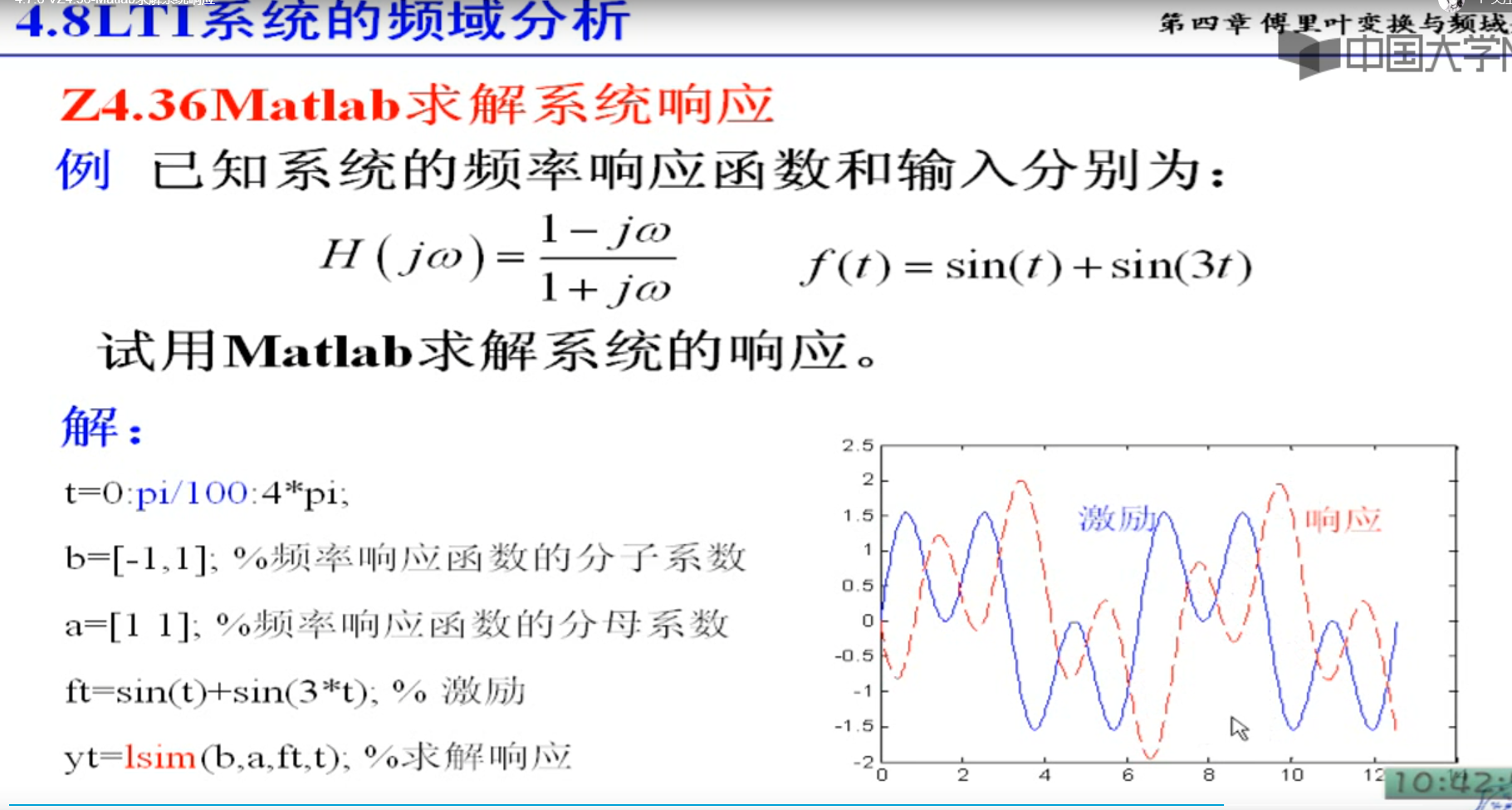
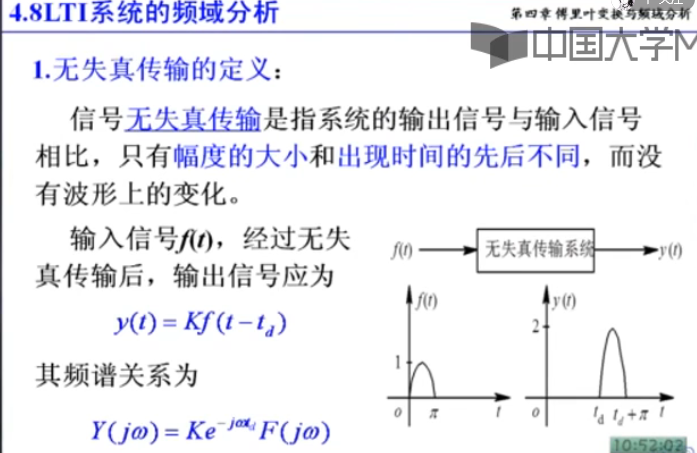
 不失真的条件是幅度是直线，角度是斜线，角度延迟同一时间，所有频率越高，角度越大

 

 

 

 

 

 

 122

 

 

 

 

两个必须满足一个

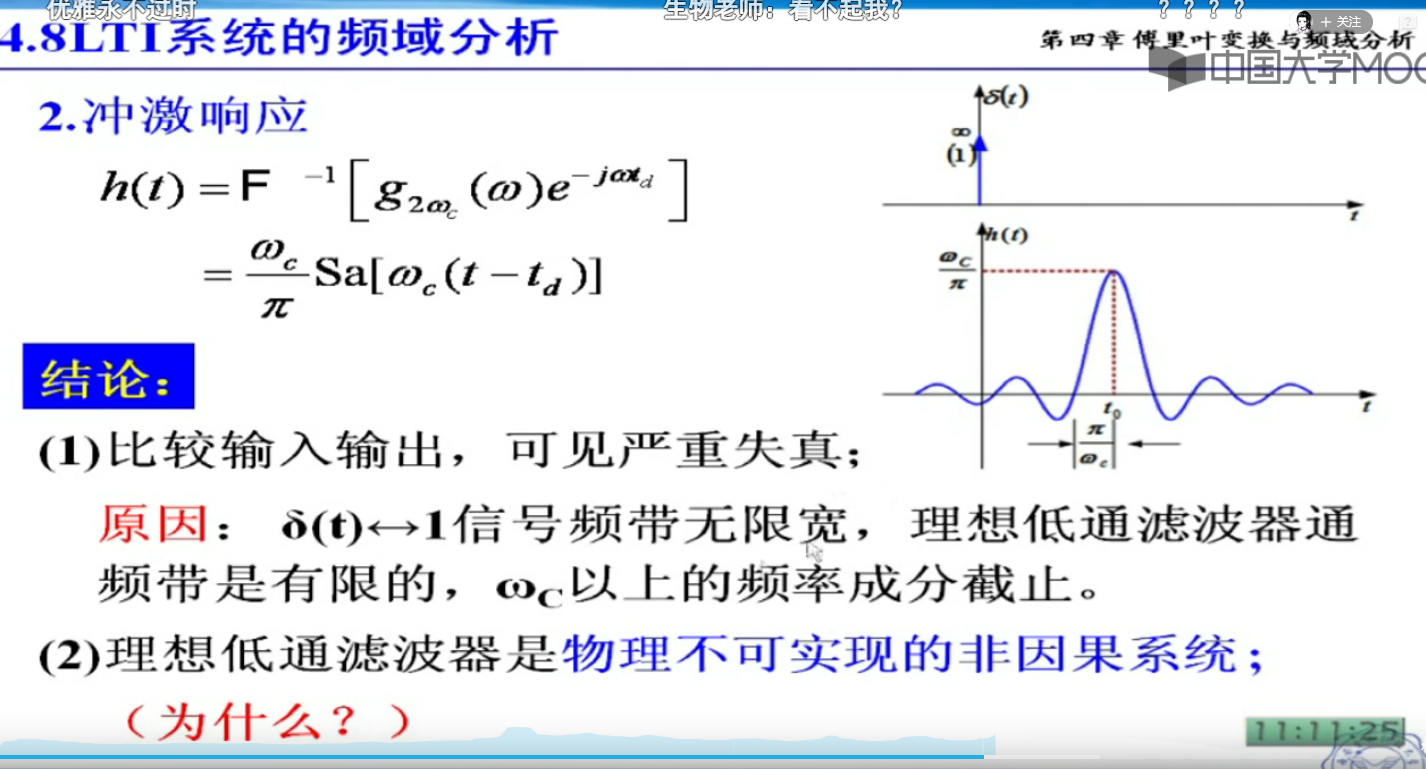
频率响应不能有0，否者就无法物理实现

 

 

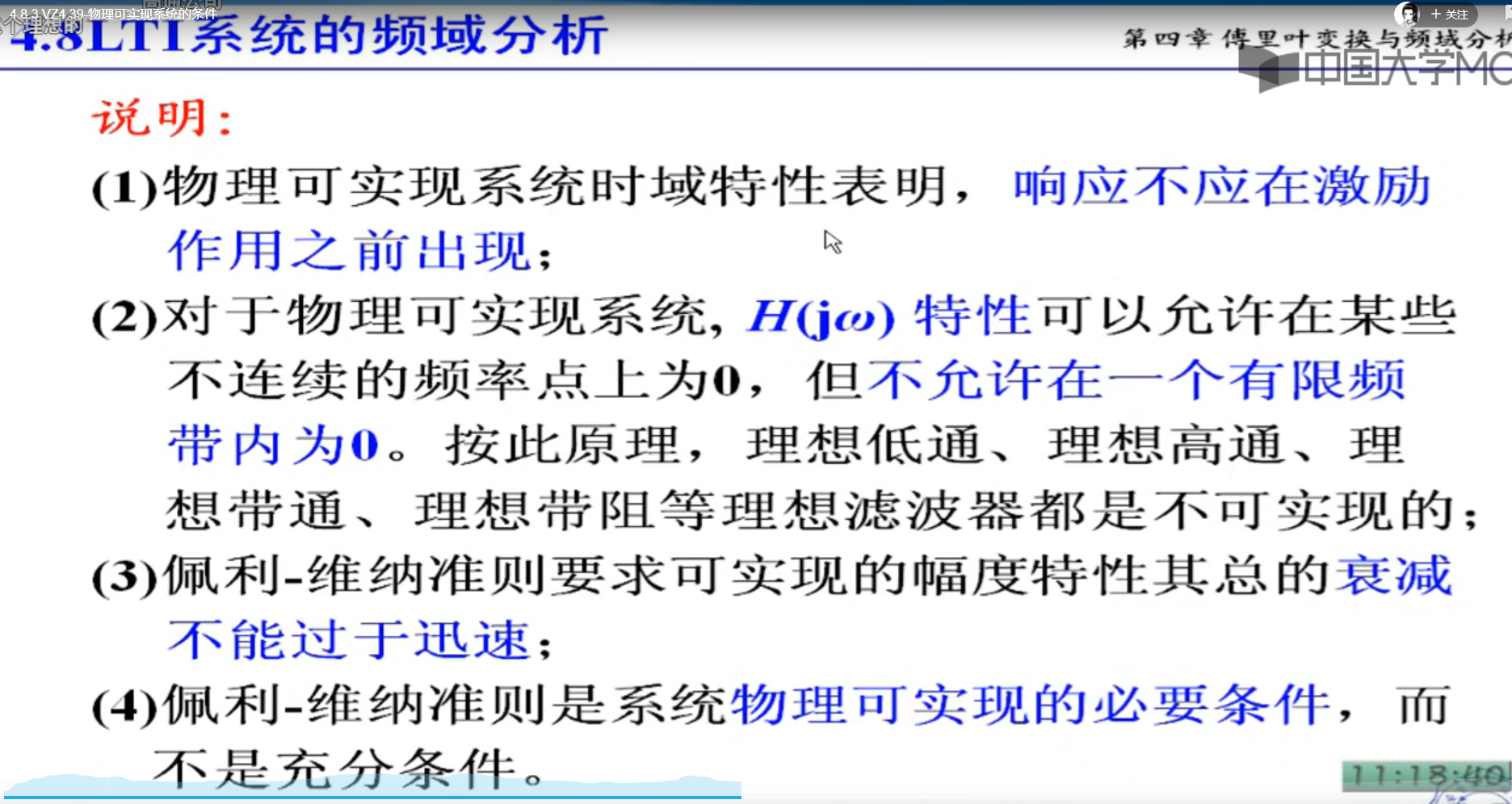
这是 必要条件，满足了，也未必一定能物理实现