砝码称重问题
2012-08-17 17:18 coodoing 阅读(4244) 评论(0) 编辑 收藏 举报1、问题描述
问题1、如果天平两端都允许放砝码,并且假定所有的砝码都是整数克。为了称出从 1 克到 40 克所有整数克的物品,最少需要几个砝码?
问题2:4个砝码,每个重量都是整数克,总重量为40克,放在天平上可以称出1~40克的物体。编程求出这4个砝码各多少克。
2、 问题分析
2.1、问题1分析(砝码称重问题,因式分解有妙用)
秘密在于 3 的幂
说起来这个问题历史还算是挺悠久的。据《数学游戏与欣赏》( [英] 劳斯·鲍尔 [加] 考克斯特 著,杨应辰等 译),这个问题被称作巴协 (Bachet) 砝码问题;而据《数学聊斋》(王树禾著),该问题至少可追溯到 17 世纪法国梅齐里亚克 (Meziriac, 1624) 。他们给出的答案是:最少需要 4 个砝码,规格分别为 1 克、3 克、9 克和 27 克。
例如,为了称出 2 克的物品,我们只需在天平一端放 3 克砝码,在另一端放上 1 克的砝码;而要称出 7 克的物品,则可以在一端放上 1 克和 9 克的砝码,另一端放上 3 克的砝码。
类似地,要称出 1 克到 4 克中所有整数克的物品,只需要 2 个砝码;要称出 1 克到 13 克中所有整数克的物品,则只需要 3 个砝码;要称出 1 克到 121 克中所有整数克的物品则要 5 个砝码,它们分别是 1 克、3 克、9 克、27 克和 81 克,如此等等。
也许有人已经心领神会了,但是如果就此满足而匆匆离去的话,可能就错失了一个领略数学思想的机会——问题到这里并未结束啊!例如,4 个砝码究竟是不是最少的?还有没有其他的组合?对这些疑问的一个彻底的分析和说明,是 19 世纪由麦克马洪 (MacMahon) 给出的。下面就来领略一下其中的思想吧,或许你会从中学到很多。
因式分解的妙用
假设有一个重为 a 克的砝码,那么用它自然能够称出 0 克和 a 克的物品。不过,如果虚设天平的某一端为正的话,利用此天平和砝码我们还能称出 - a 克的物品——不妨规定把 a 克砝码放在天平右侧,将物品放在天平左侧,由此可以称出 a 克的物品;但若把 a 克砝码放在天平左侧,把物品放在天平右侧,由此称出的物品重量记作 - a。目前这样一种设想有点怪异,但这实际上和人类引入负数的思想是相同的。很快大家便会发现,这种设定非常精妙地简化了我们的计算和推导。现在暂且把该砝码能够称出的重量 - a,0,a 放进一个表达式中:
现在,假设有两个不同规格的砝码,分别重 a 克和 b 克(a < b)。按照上面的规定,我们可以称出 - a - b ,- b,- a,a - b,0,b - a,a,b,a + b。例如,为了称出 b - a,只需要把 b 克的砝码放在右端,物品和 a 克的砝码放在左端;按照上面的约定,如果天平平衡,物品就是 b - a 克。而要称出 a - b, 则把 b 克砝码放在左端,a 克砝码和物品放在右端,如果平衡则物品是 a - b 克。同样地,把这些数塞进一个表达式:
可以看到,它不是别的,正好是
的展开式。
另外,假设有 m 个同样重为 a 克的砝码,则可以称出 - ma,- (m - 1)a,…,0,…,(m - 1)a,ma 克的物品。暂且按照上面的办法,把这些数也塞进一个表达式中 :
结合上面的分析,容易看出,如果有 m 个 a 克的砝码,n 个 b 克的砝码,等等,那么可以称出物品的克数就是表达式
展开后出现过的那些 x 的幂数,而展开式中 x 的 i 次项系数就表示用给定的这组砝码称出 i 克物品的不同方法数。
如果要称出 1 到 40 中所有的整克数,并且要求所用的砝码尽可能少,我们自然希望这些砝码能够“物尽其用”,称出的克数正好都是我们需要的克数,并且称的方法都是唯一的。也就是说,上述表达式展开后应该恰好是
反过来,就是要把
的形式。
对这个式子进行分解,一共有八种不同的方案:
前四个式子展示了我们实际上是如何对原式进行逐步分解的。它们的意义依次为:(1) 40 个 1 克的砝码;(2) 1 个 1 克,13 个 3 克的砝码 ;(3) 1 个 1 克,1 个 3 克以及 4 个 9 克的砝码;(4) 1 个 1 克,1 个 3 克,1 个 9 克以及 1 个 27 克的砝码。其中,第四个分解式是最基本的,它就是我们想要的答案。
2.2、问题2分析
设4个砝码的重量分别为w1、w2、w3、w4,则w1+w2+w3+w4=40,且w1,w2,w3,w4均为正整数。假设不相等(假设w1<w2<w3<w4),故砝码中最大为34克。称重的天平有物体盘和砝码盘,称重时:
- 若砝码只放在砝码盘,则物体质量=砝码盘砝码质量;
- 若砝码盘和物体盘中都放置了砝码,则物体质量=砝码盘砝码质量-物体盘砝码质量。
从1~40,任意一个数,都应该能找到相应的砝码放置方法。砝码只有4个,且每次称重时,这4个砝码只能出现0次或者1次,且砝码要么在物体盘,要么在砝码盘,要解该问题,应该转换思路。
- 假设砝码在物体盘,认定其出现-1次;
- 假设砝码在砝码盘,认定其出现1次;
- 若该次称重,不需要该砝码,认定其出现0次。
设4个砝码在每次称重中出现的次数分别为x1,x2,x3,x4,则只有-1、0、1这三种取值。如上分析,找到的砝码组合个数应该为40个(即1~40中的任意一个数都有对应的砝码组合)。
3、具体实现
1: namespace WeightProblem
2: {
3: class Program
4: {
5: //砝码总重量
6: const int TOTALWEIGHT = 40;
7:
8: //4个砝码,w1+w2+w3+w4=40,且w1,w2,w3,w4均为整数,假设不相等(假设w1<w2<w3<w4)故最大为34
9: const int MAXWEIGHT = 34;
10:
11: static void Main(string[] args)
12: {
13: int w1, w2, w3, w4;
14: for (w1 = 1; w1 <= MAXWEIGHT; w1++)
15: {
16: for (w2 = w1 + 1; w2 <= MAXWEIGHT; w2++)
17: {
18: for (w3 = w2 + 1; w3 <= MAXWEIGHT; w3++)
19: {
20: for (w4 = w3 + 1; w4 <= MAXWEIGHT; w4++)
21: {
22: if (w1 + w2 + w3 + w4 == TOTALWEIGHT)
23: {
24: if (weight(w1, w2, w3, w4))
25: {
26: System.Console.WriteLine("w1={0} w2={1} w3={2} w4={3} ", w1, w2, w3, w4);
27: output(w1, w2, w3, w4);
28: Console.ReadLine();
29: }
30: }
31: }
32: }
33: }
34: }
35: }
36:
37: //从1~40,不管哪个重量都要找到相应的砝码放置方法
38: //w1,w2,w3,w4分别为4个砝码的重量
39: static bool weight(int w1, int w2, int w3, int w4)
40: {
41: int w; //物体重量
42:
43: //砝码只有4个,且每次称重时,这4个砝码只能出现0次或者1次
44: //出现时,砝码要么在物体盘,要么在砝码盘,要解该问题,转换思路
45: //假设砝码在物体盘,认定其出现-1次
46: //假设砝码在砝码盘,认定其出现1次
47: //若该次称重,不需要该砝码,认定其出现0次
48: //4个砝码在每次称重中出现的次数
49: int x1, x2, x3, x4; //只有-1,0,1这三种取值
50:
51: int count = 0; //找到的砝码组合个数
52:
53: //对1~40中的每个重量,都要找到相应的砝码组合
54: //若有一个w(1<=w<=TOTALWEIGHT)没有找到相应的砝码组合,则表明该组砝码值不是所求
55: for (w = 1; w <= TOTALWEIGHT; w++)
56: {
57: for (x1 = -1; x1 <= 1; x1++)
58: {
59: for (x2 = -1; x2 <= 1; x2++)
60: {
61: for (x3 = -1; x3 <= 1; x3++)
62: {
63: for (x4 = -1; x4 <= 1; x4++)
64: {
65: if (w1 * x1 + w2 * x2 + w3 * x3 + w4 * x4 == w)
66: {
67: count++;
68:
69: //找到该重量对应的砝码组合后,继续下一个重量
70: x1 = x2 = x3 = x4 = 2;
71: }
72: }
73: }
74: }
75: }
76: }
77:
78: //如果找到所有的1~TOTALWEIGHT的砝码组合,则该组砝码值即为所求
79: if (count == TOTALWEIGHT)
80: return true;
81: else
82: return false;
83: }
84:
85: //输出1~40中每个重量对应的砝码组合(负数表示该砝码放在物体盘)
86: static void output(int w1, int w2, int w3, int w4)
87: {
88: int w; //物体重量
89: int x1, x2, x3, x4; //只有-1,0,1这三种取值
90:
91: //对1~TOTALWEIGHT中的每个重量,都要找到相应的砝码组合
92: for (w = 1; w <= TOTALWEIGHT; w++)
93: {
94: for (x1 = -1; x1 <= 1; x1++)
95: {
96: for (x2 = -1; x2 <= 1; x2++)
97: {
98: for (x3 = -1; x3 <= 1; x3++)
99: {
100: for (x4 = -1; x4 <= 1; x4++)
101: {
102: if (w1 * x1 + w2 * x2 + w3 * x3 + w4 * x4 == w)
103: {
104: System.Console.Write("w={0}: ", w);
105: if (x1 != 0)
106: System.Console.Write("{0} ", w1 * x1);
107: if (x2 != 0)
108: System.Console.Write("{0} ", w2 * x2);
109: if (x3 != 0)
110: System.Console.Write("{0} ", w3 * x3);
111: if (x4 != 0)
112: System.Console.Write("{0} ", w4 * x4);
113: System.Console.WriteLine();
114:
115: //继续下一个重量
116: x1 = x2 = x3 = x4 = 2;
117: }
118: }
119: }
120: }
121: }
122: }
123: }
124: }
125: }
4、运行结果
说明:第一行表示4个砝码的质量分别为1,3,9,27;其他行,负数表示该砝码放在物体盘,正数表示该砝码放在砝码盘。
w1=1 w2=3 w3=9 w4=27
w= 1: 1
w= 2: -1 3
w= 3: 3
w= 4: 1 3
w= 5: -1 -3 9
w= 6: -3 9
w= 7: 1 -3 9
w= 8: -1 9
w= 9: 9
w=10: 1 9
w=11: -1 3 9
w=12: 3 9
w=13: 1 3 9
w=14: -1 -3 -9 27
w=15: -3 -9 27
w=16: 1 -3 -9 27
w=17: -1 -9 27
w=18: -9 27
w=19: 1 -9 27
w=20: -1 3 -9 27
w=21: 3 -9 27
w=22: 1 3 -9 27
w=23: -1 -3 27
w=24: -3 27
w=25: 1 -3 27
w=26: -1 27
w=27: 27
w=28: 1 27
w=29: -1 3 27
w=30: 3 27
w=31: 1 3 27
w=32: -1 -3 9 27
w=33: -3 9 27
w=34: 1 -3 9 27
w=35: -1 9 27
w=36: 9 27
w=37: 1 9 27
w=38: -1 3 9 27
w=39: 3 9 27
w=40: 1 3 9 27
扩展:
1、砝码分盐问题。假设有 280g 盐,有一架天平,有两个砝码,分别是 4g 和 14g 。 能否在 3 次内将 280g 食盐分为 100g 和 180g 两堆,请详细描述你的解决方法。
2、分金条问题。你让工人为你工作7天,给工人的回报是一根金条。金条平分成相连的7段,你必须在每天结束时给他们一段金条,如果只许你两次把金条弄断,你如何给你 的工人付费。
参考资料:
1、http://blog.csdn.net/livelylittlefish/article/details/3854702

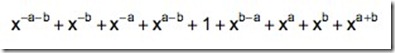
![MQMX{TRV@]J7(6@A4RZ`J}B MQMX{TRV@]J7(6@A4RZ`J}B](https://images.cnblogs.com/cnblogs_com/ttltry-air/201208/201208172031334048.jpg)
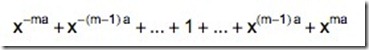
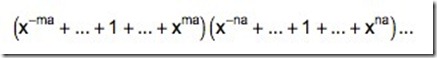
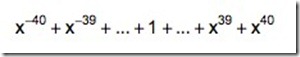
![DUA]1%LXWHTP{[G[`7]D{VN DUA]1%LXWHTP{[G[`7]D{VN](https://images.cnblogs.com/cnblogs_com/ttltry-air/201208/201208172031377556.jpg)
![%~E[E]OAJF((HXWPI{JR]1D %~E[E]OAJF((HXWPI{JR]1D](https://images.cnblogs.com/cnblogs_com/ttltry-air/201208/201208172031381360.jpg)
![A440A`PERV{D{2KI]M0CX4T A440A`PERV{D{2KI]M0CX4T](https://images.cnblogs.com/cnblogs_com/ttltry-air/201208/201208172031391228.jpg)

