BUUCTF---RSA1
- RSA基础概念
rsa原理: RSA公开密钥密码体制的原理是:根据数论,寻求两个大素数比较简单,而将它们的乘积进行因式分解却极其困难,因此可以将乘积公开作为加密密钥
RSA算法的具体描述如下:
(1)任意选取两个不同的大素数p和q计算乘积;
(2)任意选取一个大整数e,满足 ,整数e用做加密钥(注意:e的选取是很容易的,例如,所有大于p和q的素数都可用);
(3)确定的解密钥d,满足 ,即 是一个任意的整数;所以,若知道e和,则很容易计算出d ;
(4)公开整数n和e,秘密保存d [5];
(5)将明文m(m<n是一个整数)加密成密文c,加密算法为
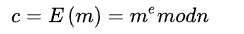
(6)将密文c解密为明文m,解密算法为
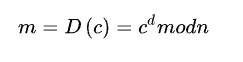
然而只根据n和e(注意:不是p和q)要计算出d是不可能的。因此,任何人都可对明文进行加密,但只有授权用户(知道d)才可对密文解密。
RSA会随着计算速度的提升而被逐步破解,量子计算机的出现会导致这种大素数攻击可实现
2.RSA1 由p,q,dp,dq,c求明文的算法
点击查看代码
import gmpy2
I = gmpy2.invert(q,p)
mp = pow(c,dp,p)
mq = pow(c,dq,q) #求幂取模运算
m = (((mp-mq)*I)%p)*q+mq #求明文公式
print(hex(m)) #转为十六进制
题目:
p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229
q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469
dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929
dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041
c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852
代码解决
点击查看代码
p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229
q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469
dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929
dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041
c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852
import gmpy2
import binascii
I = gmpy2.invert(q,p) #逆元 q-1
mp = pow(c,dp,p)
mq = pow(c,dq,q) #求幂取模运算
m = (((mp-mq)*I)%p)*q+mq #求明文公式
print(hex(m)) #转为十六进制
0x6e6f784354467b57333163306d335f37305f4368316e343730776e7d
十六进制转文本noxCTF{W31c0m3_70_Ch1n470wn}
本文作者:TTDB
本文链接:https://www.cnblogs.com/ttdb-huu/p/18268349
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步