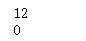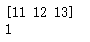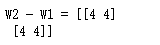import numpy as np
#构建一个含有一个常数12的0维张量
x = np.array(12)
print(x)
#ndim表示张量的维度
print(x.ndim)
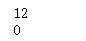
x1 = np.array([11,12,13])
print(x1)
print(x1.ndim)
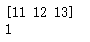
x2 = np.array([[11,12,13],[14,15,16]])
print(x2)
print(x2.ndim)

W1 = np.array([[1,2],[3,4]])
W2 = np.array([[5,6],[7,8]])
print("W2 - W1 = {0}".format(W2-W1))
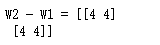
def matrix_multiply(x, y):
#确保第一个向量的列数等于第二个向量的行数
assert x.shape[1] == y.shape[0]
#一个m*d维的二维张量与一个d*n的二维张量做乘机后,得到m*n的二维张量
z = np.zeros((x.shape[0], y.shape[1]))
for i in range(x.shape[0]):
#循环第一个向量的每一行
for j in range(y.shape[1]):
#循环第二个向量的每一列
addSum = 0
for k in range(x.shape[1]):
addSum += x[i][k]*y[k][j]
z[i][j] = addSum
return z
x = np.array([[0.1, 0.3], [0.2,0.4]])
y = np.array([[1],[2]])
z = matrix_multiply(x, y)
print(z)


def naive_relu(x):
assert len(x.shape) == 2
x = x.copy() #确保操作不改变输入的x
for i in range(x.shape[0]):
for j in range(x.shape[1]):
x[i][j] = max(x[i][j], 0)
return x
x = np.array([[1, -1], [-2, 1]])
print(naive_relu(x))

x = np.array([
[
[1,2],
[3,4]
],
[
[5,6],
[7,8]
],
[
[9, 10],
[11, 12]
]
])
print(x.ndim)

from keras.datasets import mnist
(train_images, train_labels),(test_images, test_labels) = mnist.load_data()
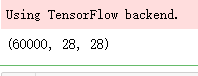
print(train_images.shape)
my_slice = train_images[10:100]
print(my_slice.shape)