|
|
|
|
|
|
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.neural_network import MLPClassifier
def creat_data(n):
'''
创建线性可分数据集
:param n: 正例样本的个数(同时也是负例样本的个数)
:return: 返回一个线性可分数据集,数据集大小为 2*n
'''
np.random.seed(1)
x_11=np.random.randint(0,100,(n,1)) # 第一组:第一维坐标值
x_12=np.random.randint(0,100,(n,1,))# 第一组:第二维坐标值
x_13=20+np.random.randint(0,10,(n,1,))#第一组: 第三维坐标值
x_21=np.random.randint(0,100,(n,1)) # 第二组:第一维坐标值
x_22=np.random.randint(0,100,(n,1)) # 第二组:第二维坐标值
x_23=10-np.random.randint(0,10,(n,1,)) # 第二组:第三维坐标值
new_x_12=x_12*np.sqrt(2)/2-x_13*np.sqrt(2)/2## 沿第一维轴旋转45度
new_x_13=x_12*np.sqrt(2)/2+x_13*np.sqrt(2)/2## 沿第一维轴旋转45度
new_x_22=x_22*np.sqrt(2)/2-x_23*np.sqrt(2)/2## 沿第一维轴旋转45度
new_x_23=x_22*np.sqrt(2)/2+x_23*np.sqrt(2)/2## 沿第一维轴旋转45度
plus_samples=np.hstack([x_11,new_x_12,new_x_13,np.ones((n,1))]) # 拼接成正例数据集
minus_samples=np.hstack([x_21,new_x_22,new_x_23,-np.ones((n,1))]) # 拼接成负例数据集
samples=np.vstack([plus_samples,minus_samples]) # 拼接成完整数据集
np.random.shuffle(samples) # 混洗数据
return samples
def creat_data_no_linear(n):
'''
创建线性不可分数据集
:param n: 正例样本的个数(同时也是负例样本的个数)
:return: 返回一个线性不可分数据集,数据集大小为 2*n
'''
np.random.seed(1)
x_11=np.random.randint(0,100,(n,1))# 第一组:第一维坐标值
x_12=np.random.randint(0,100,(n,1,))# 第一组:第二维坐标值
x_13=10+np.random.randint(0,10,(n,1,))#第一组: 第三维坐标值
x_21=np.random.randint(0,100,(n,1))# 第二组:第一维坐标值
x_22=np.random.randint(0,100,(n,1))# 第二组:第二维坐标值
x_23=20-np.random.randint(0,10,(n,1,)) # 第二组:第三维坐标值
new_x_12=x_12*np.sqrt(2)/2-x_13*np.sqrt(2)/2## 沿第一维轴旋转45度
new_x_13=x_12*np.sqrt(2)/2+x_13*np.sqrt(2)/2## 沿第一维轴旋转45度
new_x_22=x_22*np.sqrt(2)/2-x_23*np.sqrt(2)/2## 沿第一维轴旋转45度
new_x_23=x_22*np.sqrt(2)/2+x_23*np.sqrt(2)/2## 沿第一维轴旋转45度
plus_samples=np.hstack([x_11,new_x_12,new_x_13,np.ones((n,1))])# 拼接成正例数据集
minus_samples=np.hstack([x_21,new_x_22,new_x_23,-np.ones((n,1))])# 拼接成负例数据集
samples=np.vstack([plus_samples,minus_samples])# 拼接成完整数据集
np.random.shuffle(samples) # 混洗数据
return samples
def plot_samples(ax,samples):
'''
绘制样本点
:param ax: 绘制图形所在的 Axes
:param samples: 样本数据集
:return: None
'''
Y=samples[:,-1] # 标记信息
position_p=Y==1 ## 正类位置
position_m=Y==-1 ## 负类位置
# 绘制正类样本点
ax.scatter(samples[position_p,0],samples[position_p,1],samples[position_p,2],marker='+',label='+',color='b')
# 绘制负类样本点
ax.scatter(samples[position_m,0],samples[position_m,1],samples[position_m,2],marker='^',label='-',color='y')
def run_plot_samples():
'''
绘制线性可分数据集
:return: None
'''
fig=plt.figure()
ax=Axes3D(fig)
data=creat_data(100) # 产生线性可分数据集
plot_samples(ax,data)
ax.legend(loc='best')
plt.show()
run_plot_samples()

def run_plot_samples_no_linear():
'''
绘制线性不可分数据集
:return: None
'''
data=creat_data_no_linear(100)# 产生线性不可分数据集
fig=plt.figure()
ax=Axes3D(fig)
plot_samples(ax,data)
ax.legend(loc='best')
plt.show()
run_plot_samples_no_linear()
def perceptron(train_data,eta,w_0,b_0):
'''
感知机的原始算法
:param train_data: 训练数据集
:param eta: 学习率
:param w_0: 初始权重向量
:param b_0: 初始的 b
:return: 一个元组,依次为:最终的权重向量,最终的 b 值,迭代次数
'''
x=train_data[:,:-1] # x 数据
y=train_data[:,-1] # 对应的标记
length= train_data.shape[0] #样本集大小
w=w_0
b=b_0
step_num=0
while True:
i=0
while(i< length): ## 遍历一轮样本集中的所有的样本点
step_num+=1
'''
当应用于线性不可分数据集时,用下面4行代替上面的 step_num+=1 这一行。如果不这么做,那么当用于线性
不可分数据集时,迭代永远不会停止。
step_num+=1
if step_num>=10000000:
print("failed!,step_num =%d"%step_num)
return
'''
x_i=x[i].reshape((x.shape[1],1)) # 变成列向量,因为需要执行 np.dot 函数
y_i=y[i]
if y_i*(np.dot(np.transpose(w),x_i)+b) <=0: # 该点是误分类点
w=w+eta*y_i*x_i # 梯度下降
b=b+eta*y_i # 梯度下降
break # 执行下一轮筛选
else:#该点不是误分类点,选取下一个样本点
i=i+1
if(i== length): #没有误分类点,结束循环
break
return (w,b,step_num)
def creat_hyperplane(x,y,w,b):
'''
创建分离超平面
:param x: 分离超平面上的点的x坐标组成的数组
:param y: 分离超平面上的点的y坐标组成的数组
:param w: 超平面的法向量,它是一个列向量
:param b: 超平面的截距
:return: 分离超平面上的点的z坐标组成的数组
'''
return (-w[0][0]*x-w[1][0]*y-b)/w[2][0] # w0*x+w1*y+w2*z+b=0
def run_perceptron():
'''
对线性可分数据集执行感知机的原始算法并绘制分离超平面
'''
data=creat_data(100) #产生线性可分数据集
eta,w_0,b_0=0.1,np.ones((3,1),dtype=float),1 # 初始化 学习率、权重、 b
w,b,num=perceptron(data,eta,w_0,b_0) # 执行感知机的原始形式
### 绘图
fig=plt.figure()
plt.suptitle("perceptron")
ax=Axes3D(fig)
### 绘制样本点
plot_samples(ax,data)
## 绘制分离超平面
x=np.linspace(-30,100,100) # 分离超平面的 x坐标数组
y=np.linspace(-30,100,100) # 分离超平面的 y坐标数组
x,y=np.meshgrid(x,y) # 划分网格
z=creat_hyperplane(x,y,w,b) # 分离超平面的 z坐标数组
ax.plot_surface(x, y, z, rstride=1, cstride=1,color='g',alpha=0.2)
ax.legend(loc="best")
plt.show()
run_perceptron()

def perceptron_nolinear(train_data,eta,w_0,b_0):
'''
感知机的原始算法
:param train_data: 训练数据集
:param eta: 学习率
:param w_0: 初始权重向量
:param b_0: 初始的 b
:return: 一个元组,依次为:最终的权重向量,最终的 b 值,迭代次数
'''
x=train_data[:,:-1] # x 数据
y=train_data[:,-1] # 对应的标记
length= train_data.shape[0] #样本集大小
w=w_0
b=b_0
step_num=0
while True:
i=0
while(i< length): ## 遍历一轮样本集中的所有的样本点
step_num+=1
if step_num>=10000000:
print("failed!,step_num =%d"%step_num)
return
x_i=x[i].reshape((x.shape[1],1)) # 变成列向量,因为需要执行 np.dot 函数
y_i=y[i]
if y_i*(np.dot(np.transpose(w),x_i)+b) <=0: # 该点是误分类点
w=w+eta*y_i*x_i # 梯度下降
b=b+eta*y_i # 梯度下降
break # 执行下一轮筛选
else:#该点不是误分类点,选取下一个样本点
i=i+1
if(i== length): #没有误分类点,结束循环
break
return (w,b,step_num)
def creat_hyperplane(x,y,w,b):
'''
创建分离超平面
:param x: 分离超平面上的点的x坐标组成的数组
:param y: 分离超平面上的点的y坐标组成的数组
:param w: 超平面的法向量,它是一个列向量
:param b: 超平面的截距
:return: 分离超平面上的点的z坐标组成的数组
'''
return (-w[0][0]*x-w[1][0]*y-b)/w[2][0] # w0*x+w1*y+w2*z+b=0
def run_perceptron_no_linear():
'''
对线性不可分数据集执行感知机的元素算法
'''
data=creat_data_no_linear(100)#产生线性不可分数据集
perceptron_nolinear(data,eta=0.1,w_0=np.zeros((3,1)),b_0=0)
run_perceptron_no_linear()

def creat_w(train_data,alpha):
'''
根据训练数据集和 alpha向量 创建 权重向量
:param train_data: 训练数据集
:param alpha: alpha 向量
:return: 权重向量
'''
x=train_data[:,:-1] # x 数据
y=train_data[:,-1] # 对应的分类
N= train_data.shape[0] #样本集大小
w=np.zeros((x.shape[1],1))
for i in range(0,N):
w=w+alpha[i][0]*y[i]*(x[i].reshape(x[i].size,1))
return w
def perceptron_dual(train_data,eta,alpha_0,b_0):
'''
感知机的对偶形式算法
:param train_data: 训练数据集
:param eta: 学习率
:param alpha_0: 初始的 alpha 向量
:param b_0: 初始的 b 值
:return: 一个元组,依次为:最终的alpha 向量、最终的 b 值、迭代次数
'''
x=train_data[:,:-1] # x 数据
y=train_data[:,-1] # 对应的分类
length= train_data.shape[0] #样本集大小
alpha=alpha_0
b=b_0
step_num=0
while True:
i=0
while(i< length):
step_num+=1
x_i=x[i].reshape((x.shape[1],1)) # 变形为列向量,因为需要调用 np.dot
y_i=y[i]
w=creat_w(train_data,alpha)
z=y_i*(np.dot(np.transpose(w),x_i)+b)
if z <=0: # 该点是误分类点
alpha[i][0]+=eta # 梯度下降
b+=eta*y_i # 梯度下降
break # 梯度下降了,从头开始,执行下一轮筛选
else:
i=i+1 #该点不是误分类点,选取下一个样本点
if(i== length ): #没有误分类点,结束循环
break
return (alpha,b,step_num)
def run_perceptron_dual():
'''
对线性可分数据集执行感知机的原始算法和对偶形式算法,并绘制分离超平面
'''
data=creat_data(100)
eta,w_0,b_0=0.1,np.ones((3,1),dtype=float),1
w_1,b_1,num_1=perceptron(data,eta,w_0,b_0) ##执行原始形式的算法
alpha,b_2,num_2=perceptron_dual(data,eta=0.1,alpha_0=np.zeros((data.shape[0]*2,1)),
b_0=0) # 执行对偶形式的算法
w_2=creat_w(data,alpha)
print("w_1,b_1",w_1,b_1)
print("w_2,b_2",w_2,b_2)
## 绘图
fig=plt.figure()
plt.suptitle("perceptron")
ax=Axes3D(fig)
### 绘制样本点
plot_samples(ax,data)
## 绘制分离超平面
x=np.linspace(-30,100,100) # 分离超平面的 x坐标数组
y=np.linspace(-30,100,100) # 分离超平面的 y坐标数组
x,y=np.meshgrid(x,y) # 划分网格
z=creat_hyperplane(x,y,w_1,b_1) # 原始形式算法的分离超平面的 z坐标数组
z_2=creat_hyperplane(x,y,w_2,b_2) # 对偶形式算法的分离超平面的 z坐标数组
ax.plot_surface(x, y, z, rstride=1, cstride=1,color='g',alpha=0.2)
ax.plot_surface(x, y, z_2, rstride=1, cstride=1,color='c',alpha=0.2)
ax.legend(loc="best")
plt.show()
run_perceptron_dual()

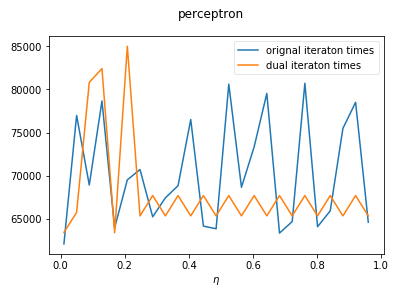
def test_eta(data,ax,etas,w_0,alpha_0,b_0):
'''
测试学习率对于感知机两种形式算法的收敛速度的影响
:param data: 训练数据集
:param ax: Axes实例,负责绘制图形
:param etas: 候选的学习率的值组成的列表
:param w_0: 原始算法用到的初始权重向量
:param alpha_0: 对偶形式用到的初始 alpha 向量
:param b_0: 初始 b 值
:return: None
'''
nums1=[]
nums2=[]
for eta in etas:
_,_,num_1=perceptron(data,eta,w_0=w_0,b_0=b_0) # 获取原始形式算法的迭代次数
_,_,num_2=perceptron_dual(data,eta=0.1,alpha_0=alpha_0,b_0=b_0) # 获取对偶形式算法的迭代次数
nums1.append(num_1)
nums2.append(num_2)
ax.plot(etas,np.array(nums1),label='orignal iteraton times')
ax.plot(etas,np.array(nums2),label='dual iteraton times')
def run_test_eta():
fig=plt.figure()
fig.suptitle("perceptron")
ax=fig.add_subplot(1,1,1)
ax.set_xlabel(r'$\eta$')
data=creat_data(20) # 创建线性可分数据集
etas=np.linspace(0.01,1,num=25,endpoint=False)
w_0,b_0,alpha_0=np.ones((3,1)),0,np.zeros((data.shape[0],1))
test_eta(data,ax,etas,w_0,alpha_0,b_0)
ax.legend(loc="best",framealpha=0.5)
plt.show()
run_test_eta()
发表于
2019-05-01 12:55
吴裕雄
阅读( 424)
评论()
编辑
收藏
举报
|
|








