百面机器学习笔记-1

特征工程

　　特征归一化

　　为了消除数据特征之间的量纲影响，我们需要对特征进行归一化处理，使得 不同指标之间具有可比性。想要得到更为准确的结果，就需要进行特征归一化 （Normalization）处理，使各指标处于同一数值量级，以便进行分析。

　　question：为什么需要对数值类型的特征做归一化？

　　answer：对数值类型的特征做归一化可以将所有的特征都统一到一个大致相同的数值 区间内。其中线性函数归一化（Min-Max Scaling）：将原始数据进行线性变换，使结果映射到【0，1】的范围，实现对原始数据的等比缩放,公式：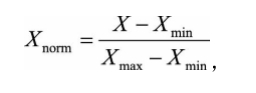

其中X为原始数据，，Xmax、Xmin分别为数据最大值和最小值。零均值归一化（Z-Score Normalization）：将原始数据映射为均值为0，标准差为1的分布上。公式为：

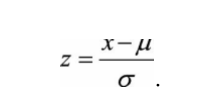
特征均值为μ、标准差为σ。

　　为什么需要对数值型特征做归一化呢？我们不妨借助随机梯度下降的实例来 说明归一化的重要性。假设有两种数值型特征，x1的取值范围为 [0, 10]，x2的取值 范围为[0, 3]，于是可以构造一个目标函数符合图1.1（a）中的等值图。 在学习速率相同的情况下，x1的更新速度会大于x2，需要较多的迭代才能找到 最优解。如果将x1和x2归一化到相同的数值区间后，优化目标的等值图会变成图 1.1（b）中的圆形，x1和x2的更新速度变得更为一致，容易更快地通过梯度下降找 到最优解。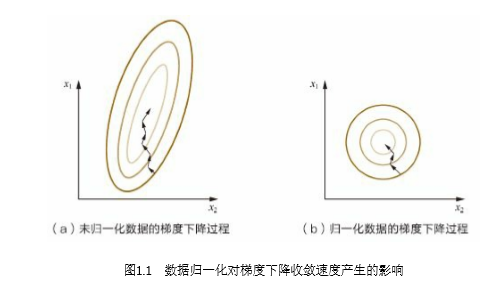

在实际应用中，通过梯度下降法求解的模 型通常是需要归一化的，包括线性回归、逻辑回归、支持向量机、神经网络等模 型。但对于决策树模型则并不适用。

　　类别型特征

　　类别型特征（Categorical Feature）主要是指性别（男、女）、血型（A、B、 AB、O）等只在有限选项内取值的特征。类别型特征原始输入通常是字符串形 式，除了决策树等少数模型能直接处理字符串形式的输入，对于逻辑回归、支持 向量机等模型来说，类别型特征必须经过处理转换成数值型特征才能正确工作。

　　question:在对数据进行预处理时，应该怎样处理类别型特征？

　　answer：

　　　　　1. 序号编码：序号编码通常用于处理类别间具有大小关系的数据。例如成绩，可以分为 低、中、高三档，并且存在“高>中>低”的排序关系。序号编码会按照大小关系对 类别型特征赋予一个数值ID，例如高表示为3、中表示为2、低表示为1，转换后依 然保留了大小关系。

　　　　　　2. 独热编码：独热编码通常用于处理类别间不具有大小关系的特征。例如血型，一共有4个 取值（A型血、B型血、AB型血、O型血），独热编码会把血型变成一个4维稀疏 向量，A型血表示为（1, 0, 0, 0），B型血表示为（0, 1, 0, 0），AB型表示为（0, 0, 1, 0），O型血表示为（0, 0, 0, 1）。对于类别取值较多的情况下使用独热编码需要 注意以下问题。

　　　　　　　　（1）使用稀疏向量来节省空间。在独热编码下，特征向量只有某一维取值为 1，其他位置取值均为0。因此可以利用向量的稀疏表示有效地节省空间，并且目前大部分的算法均接受稀疏向量形式的输入。

　　　　　　　　（2）配合特征选择来降低维度。高维度特征会带来几方面的问题。一是在K 近邻算法中，高维空间下两点之间的距离很难得到有效的衡量；二是在逻辑回归 模型中，参数的数量会随着维度的增高而增加，容易引起过拟合问题；三是通常 只有部分维度是对分类、预测有帮助，因此可以考虑配合特征选择来降低维度。

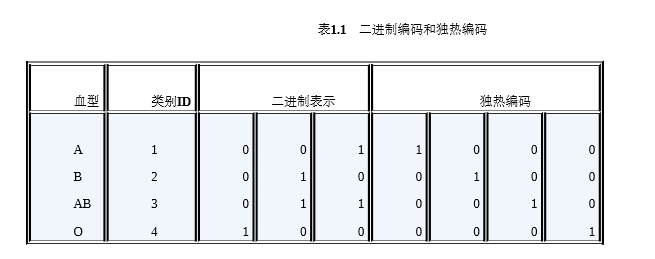
　　　　　　3. 二进制编码：二进制编码主要分为两步，先用序号编码给每个类别赋予一个类别ID，然后 将类别ID对应的二进制编码作为结果。以A、B、AB、O血型为例，表1.1是二进制 编码的过程。A型血的ID为1，二进制表示为001；B型血的ID为2，二进制表示为 010；以此类推可以得到AB型血和O型血的二进制表示。可以看出，二进制编码本 质上是利用二进制对ID进行哈希映射，最终得到0/1特征向量，且维数少于独热编 码，节省了存储空间。

　　高维组合特征的处理

　　question:什么是组合特征？如何处理高维组合特征？

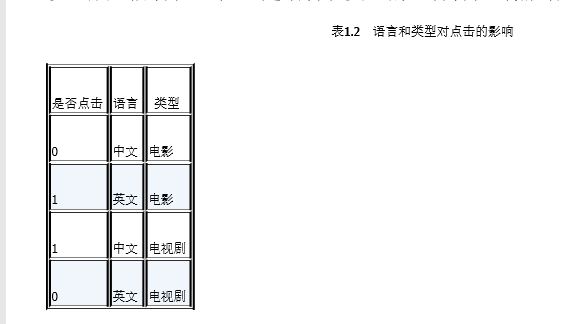
　　answer：为了提高复杂关系的拟合能力，在特征工程中经常会把一阶离散特征两两组 合，构成高阶组合特征。以广告点击预估问题为例，原始数据有语言和类型两种 离散特征，表1.2是语言和类型对点击的影响。为了提高拟合能力，语言和类型可 以组成二阶特征，表1.3是语言和类型的组合特征对点击的影响。

以逻辑回归为例，假设数据的特征向量为X=(x1,x2,...,xk)，则有其中<xi, xj>表示xi和xj的组合特征，wij的维度等于|xi|·|xj|，|xi|和|xj|分别代表第i个特征 和第j个特征不同取值的个数。在表1.3的广告点击预测问题中，w的维度是 2×2=4（语言取值为中文或英文两种、类型的取值为电影或电视剧两种）。这种特 征组合看起来是没有任何问题的，但当引入ID类型的特征时，问题就出现了。以 推荐问题为例:  若用户的数量为m、物品的数量为n，那么需要学习的参数的规模为m×n。在 互联网环境下，用户数量和物品数量都可以达到千万量级，几乎无法学习m×n规模 的参数。在这种情况下，一种行之有效的方法是将用户和物品分别用k维的低维向 量表示（k<<m,k<<n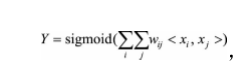）其中 ， 和 分别表示xi和xj对应的低维向量。推荐问题 中，需要学习的参数的规模变为m×k+n×k。熟悉推荐算法的同学很快可以看出来， 这其实等价于矩阵分解。所以，这里也提供了另一个理解推荐系统中矩阵分解的 思路。

　　组合特征

　　question：怎么有效的找到组合特征？

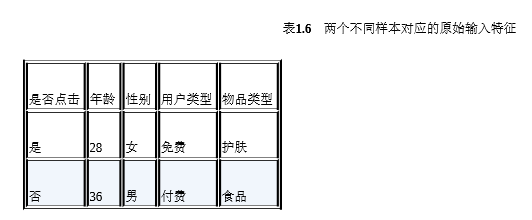
　　answer：以点击预测问题为例，假设原始输入特征包含年龄、性别、用户 类型（试用期、付费）、物品类型（护肤、食品等）4个方面的信息，并且根据原 始输入和标签（点击/未点击）构造出了决策树，如图1.2所示。于是，每一条从根节点到叶节点的路径都可以看成一种特征组合的方式。具 体来说，就有以下4种特征组合的方式。

（1）“年龄<=35”且“性别=女”。

（2）“年龄<=35”且“物品类别=护肤”。

（3）“用户类型=付费”且“物品类型=食品”。

（4）“用户类型=付费”且“年龄<=40”。

　　

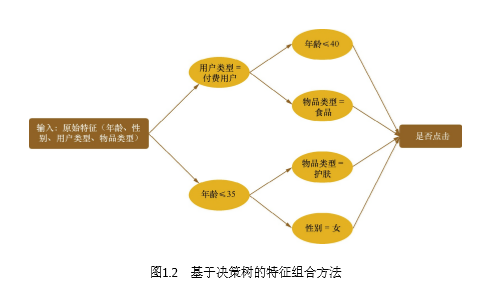
表1.6是两个样本信息，那么第1个样本按照上述4个特征组合就可以编码为 （1, 1, 0, 0），因为同时满足（1）（2），但不满足（3）（4）。同理，第2个样 本可以编码为（0, 0, 1, 1），因为它同时满足（3）（4），不满足（1）（2）。

给定原始输入该如何有效地构造决策树呢？可以采用梯度提升决策树，该方 法的思想是每次都在之前构建的决策树的残差上构建下一棵决策树。